 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение термина наибольшего и наименьшего значения функции 12
Наибольшим значением функции у=f(x) на промежутке X называют такое значение Наименьшим значением функции y=f(x) на промежутке X называют такое значение Эти определения понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на данном интервале при абсциссе t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>0</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 2.2 Алгоритм нахождения наибольшего и наименьшего значений функции f(x) на непрерывном отрезке 1) Найти производную 2) Найти стационарные и критические точки функции, лежащие на отрезке 3) Вычислить значения функции y= f(x) в точках, отобранных на втором шаге, и в точках a и b: выбрать среди этих значений наименьшее и наибольшее.
Производная функции Определение производной функции: Производной функции f в точке
Экстремум функции Пусть Определение 1. Число М называется локальным максимумом функции Определение 2. Число m называется локальным минимумом функции Определение 3. Локальный максимум и локальный минимум называются локальными экстремумами. Соответствующая точка Теорема Ферма. Если функция Определение 4. Точки, в которых производная функции равна нулю, называются стационарными точками. Замечание. Функция может иметь экстремум и в точке, где эта функция не имеет производной. Например, Определение 5. Точки, в которых функция имеет производную, равную нулю, или не является дифференцируемой, называют критическими точками. Для того, чтобы точка Теорема 1. (достаточные условия того, что стационарная точка является точкой экстремума) Пусть функция 1) если при переходе через точку 2) если при переходе через точку Теорема 2. (достаточные условия того, что стационарная точка является точкой экстремума) Пусть функция 1) если 2) если Схема для решения задач на определение экстремума функций. 1. Установить область определения функции 2. Найти её первую производную. 3. Найти стационарные точки функции 4. Определить знак производной на числовых интервалах, на которые стационарные и критические точки разбили область определения. Практическая часть Рассмотрим теперь на практике, какие бывают задачи и как можно исследовать функцию на наибольшее и наименьшее значение. Задача №1 Укажите наибольшее число, принадлежащее промежутку а) [-15; -11]; б) [5; 7); в) [5; 7]. Так же в 7 классе а теме «Линейная функция» Мордкович А.Г. вводит само понятие наибольшего и наименьшего значения функции на отрезке. Он рассматривает линейную функцию y на отрезке [0;6].
Рис. 1 Соответствующий отрезок графика выделяется на чертеже. Замечается, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 - это и есть наибольшее значение заданной линейной функции на отрезке. Записывается это следующим образом Задача №2 Постройте график функции а) значения у при х = 4; 7; 16; б) значения х, если у = 0; 1; 3; в) наименьшее и наибольшее значения функции на отрезке [0; 4]; г) при каких значениях х график функции расположен выше прямой у = 1; ниже прямой у = 1. Найдите наименьшее и наибольшее значения функции а) на отрезке [0; 4]; б) на луче в) на отрезке [1; 9]; г) на полуинтервале (2; 9]. Постройте график функции а) значения у при х = -3; 1; 6; б) значения х если у = 3; -1; -6; в) наименьшее и наибольшее значения функции на отрезке [-3; -1]; Решите двойное неравенство Найдите наименьшее целое число, удовлетворяющее системе неравенств
Задача №3 Определить наибольшее и наименьшее значение функции на промежутке. 1. Функция определена на всем множестве действительных чисел
Найдем производную функции
Приравняем ее к нулю и определим критические точки
Проверим знак производной слева и справа от найденной точки
Производная при переходе через точку
Найдем значение функции в точке
и на краях отрезка
Таким образом, функция достигает максимума в точке локального экстремума
Задача №4
На заданном промежутке функция определена; вычислим ее производную
Приравнивая нуля найдем критическую точку
Заданная точка принадлежит отрезку. Найдем значения функции во всех точках
Функция приобретает максимум и минимум в точках
Задача №5
Функция определена везде, потому приступим сразу к вычислению производной
Приравняем ее к нулю и находим критические точки
Найдем значения функции во всех подозрительных на экстремум точках
Из полученного набора значений следует, что функция принимает максимум и минимум на краях отрезка
Задача №6 Найти наибольшее и наименьшее значение функции Решение. Находим производную функции:
Находим точки, в которых производная равна нулю:
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку [0;5]. Оба значения лежат в этом промежутке. Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка: y(0)=4; y( Таким образом,
Ответ: Задача №7 Найти наибольшее и наименьшее значения функции Решение: В этой задаче используется теорема о том, что непрерывная функция достигает своего наибольшего и наименьшего значений на отрезке: либо в критических точках, где производная обращается в нуль или не существует; либо на концах отрезка. Таким образом, для того, чтобы найти наибольшее и наименьшее значения функции на данном отрезке, необходимо найти её значения в критических точках и на концах отрезка, а затем сравнить эти значения. Перепишем выражение функции в виде: Найдем производную функции в виде: Найдем критические точки:
Сравнивая полученные значения, можем заключить, что наибольшее значение равно Ответ: Наибольшее значение функции на отрезке равно Наименьшее значение функции на отрезке равно
Задача №9 С помощью производных высших порядков найти экстремум функции Решение: Находим производную функции:
Находим Значит Значит
Задача №9 Найдите наименьшее значение функции (0; 2) Решение: 1. 2. 3. На интервале (0; 2) данная функция непрерывна, имеет единственный экстремум в точке x=1 и этот экстремум - минимум. Следовательно, Ответ: 1
Задача №10 Основание пирамиды - равнобедренный прямоугольный треугольник. Все боковые рёбра пирамиды равны Решение: Примем высоту DO данной пирамиды за x, где ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> На интервале (0;
Следовательно, V(1)= Ответ: Замечание: Рассмотренный выше алгоритм нахождения наибольшего (наименьшего) значения функции на интервале применим и для нахождения наибольшего (наименьшего) значения функции на отрезке, если функция непрерывна на этом отрезке и имеет на нём единственный экстремум.
Задача №12 Найдите наименьшее значение функции
Решение:
Задача №12 Найдите наименьшее значение функции Решение: Напомним, что любая функция принимает наименьшее или наибольшее значение тогда, когда ее производная равна нулю или не существует. Найдем производную
Видим, что производная равна нулю при x1=0 и x2=5 Заметим, что при х ∈ [4; 5) производная y´(x)<0 и значит функция убывает при х ∈ (5; 6] производная y´(x)>0 и значит функция возрастает То есть при х = 5 y´(x) меняет знак с - на +, значит при х = 5 наименьшее значение: у(5) = (52 - 7*5 + 7) * е5-5 = (25 - 35 + 7) * е0 = -3*1 = -3. Ответ: -3. Задача №14 Найти наибольшее и наименьшее значение функции r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Решение: Поскольку + - +
Отсюда видно, что наименьшее значение Поскольку Ответ: Задача №15 Найдите наибольшее значение функции Решение: Напомним, что любая функция принимает наименьшее или наибольшее значение тогда, когда ее производная равна нулю или не существует. Найдем производную
Заметим, что
Делаем такой вывод: так как производная
Подставим
Ответ: 7. Задача № 16 Найдите наибольшее значение площади прямоугольника со сторонами параллельными осям координат, и с диагональю OP, где О – начало координат, а Р – точка на графике функции Решение: Длины сторон прямоугольника равны положительным координатам точки Р. Поэтому его площадь равна их произведению:
Так как Так как Ответ: 13.
Заключение Над изучением этой темы работали многие ученые и философы. Много лет назад появились такие термины как функция, график, исследование функции и до сих пор они сохранились, приобретая новые черты и признаки. Я выбрала эту тему, потому что мне было очень интересно узнать историю возникновения исследования функции. Мне кажется, что многим было бы интересно побольше узнать о функции, о ее свойствах и преобразованиях. Сделав эту курсовую работу, я систематизировала свои навыки пополнила свой запас знаний об этой теме.
Список используемой литературы
1. Мордкович А.Г. Алгебра и начала математического анализа 10-11кл. – Москва, 2009. 2. Мордкович А.Г. и др. Задачник по алгебре и началам математического анализа 10-11кл. – Москва,2009. 3. Колмогоров А.Н., Абрамов А.М. и др. Алгебра и начала математического анализа 10-11кл. – Просвещение, 2008. 4. Башмаков М.И. Алгебра и начала анализа 10-11 кл. – Москва, 1992. 5. Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа 10-11кл. – Москва, 2010. 6. Виленкин Н.Я. Производная и задачи на экстремум // Квант,1978 №6 с. 60-64. 7. Гусак А. А.. Высшая математика. Учебное пособие для студентов вузов в 2-х томах. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.). 8. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с. 9. Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000 г. 10. Ткачук В.В. Математика абитуриенту М: МЦНМО, 2008.
12 |
= f( 
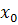), что для любого x 
, x≠ 
= f(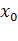 
), , что для любого x 
, x≠t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>0</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
.
(x).
, при 
, стремящемся к нулю.
- область определения функции 
и точка 
.
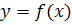, если существует такая окрестность точки 
из нее выполняется неравенство 
. При этом М= 
, а сама точка 
. При этом m= 
- точка минимума функции 
, а 
не существует.
, 
- стационарная точка функции 
слева от точки 
справа от точки 
, - стационарная точка функции 
, то 
, то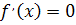 
, и точки, в которых 
не определена.
. Далее отмечается, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке части прямой, равна 4 - это и есть наименьшее значение линейной функции на отрезке [0; 6]. Записывают так 
.
. С помощью графика найдите:
. С помощью графика найдите:
и укажите наименьшее и наибольшее целые числа, которые являются его решениями.
.
;
.
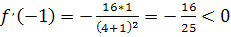
и минимума на одном из краев отрезка 
.
.
.
.
.
.
.
; 
.
.
.
;
.
;
;
;
.
; 
.
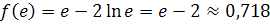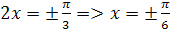на отрезке [0;5].
)= 
3,92; y(5)=454
; 
.
на заданном отрезке 
.
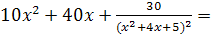. Отсюда 
10 или 
.
, а наименьшее значение равно s New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>=-5</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
.
.
. Найдем критические точки: s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>cosx</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math" w:cs="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>=0</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
,
;
;
, вычисляем 
,
– точки минимума функции; 
,
– точки максимума функции.
на интервале
;
;
- наименьшее значение данной функции на интервале (0; 2)
. Найдите наибольший возможный объём такой пирамиды.
. Из прямоугольного треугольника ADO находим AO2=3-x2 , а из равнобедренного треугольника ACO находим AC2=2AO2 =2(3-x2) . Таким образом, требуется найти наибольшее значение функции V(x)= 
на интервале (0; 
; 
;
- наибольшее значение данной функции на интервале (0; 
На множестве (-3; 2] имеем: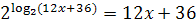 
; 
Следовательно, 
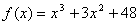Таким образом, требуется найти наименьшее значение функции 
. Решим уравнение 
на множестве(-3; 2]: 
Функция r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
, заданная на множестве R, возрастает на отрезке [-3; -2], следовательно, для любого 
выполняется условие 
. Значения функций g(x) и f(x) совпадают на множестве (-3; 2], значит, для любого 
. На отрезке [-2;2] функция f(x) непрерывна, имеет единственный экстремум и этот экстремум - минимум. Следовательно, 
- наименьшее значение функции f(x) на отрезке [-2; 2]. Таким образом, число 48 - наименьшее значение функции f(x).
на отрезке s w:ascii="Cambria Math" w:h-ansi="Cambria Math" w:cs="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:spacing w:val="-20"/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:bidi="AR-SA"/></w:rPr><m:t>4;6</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">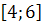 
.
и приравняем ее к нулю.
на отрезке 
.
, критические точки f(x) совпадают с теми, для которых производная равна нулю. Легко найти, что это точки 
. Из того, что 
, следует, что знак 
, и можно нарисовать картинку поведения f(x) на отрезке 
принимает либо в точке -2, либо в точке 1.
, наименьшее значение функции на отрезке 
и 
. Поскольку 
, наибольшее значение 
; 
.
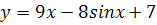на отрезке 
.
.
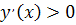при любых 
, как мы знаем, это выполнимо всегда, так как 
.
, то функция возрастает на этом отрезке и наибольшее значение будет при наибольшем x их этого отрезка - это 
и получим 
, так как 
.
.
. Исследуем функцию 
, 
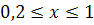с помощью производной.
.
, а по условию 
– единственная критическая точка. Найдем значения функции S в концах отрезка [0,2; 1] и сравним их с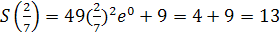 
.
, то 
. Так как 
, то 
, 
, и 
.