 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение макроскопических сечений среды.
В этом разделе находим макроскопические сечения реакций поглощения
При условии теплового равновесия со средой в ячейке устанавливается спектр тепловых нейтронов, называемый спектром Максвелла с температурой нейтронного газа
3.3.1. Определение макроскопических сечений производим по формуле:
где:
Сечения поглощения тепловых нейтронов в справочнике [2] приведены для энергии
3.3.1.1. Для
3.3.1.2. Для
3.3.1.3. Для
3.3.1.4. Для
3.3.1.5. Для С:
3.3.2. Определение замедляющей способности среды:
где Найдем среднелогарифмическую потерю энергии:
Результаты запишем в таблицу 1:
Таблица 1.
3.3.3. Найдем температуру нейтронного газа
где
Макроскопические сечения поглощения при температуре замедлителя
Согласно рекомендациям [2, стр. 9], принимаем температуру нейтронного газа
Наиболее вероятная энергия тепловых нейтронов
Спектр замедляющихся нейтронов переходит в спектр тепловых при энергии
Усредненные по спектру Максвелла сечения для большинства элементов находим по формуле:
Следуя рекомендациям [2, стр. 9-10] определили
Отсюда,
Функция
В качестве примера определим усредненное по спектру Максвелла сечение для циркония:
Для остальных элементов блока
3.3.4. Для учета гетерогенности разобьем ячейку на две зоны: блок и замедлитель.
3.3.4.1. Объем блока:
3.3.4.2. Объем замедлителя:
3.3.4.3. Радиус блока:
3.3.4.4. Радиус замедлителя:
3.3.4.5. Усредненные по блоку концентрации элементов находим по формуле:
3.3.4.6. Определим замедляющую способность:
3.3.4.7. Транспортные сечения находим по формуле:
где,
В качестве примера расчета:
Для воды транспортное сечение, усредненное по спектру Максвелла вычислим по формуле:
Для блока составим таблицу 2.
Таблица 2.
Используя данные таблицы 2, находим:
Для второй зоны ячейки примем параметры чистого графита. Тогда два штриха указываю, что величина вычислена во второй зоне. Расчеты производим аналогичным по расчету для блока методом и так же сведем в таблицу 3.
Таблица 3.
3.3.4.8. Коэффициент диффузии тепловых нейтронов в блоке:
3.3.4.9. Коэффициент длины диффузии:
3.3.4.10. Обратная длина диффузии:
3.3.4.11. Коэффициент диффузии тепловых нейтронов в замедлителе:
3.3.4.12. Коэффициент длины диффузии в замедлителе:
3.3.4.13. Обратная длина диффузии:
3.3.4.14. Отношение плотностей потока тепловых нейтронов в двух зонах найдем, используя решение уравнения диффузии:
где,
|



 , замедляющую способность среды
, замедляющую способность среды  , транспортное макроскопическое сечение
, транспортное макроскопическое сечение 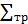 и сечение деления
и сечение деления  .
.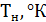 . Для усреднений сечений по спектру Максвелла необходимо определить температуру нейтронного газа.
. Для усреднений сечений по спектру Максвелла необходимо определить температуру нейтронного газа.
 микроскопическое сечение поглощения элемента, вещества см. Справочник [2];
микроскопическое сечение поглощения элемента, вещества см. Справочник [2]; средняя по гомогенной ячейке концентрация элемента.
средняя по гомогенной ячейке концентрация элемента. , что соответствует температуре
, что соответствует температуре  , а микроскопические сечения рассеяния
, а микроскопические сечения рассеяния  считаем независимыми от энергии и равными их значениям при
считаем независимыми от энергии и равными их значениям при  .
. :
:
 :
:
 :
:
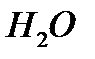 :
:


 микроскопические сечения рассеяния взяты из справочника [2].
микроскопические сечения рассеяния взяты из справочника [2].




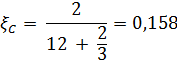



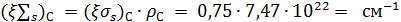







 , барн
, барн

 , барн
, барн






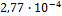
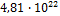



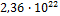








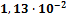



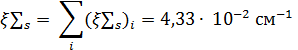
 температура замедлителя (средняя по объему активной зоны). Согласно рекомендациям [1, стр. 89] получим,
температура замедлителя (средняя по объему активной зоны). Согласно рекомендациям [1, стр. 89] получим,

 оценим в предположении зависимости
оценим в предположении зависимости 

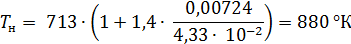


 постоянная Больцмана
постоянная Больцмана
 , называемой граничной энергией тепловой группы или энергией сшивки спектров Ферми и Максвелла.
, называемой граничной энергией тепловой группы или энергией сшивки спектров Ферми и Максвелла.



 [2, стр. 24]
[2, стр. 24]

 приведены в таблице 2
приведены в таблице 2


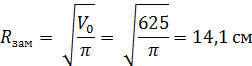



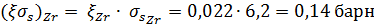

 средний косинус угла рассеяния
средний косинус угла рассеяния














 , барн
, барн
 , барн
, барн

 , барн
, барн




 ,
, 

 ,
,  ,
, 

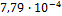



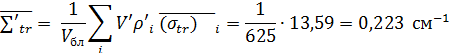




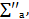


 ,
,  ,
,  ,
, 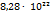








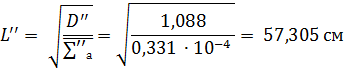



 отношение мощностей источников тепловых нейтронов в обеих зонах:
отношение мощностей источников тепловых нейтронов в обеих зонах:
 функции Бесселя мнимого аргумента
функции Бесселя мнимого аргумента


