 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пользуясь данными таблицы, составить расчетную схему электрической цепи 12
При составлении расчетной схемы учитываются ее параметры, указанные в задании, т.е. на схеме показываются только те источники питания, которые предусмотрены таблицей вариантов: источники ЭДС заменяются перемычками, если Е = 0, а источники тока разрывом, если J= 0. При расчете схемы внутренние сопротивления источников ЭДС принять равными нулю, т.е. полагать источники идеальными. Источники тока J и включенные параллельно с ними сопротивления rпар. следует заменить эквивалентными источниками ЭДС E с внутренними сопротивлениями rвн., используя формулы эквивалентного преобразования
Рисунок. 2 E = Jrпар. rвн. = rпар.
Рисунок. 3
Уравнения контурных токов имеют вид:
Где:
Подставляем значения в систему:
Составляются определители контурных уравнений: основной
 1, 1,  2, 2,  3 . 3 .
По найденным определителям вычисляются контурные токи:
I11 =
I33 = По контурным токам определяются токи в ветвях цепи:
I1 = -I11 = -3,202А; I2 = I11 - I22 = 3,202 – 0.951 = 2,251 А; I3 = I33- I11 = 1,887-3,202=-1,315А; I4 = I22= 0,951 А; I5 = I22 -I33= 0,951 – 1,887 = - 0,936 А; I6 =- I33 = -1,887 А. Записать систему уравнений Кирхгофа, необходимых для определения токов во всех ветвях схемы и выполнить проверку расчета цепи методом контурных токов На схеме (рис. 3) указываются направления токов I 1, I2, I3, I4 , I5, I6 в ветвях с учетом их знаков и направлений контурных токов и составляются узловые уравнения по первому закону Кирхгофа для независимых узлов 1, 2, и 3. Число независимых уравнений на единицу меньше общего числа узлов в цепи. -I1 – I2 – I4 = 0; I2 + I3 + I5 = 0; I4 + I6 – I5 = 0.
Выбираются независимые контуры и произвольно принимаются направления их обхода; для всех контуров по второму закону Кирхгофа составляются контурные уравнения. -I1 R1 + I2 R2 – I3 R3 = E1 + E2; -I2 R2 + I4 R4 + I5 R5 =- E2 +E4; I3 R3 -I5 R5 - I6 R6 = 0. -I1 R1 + I2 R2 – I3 R3 =3,202x7+2,251x4+1,315x5=22,414+9,004+6,575= 37,993 В E1 + E2=18+20=38 В -I2 R2 + I4 R4 + I5 R5= -2,251х4+0,951х4-0,936х3=-9,004+3,804-2,808=-8,008 В - E2 +E4=-20+12=-8 В I3 R3 -I5 R5 - I6 R6=-1,315х5+0,936х3+1,887х2=-6,575+2,808+3,774=0.007 В Выделить в схеме три сопротивления, включенные по схеме треугольника, и заменить их эквивалентным соединением по схеме звезды
Рисунок. 4 На рис. 4 указано, что треугольником соединены сопротивления R1; R2; R3. Сопротивления эквивалентного соединения в звезду имеют значения: R12 = R1 R2/ (R1 + R2 + R3) = 28/16=1,75 Ом; R13 = R1 R3/( R1 + R2 + R3 ) = 35/16=2,19 Ом; R23 = R2 R3/(R1 + R2 + R3) =20/16= 1,25 Ом;
Рисунок. 5
Рисунок. 5 Для определения напряжения UАВ составляется уравнение по второму закону Кирхгофа для замкнутого контура, который показан штриховой линией на рис. 5 UАВ – I1R1 – I3 R3 + Е2 = 0 Из этого уравнения находится UАВ UАВ = - Е2+ I1 R1 + I3 R3 = -20 +22,414 +6,575 = 8,989 В. 12 |



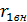
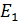
























 =7+4+5=16 Ом
=7+4+5=16 Ом =4+4+3=11 Ом
=4+4+3=11 Ом =5+3+2=10 Ом
=5+3+2=10 Ом =4 Ом
=4 Ом  =5 Ом
=5 Ом  =3 Ом
=3 Ом =18+20=38 В
=18+20=38 В  =-20+12=-8 В
=-20+12=-8 В  =0 В
=0 В


 и дополнительные
и дополнительные =16×11×10+−4×−3×−5+−5×−4×−3−5×11×−5−−3×−3×16−10×−4×−4=1061
=16×11×10+−4×−3×−5+−5×−4×−3−5×11×−5−−3×−3×16−10×−4×−4=1061 =38×11×10+−4×−3×0+−5×−8×−3−0×11×−5−−3×−3×38−10×−8×−4=3398
=38×11×10+−4×−3×0+−5×−8×−3−0×11×−5−−3×−3×38−10×−8×−4=3398 =16×−8×10+38×−3×−5+−5×−4×0−−5×−8×−5−0×−3×16−10×−4×38=1010
=16×−8×10+38×−3×−5+−5×−4×0−−5×−8×−5−0×−3×16−10×−4×38=1010 =16×11×0+−4×−8×−5+38×−4×−3−−5×11×38−−3×−8×16−0×−4×−4=2002
=16×11×0+−4×−8×−5+38×−4×−3−−5×11×38−−3×−8×16−0×−4×−4=2002