 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчет добротности полюсов
ВВЕДЕНИЕ Активные фильтры занимают особое место в современных радиотехнических системах. Важнейшими преимуществами активных фильтров являются их высокие технические характеристики, сочетающиеся с простотой проектирования и наладки, а также с хорошими массогабаритными показателями, в особенностипосравнению с пассивными RLC-фильтрами. В области рабочих частот от долей герца до сотен килогерц и небольшихмощностей активные фильтры находятся вне конкуренции с любыми другими видами фильтров в связи с возможностью применения в их конструкции операционных усилителей. На более высоких частотах широко используются активныефильтры, выполненных на базе дискретных усилительных электронных приборов,несмотря на то, что расчет таких фильтров значительно сложнее, так как требуетточного учета частотных характеристик применяемых усилительных приборов. Особенно актуальными становятся вопросы проектирования аналоговых активных фильтров в связи с развитием цифровых средств передачи и обработкиинформации. Характеристики аналоговых фильтров, устанавливаемых в точкахпреобразования аналоговых сигналов в цифровые или цифровых сигналов в аналоговые, существенно определяют качество работы всей системы в целом. ОСНОВЫ ПОСТРОЕНИЯ ФИЛЬТРОВ Электрический фильтр – это четырехполюсник, имеющий неравномерную амплитудно-частотную характеристику. Полосу частот, в которой сигналы проходят со входа на выход четырехполюсника с малым затуханием, называют полоса пропускания или полоса прозрачности, или зона прозрачности. Полосу частот, в которой сигналы проходят со входа на выход четырехполюсника с большим затуханием, называют полоса задерживания ил полоса затухания. Частотные характеристики фильтров часто идеализируют, считая, что в полосе пропускания амплитудно-частотная характеристика постоянна |Н(jw)|=const, затухание A(w)=a мало, а в полосе задерживания затухание бесконечно велико.
Рисунок 1 – АЧХ идеализированного фильтра низких частот. Идеальные фильтры физически нереализуемы, на практике следует учитывать наличие переходных областей между полосами прозрачности и задерживания. Кроме того, необходимо принимать во внимание, что, во-первых, затухание входного сигнала в полосе задерживания всегда является конечным, а во-вторых, в полосе прозрачности возможны колебания или плавное изменение затухания. На практике часто возникает необходимость в фильтрах с более плоским участком характеристики в полосе пропускания и более крутыми склонами. Такая потребность существует всегда, когда надо отфильтровать сигнал от близкой по частоте помехи. Немедленно возникает следующий очевидный вопрос: можно ли (соединяя каскадно-одинаковые фильтры, скажем, нижних частот), получить аппроксимацию идеальной характеристики фильтра нижних частот типа «кирпичная стена», как это показано на рис.1. Известно, что простое каскадное соединение не дает результата без ухудшения общей характеристики, так как входное сопротивление каждого звена будет служить существенной нагрузкой для предыдущего звена. Но если поставить буферы между всеми звеньями (или сделать полное входное сопротивление каждого звена намного выше, чем у предыдущего) то, казалось бы, можно добиться желаемого эффекта. Тем не менее ответ на поставленный вопрос будет отрицательным. Соединенные каскадноRС-фильтры действительно дадут суммарную характеристику с крутым наклоном, но «излом» этой амплитудно-частотной характеристики не будет резким. Это можно сформулировать так: из многих плавных перегибов не сделать одного крутого. Обычно считают, что граничная частота между полосой пропускания и полосой задерживания равна единице. Такого рода частотная характеристика называется нормированной относительно частоты среза. Кроме того, на рисунках принят логарифмический масштаб оси частоты. Затухание также изображается в логарифмическом масштабе
При использовании в качестве элемента схемы фильтра ОУ можно синтезировать характеристику любого RLC-фильтра без применения катушек индуктивности. Такие безиндуктивные фильтры известны под названием «активные фильтры». В соответствии с названием, активный фильтр - это электрический фильтр, в состав которого входит активный усилительный элемент. Таким элементом может являться операционный усилитель, усилительный каскад, собранный на полупроводниковых транзисторах или электронных лампах. Тип активного элемента выбирается в зависимости от того, в каком диапазоне частот должен функционировать активный фильтр. Важнейшей особенностью активных фильтров является возможность каскадного проектирования.
Рисунок 2 – Каскадное соединение звеньев фильтра. Усилитель в составе активного фильтра выбирается таким образом, чтобы взаимовлияние последующего предыдущего каскадов друг на друга было минимальным, рисунок 2. Передаточную функцию фильтра в целом можно достаточно точно определить, как произведение передаточных функций отдельных звеньев:
число звеньев ограничено себестоимостью фильтра, сложностью технологической настройки параметров фильтра. На практике встречаются фильтры с числом звеньев от одного до нескольких десятков. Помимо возможности физической реализуемости необходимо, чтобы передаточная функция фильтра отвечала еще одному важнейшему требованию. Вид передаточной функции должен быть легко соотносим с заданными техническими характеристикам проектируемого фильтра. Другими словами, важно знать, как, задаваясь теми или иными техническими требованиями, определять количество коэффициентов числителя и знаменателя передаточной функции, как вычислять сами коэффициенты. Технические требования к фильтру могут быть сформулированы различными способами. Характерные частоты обычно указывают в герцах. Часто расчетные формулы подразумевают подстановку частоты в радианах в секунду: ФИЛЬТР НИЖНИХ ЧАСТОТ
Рисунок 3–технические требования к полосно-пропускающему фильтру. Для проектирования ФНЧ устанавливают следующие исходные данные:
Термин максимально допустимое затухание сигнала в полосе прозрачности следует понимать таким образом, что на любой частоте в границах полосы прозрачности затухание сигнала не должно превышать заданный предел. Это означает также, что в границах полосы прозрачности коэффициент передачи не будет опускаться ниже соответствующего значения. Аналогично понимают термин минимально допустимое затухание в полосе задерживания. Затухание всех сигналов с частотами в границах полосы задерживания не должно быть менее указанного предела. Соответственно, коэффициент передачи в полосе задерживания не должен превышать заданную величину. В ряде случаев указывают дополнительные требования к виду амплитудночастотной характеристики в полосе прозрачности. Это связано с тем, что реализация некоторых видов фильтров приводит к различным сложным формам АЧХ. В полосе прозрачности и в полосе задерживания могут иметь место пульсации коэффициента передачи. Тогда в технических требованиях указывают:
ФИЛЬТР БАТТЕРВОРТА Амплитудно-частотная характеристика фильтра Баттерворта является наиболее плоской в полосе пропускания из всех рассматриваемых фильтров. Однако, крутизна спада характеристики в переходной полосе невелика. В полосе задерживания АЧХ фильтра также равномерно спадает. На рисунке 2 показано семейство АЧХ фильтров Баттерворта разного порядка.
Рисунок 2– АЧХ фильтра Баттерворта разных порядков ЗАДАНИЕ Спроектировать активный фильтр с заданными характеристиками: Тип фильтра: Фильтр Полосно-пропускающий; Вид фильтра: Фильтр Чебышевв; Граничная частота полосы пропускания: 31 Гц; Граничная частота полосы задержания: 67 Гц; Неравномерность ЧХ в полосе пропускания: 1,9 дБ; Минимальное затухание в полосе задержания: 42 дБ; РАСЧЕТНАЯ ЧАСТЬ Расчет порядка фильтра
Подставив значения
Выбираем из таблицы передаточную функцию фильтра прототипа:
Т. к. проектируем ФНЧ фильтр, требуется выполнить масштабирование частоты:
Расчетполюсовфильтра Расчет полюсов проводим по формуле:
Подставивзначения,получим:
Расчет добротности полюсов Расчет добротности полюсов проводим по формуле:
где
Расчетчастотполюсов Расчет частот полюсов проводим по формуле:
где
Переводим частоты в Герцы по формуле:
Мы имеем фильтр нижних частот с одной цепью первого порядка, и тремя цепями второго порядка.
|







 . Значения коэффициента передачи удобнее задавать в децибелах. На частотах, на которых коэффициент передачи меньше единицы, его выражение в децибелах становиться отрицательным числом. Единичный коэффициент передачи соответствует 0 дБ. Затухание также задается в децибелах и показывает, как ослабляется сигнал.
. Значения коэффициента передачи удобнее задавать в децибелах. На частотах, на которых коэффициент передачи меньше единицы, его выражение в децибелах становиться отрицательным числом. Единичный коэффициент передачи соответствует 0 дБ. Затухание также задается в децибелах и показывает, как ослабляется сигнал.




 получим:
получим:











 ‒координата полюса по мнимой оси,
‒координата полюса по мнимой оси,  ‒ координата полюса по вещественной оси.
‒ координата полюса по вещественной оси.

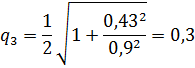
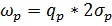
 ‒ добротность полюса,
‒ добротность полюса, 





