 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Классификация методов математического моделирования
ОГЛАВЛЕНИЕ с
ВВЕДЕНИЕ
Объекты материального мира сложны и многообразны. Отражение всех их свойств в создаваемых, изучаемых и используемых образах весьма затруднительно, да и не нужно. Важно, чтобы образ объекта содержал черты, наиболее важные для его использования Методом моделирования называется замена объекта оригинала объектом-заместителем, обладающим определенным сходством с оригиналом, с целью получения новой информации об оригинале. Моделью называется объект-заместитель объекта-оригинала, предназначенный для получения информации об оригинале. Математические модели относятся к символьным моделям и представляют собой описание объектов в виде математических символов, формул, выражений. При наличии достаточно точной математической модели можно путем математических расчетов прогнозировать результаты функционирования объекта при различных условиях, выбрать из множества возможных вариантов тот, который дает наилучшие результаты. В данной работе приведены виды классификации математических методов моделирования и описаны некоторые методы: - Линейное программирование - это методы математического моделирования, которые служат для поиска оптимального варианта распределения ограниченных ресурсов между конкурирующими работами. -Имитационное моделирование. Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между её элементами или другими словами — разработке симулятора исследуемой предметной области для проведения различных экспериментов.
Классификация методов математического моделирования Ввиду разнообразия применяемых математических моделей, их общая классификация затруднена. В литературе обычно приводят классификации, в основу которых положены различные подходы и принципы. По принадлежности к иерархическому уровню математические модели делятся на модели микроуровня, макроуровня, метауровня. Математические модели на микроуровне процесса отражают физические процессы, протекающие, например, при резании металлов. Они описывают процессы на уровне перехода (прохода). Математические модели на макроуровне процесса описывают технологические процессы. Математические модели на метауровне процесса описывают технологические системы (участки, цехи, предприятие в целом). По характеру отображаемых свойств объекта модели можно классифицировать на структурные и функциональные Модель структурная, – если она представима структурой данных или структурами данных и отношениями между ними В свою очередь, структурная модель может быть иерархической или сетевой. Модель иерархическая (древовидная), – если представима некоторой иерархической структурой (деревом); например, для решения задачи нахождения маршрута в дереве поиска можно построить древовидную модель, приведенную на рисунке 1.
Рисунок 1 - Модель иерархической структуры. Модель сетевая, – если она представима некоторой сетевой структурой. Например, строительство нового дома включает различные операции которые можно представить в виде сетевой модели, приведенной на рисунке 2.
Рисунок 2 - Модель сетевой структуры.
Модель функциональная, – если она представима в виде системы функциональных соотношений. Например, закон Ньютона и модель производства товаров –функциональные. По способу представления свойств объекта модели делятся на аналитические, численные, алгоритмические и имитационные. Аналитические математические модели представляют собой явные математические выражения выходных параметров как функций от параметров входных и внутренних и имеют единственные решения при любых начальных условиях. Например, процесс резания (точения) с точки зрения действующих сил представляет собой аналитическую модель. Также квадратное уравнение, имеющее одно или несколько решений, будет аналитической моделью. Модель будет численной, если она имеет решения при конкретных начальных условиях (дифференциальные, интегральные уравнения). Модель алгоритмическая, если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим ее функционирование и развитие. Введение данного типа моделей (действительно, кажется, что любая модель может быть представлена алгоритмом её исследования) вполне обосновано, т. к. не все модели могут быть исследованы или реализованы алгоритмически. Например, моделью вычисления суммы бесконечного убывающего ряда чисел может служить алгоритм вычисления конечной суммы ряда до некоторой заданной степени точности. Алгоритмической моделью корня квадратного из числа Х может служить алгоритм вычисления его приближенного, сколь угодно точного значения по известной рекуррентной формуле. Модель имитационная, – если она предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели, например модель экономической системы производства товаров двух видов. Такую модель можно использовать в качестве имитационной с целью определения и варьирования общей стоимости в зависимости от тех или иных значений объемов производимых товаров. По способу получения модели делятся на теоретические и эмпирические Теоретические математические модели создаются в результате исследования объектов (процессов) на теоретическом уровне. Например, существуют выражения для сил резания, полученные на основе обобщения физических законов. Но они неприемлемы для практического использования, т. к. очень громоздки и не совсем адаптированы к реальным процессам. Эмпирические математические модели создаются в результате проведения экспериментов (изучения внешних проявлений свойств объекта с помощью измерения его параметров на входе и выходе) и обработки их результатов методами математической статистики. По форме представления свойств объекта модели делятся на логические, теоретико-множественные и графовые. Модель логическая, если она представима предикатами, логическими функциями, например, совокупность двух логических функций может служить математической моделью одноразрядного сумматора. Модель теоретико-множественная, если она представима с помощью некоторых множеств и отношений принадлежности к ним и между ними. Модель графовая, – если она представима графом или графами и отношениями между ними. По степени устойчивости. модели могут быть разделены на устойчивые и неустойчивые. Устойчивой является такая система, которая, будучи выведена из своего исходного состояния, стремится к нему. Она может колебаться некоторое время около исходной точки, подобно обычному маятнику, приведенному в движение, но возмущения в ней со временем затухают и исчезают В неустойчивой системе, находящейся первоначально в состоянии покоя, возникшее возмущение усиливается, вызывая увеличение значений соответствующих переменных или их колебания с возрастающей амплитудой По отношению к внешним факторам модели могут быть разделены на открытые и замкнутые. Замкнутой моделью является модель ,которая функционирует вне связи с внешними (экзогенными) переменными. В замкнутой модели изменения значений переменных во времени определяются внутренним взаимодействием самих переменных. Замкнутая модель может выявить поведение системы без ввода внешней переменной. Пример: информационные системы с обратной связью являются замкнутыми системами. Это самонастраивающиеся системы, и их характеристики вытекают из внутренней структуры и взаимодействий, которые отражают ввод внешней информации. Модель, связанная с внешними (экзогенными) переменными, называется открытой. По отношению к временному фактору модели делятся на динамические и статические Модель называется статической, если среди параметров, участвующих в ее описании, нет временного параметра. Динамической моделью называется модель, если среди ее параметров есть временной параметр, т. е. она отображает систему (процессы в системе) во времени. одновременно. Линейное программирование
Среди задач математического программирования самыми простыми (и лучше всего изученными) являются так называемые задачи линейного программирования. Характерно для них то, что: а) показатель эффективности (целевая функция) W линейно зависит от элементов решения х1, х2, ....., хп и б) ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно х1, х2, ..., хп Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т. д. Это и естественно, так как во многих задачах практики «расходы» и «доходы» линейно зависят от количества закупленных или утилизированных средств (например, суммарная стоимость партии товаров линейно зависит от количества закупленных единиц; оплата перевозок производится пропорционально весам перевозимых грузов и т. д.). Любую задачу линейного программирования можно свести к стандартной форме, так называемой «основной задаче линейного программирования» (ОЗЛИ), которая формулируется так: найти неотрицательные значения переменных х1 ,х2, ..., хп, которые удовлетворяли бы условиям-равенствам (1).
и обращали бы в максимум линейную функцию этих переменных (2):
Случай, когда f надо обратить не в максимум, а в. минимум, легко сводится к предыдущему, если попросту изменить знак f на обратный (максимизировать не f, а f' = - f). Кроме того, от любых условий-неравенств можно перейти к условиям-равенствам ценой введения новых дополнительных переменных. В зависимости от вида целевой функции и ограничений можно выделить несколько типов задач линейного программирования или линейных моделей: общая линейная задача, транспортная задача, задача о назначениях. Транспортная задача (задача Монжа - Канторовича) - математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки. Задача о назначениях формулируется следующим образом: Имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами. Если число работ и исполнителей совпадает, то задача называется линейной задачей о назначениях. Существует несколько способов решения задачи линейного программирования, в частности графический метод и симплекс-метод. Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется для решения задач двумерного пространства. Задачи трёхмерного пространства решаются очень редко, т.к. построение их решения неудобно и лишено наглядности. Рассмотрим метод на примере двумерной задачи.
Найти решение Х = (х1,х2), удовлетворяющее системе неравенств (3)
x1-x2 ≥-3
2x1-3x2≤6 x1+ x2≥4 x1, x2 ≥0
при котором значение целевой функции F = 2x1x2 достигает максимума. Построим на плоскости в декартовой прямоугольной системе координат х1Ох2 область допустимых решений задачи. Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой нет. Чтобы определить искомую полуплоскость нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей и проверить: удовлетворяют ли её координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка. В противном случае другая полуплоскость. Найдём полуплоскость, определяемую неравенством x1-x2 ≥-3. Для этого, построив прямую (I) x1-x2 =-3, возьмём какую-нибудь точку, принадлежащую одной из двух полученных полуплоскостей, например, точку O(0,0). Координаты этой точки удовлетворяют неравенству x1-x2 ≥-3. Значит полуплоскость, которой принадлежит точка O(0,0) определяется неравенством x1-x2 ≥-3. Теперь найдём полуплоскость, определяемую неравенством 6x1+7x2≤42. Строим прямую II 6x1+7x2=42. Координаты точки O(0,0) удовлетворяют неравенству6x1+7x2≤42, а значит, искомой будет вторая полуплоскость. Теперь ищем полуплоскость для неравенства 2 x1-3 x2≤6. Координаты точки O(0,0) удовлетворяют неравенств 2 x1-3 x2≤6. Следовательно, полуплоскость, которой принадлежит точка O(0,0) определяется неравенством 2 x1-3 x2≤6 (Прямая III). И полуплоскость для неравенства x1+ x2≥4. Координаты точки О(0,0) удовлетворяют неравенству x1+ x2≥4 (Прямая IV). Отсюда прямая x1+ x2=4 определяется первой полуплоскостью. Неравенства x1≥0 и x2≥0 означают, что область решения будет расположена справа от оси ординат и над осью абсцисс. Таким образом, заштрихованная на рисунке 3 область ABCD будет областью допустимых решений, определённой ограничениями задачи . Целевая функция принимает свое максимальное значение в одной из вершин фигуры ABCD. Для определения этой вершины, построим вектор С (2; -1) и прямую 2x1-x2=р, где pнекоторая постоянная такая, что прямая2x1-x2=p имеет общие точки с многоугольником решений. Положим, например, p=1/2 и построим прямую 2 x1-x2 =1/2. Далее, будем передвигать построенную прямую в направлении вектора На рисунке 3 видно, что последней общей точкой прямой 2x1-x2=p с многоугольником решений является точка A. Эта точка является местом пересечения прямой II и III, поэтому ее координаты
2x1-3x2=6
При этом значение целевой функции F = 2 x1-x2= 2* 5.25 – 1 *1.5 = 9. Точка B будет оптимальным решением задачи Хопт = (х1опт, х2опт) и ее координаты будут равны х1опт =5.25, х2 опт =1.5.
Рисунок 3 - Область допустимых решений задачи Симплекс - метод Данный метод является методом целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует. Основное содержание симплексного метода заключается в следующем: 1) Указать способ нахождения оптимального опорного решения. 2) Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения. 3) Задать критерии, которые позволяют своевременно прекратить перебор опорных решений на оптимальном решении или сделать заключение об отсутствии оптимального решения[4, с.40]. Для того, чтобы решить задачу симплексным методом необходимо выполнить следующее: 1) Привести задачу к каноническому виду. 2) Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решения ввиду несовместимости системы ограничений). 3) Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода. 4) Если выполняется признак единственности оптимального решения, то решение задачи заканчивается. Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения. Вычислительная эффективность математических методов оценивается обычно при помощи двух параметров: 1) Числа итераций, необходимого для получения решения; 2) Затрат машинного времени. В результате численных экспериментов получены результаты для симплекс-метода: 1) Число итераций при решении задач линейного программирования в стандартной форме с 2) Требуемое машинное время пропорционально Число ограничений больше влияет на вычислительную эффективность, чем число переменных, поэтому при формулировке задач линейного программирования нужно стремиться к уменьшению числа ограничений пусть даже путём роста числа переменных.
Основные понятия метода имитационного моделирования.
Под термином «имитационное моделирование» («имитационная модель») обычно подразумевают вычисление значений некоторых характеристик развивающегося во времени процесса путем воспроизведения течения этого процесса на компьютере с помощью его математической модели, причем получить требуемые результаты другими способами или невозможно, или крайне затруднительно. Воспроизведение течения процесса на компьютере с помощью математической модели принято называть имитационным экспериментом. Имитационные модели относятся к классу моделей, которые являются системой соотношений между характеристиками описываемого процесса. Эти характеристики разделяют на внутренние («эндогенные», «фазовые переменные») и внешние («экзогенные», «параметры»). Приблизительно внутренние характеристики — это те, значения которых намереваются узнать с помощью средств математического моделирования; внешние — такие, от которых внутренние характеристики существенно зависят, но обратная зависимость (с практически приемлемой точностью) не имеет места. Модель, способная давать прогноз значений внутренних характеристик, должна быть замкнутой («замкнутая модель»), в том смысле, что ее соотношения позволяют вычислять внутренние характеристики при известных внешних. Процедура определения внешних характеристик модели называется ее идентификацией, или калибровкой. Математические модели описанного класса (к ним относят имитационные модели) определяют отображение, позволяющее получить по известным значениям внешних характеристик значения внутренних. Далее это отображение будет называться отображением, ассоциированным с моделью. В основе моделей рассматриваемого класса лежит постулат о независимости внешних характеристик от внутренних, а соотношения модели являются формой записи ассоциированного с ней отображения. Как показано на рисунке 4 в процессе имитационного моделирования исследователь имеет дело с четырьмя основными элементами:• - реальная система; - логико-математическая модель моделируемого объекта; - имитационная (машинная) модель; - ЭВМ, на которой осуществляется имитация – направленный вычислительный эксперимент. Исследователь изучает реальную систему, разрабатывает логико-математическую модель реальной системы. Имитационный характер исследования предполагает наличие логико или логико-математических моделей, описываемых изучаемый процесс. Выше, реальная система определялась как совокупность взаимодействующих элементов, функционирующих во времени. Составной характер сложной системы описывает представление ее модели в виде трех множеств:A, S, T, где
Рисунок 4 Процесс имитационного моделирования
Особенностью имитационного моделирования является то, что имитационная модель позволяет воспроизводить моделируемые объекты: - с сохранением их логической структуры; -с сохранением поведенческих свойств (последовательности чередования во времени событий, происходящих в системе), т.е. динамики взаимодействий. При имитационном моделировании структура моделируемой системы адекватно отображается в модели, а процессы ее функционирования проигрываются (имитируются) на построенной модели. Поэтому построение имитационной модели заключается в описании структуры и процессов функционирования моделируемого объекта или системы. Различают имитационные модели: - непрерывные; - дискретные; - непрерывно-дискретные. В непрерывных имитационных моделях переменные изменяются непрерывно, состояние моделируемой системы меняется как непрерывная функция времени, и, как правило, это изменение описывается системами дифференциальных уравнений. Соответственно продвижение модельного времени зависит от численных методов решения дифференциальных уравнений. В дискретных имитационных моделях переменные изменяются дискретно в определенные моменты имитационного времени (наступления событий). Динамика дискретных моделей представляет собой процесс перехода от момента наступления очередного события к моменту наступления следующего события. Поскольку в реальных системах непрерывные и дискретные процессы часто невозможно разделить, были разработаны непрерывно-дискретные модели, в которых совмещаются механизмы продвижения времени, характерные для этих двух процессов. Метод имитационного моделирования позволяет решать задачи высокой сложности, обеспечивает имитацию сложных и многообразных процессов, с большим количеством элементов. Отдельные функциональные зависимости в таких моделях могут описываться громоздкими математическими соотношениями. Поэтому имитационное моделирование эффективно используется в задачах исследования систем со сложной структурой с целью решения конкретных проблем. Имитационная модель содержит элементы непрерывного и дискретного действия, поэтому применяется для исследования динамических систем, когда требуется анализ узких мест, исследование динамики функционирования, когда желательно наблюдать на имитационной модели ход процесса в течение определенного времени. Имитационное моделирование - эффективный аппарат исследования стохастических систем, когда исследуемая система может быть подвержена влиянию многочисленных случайных факторов сложной природы. Имеется возможность проводить исследование в условиях неопределенности, при неполных и неточных данных. Имитационное моделирование является важным фактором в системах поддержки принятия решений, т.к. позволяет исследовать большое число альтернатив (вариантов решений), проигрывать различные сценарии при любых входных данных. Главное преимущество имитационного моделирования состоит в том, что исследователь для проверки новых стратегий и принятия решений, при изучении возможных ситуаций, всегда может получить ответ на вопрос “Что будет, если?”. Имитационная модель позволяет прогнозировать, когда речь идет о проектируемой системе или исследуются процессы развития (т.е. в тех случаях, когда реальной системы еще не существует). В имитационной модели может быть обеспечен различный, в том числе и высокий уровень детализации моделируемых процессов. При этом модель создается поэтапно, эволюционно.
СПИСОК ЛИТЕРАТУРЫ
1. Блинов, Ю.Ф. Методы математического моделирования [Текст] : Электронное учебное пособие / Ю.Ф. Блинов, В.В. Иванцов, П.В. Серба. –Таганрог : ТТИ ЮФУ, 2012. –42 с. 2. Вентцель, Е.С. Исследование операций. Задачи, принципы, методология. [Текст] : Учебное пособие / Е.С. Вентцель - М. : КНОРУС, 2010. - 192 с. 3. Гетманчук, А. В. Экономико-математические методы и модели [Текст]: Учебное пособие для бакалавров. / А.В. Гетманчук - М. : Издательско-торговая корпорация «Дашков и Ко», 2013. —188 с. 4. Замятина, О.М. Моделирование систем. [Текст] : Учебное пособие. / О.М. Замятина – Томск : Изд-во ТПУ, 2009. – 204 с. 5. Павловский, Ю.Н. Имитационное моделирование. [Текст] : учебное пособие для студентов ВУЗов / Ю.Н.Павловский, Н.В.Белотелов, Ю.И.Бродский - М. : Издательский центр «Академия», 2008. – 236 с.
|







 , до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.
, до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи. находятся как решение системы уравнений, задающих эти прямые:
находятся как решение системы уравнений, задающих эти прямые:

 ограничениями и
ограничениями и  переменными заключено между
переменными заключено между 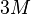 . Среднее число итераций
. Среднее число итераций  . Верхняя граница числа итераций равна
. Верхняя граница числа итераций равна  .
. .
.