 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вычислить коэффициенты регрессии.
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
1. Реалистичное содержание целевой функции В качестве целевой функции (функции отклика, зависимой переменной, реакции системы на воздействие факторов Xi) Y принята прокаливаемость (мм):
Y = f(Х1, Х2, Х3).
2. Реалистичное содержание (сущность) факторов
В качестве факторов функции отклика Xi принимаются:
X1 - температура закалки, °С. X2 - содержание углерода, % Х3 - содержание хрома, %
Уровни варьирования значений факторов
Минимальные и максимальные значения факторов приняты следующие:
Среднее значение фактора Среднее значение фактора определяется по формуле:
X10 =; X20 =; X30 =.
Интервалы варьирования фактора Интервал варьирования определяется по формуле:
dx1 = X1max-X10 = dx2 = X2max-X20= dx3 = X3max-X30=
Корректность определения значений факторов
Нормированные значения факторов Нормированные значения определяются формулой:
Хн1 = Хн2 = Хн3=
8. Матрица планирования полного факторного эксперимента Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен и равен 1.
Экспериментальные значения целевой функции
Дисперсия среднего арифметического для каждой строки матрицы эксперимента (каждого опыта) Дисперсия среднего арифметического определяется формулой:
где m – количество параллельных опытов в строке матриц.
Расчетное значение критерия Кохрена Критерий Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них, и определяется по формуле:
где S2max – наибольшая величина дисперсии результатов опыта; si – дисперсия i-го опыта$ N – общее число опытов в матрице. Максимальное значение дисперсии результатов опыта:
S2ymax= Сумма всех построчных дисперсий:
Расчетное значение критерия Кохрена:
Gp=
В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N , где N – число опытов (количество строк в матрице планирования). Табличное значение критерия Кохрена Уровень значимости.
a = 0,05
Степень числителя (f1):
f1= m –1= 5-1=4
где m – количество параллельных опытов в строке матриц
Степень свободы знаменателя (f2):
f2 = N = 8
где N – общее число опытов в матрице. Табличное значение критерия Кохрена
Gт = 0,4251 Оценка однородности дисперсии результатов опыта.
Так как расчётное значение Gp, которое равно 0,421288515, меньше табличного значения Gт, которое равно 0,4251, то соблюдается условие:
Gт > Gp ,
Следовательно все построчные дисперсии являются однородными.
Вид уравнения регрессии, принятого для построения модели функции отклика
Рекомендуется полиномиальная модель функции отклика
y = b0 X0 + b1 X1 + b2 X2 + b3 X3 +b12 X1Х2+b13 X1Х3+b23 X2Х3+b123 X1 X2Х3.
Вычислить коэффициенты регрессии. Значения коэффициентов регрессии определяются по формулам:
и так далее для всех коэффициентов.
Таблица - Значения коэффициентов регрессии.
|



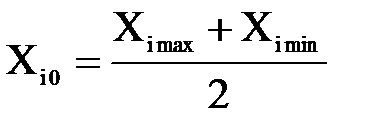 .
. .
.

 S2 y =
S2 y =
 ;
; 