ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчет температурного поля в многослойной конструкции
Определим температуры на границах слоёв многослойной конструкции наружной стены, тепловой поток и глубина промерзания при следующих данных:
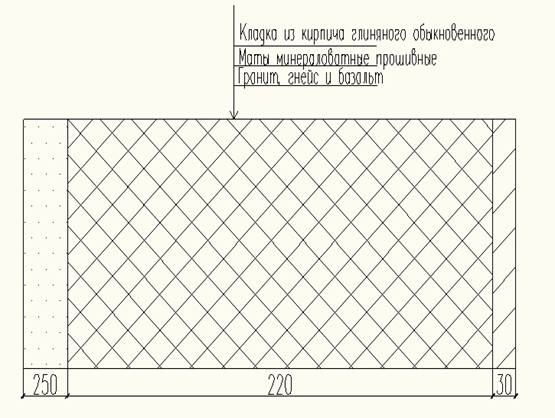
Рисунок 2.1 – Наружная стена здания
- Кладка из кирпича глиняного обыкновенного(Д) λ 1 = 0,81 Вт/( м ∙°С); S1 = 10,12 Вт/(м2 ∙°С); - Маты минераловатные прошивные (А) λ 2 = 0,07 Вт/( м ∙°С); S2 = 0,73Вт/(м2 ∙°С); - Гранит, гнейс и базальт (В) λ 3 = 1,28Вт/( м ∙°С); S3 = 9,91 Вт/(м2 ∙°С);
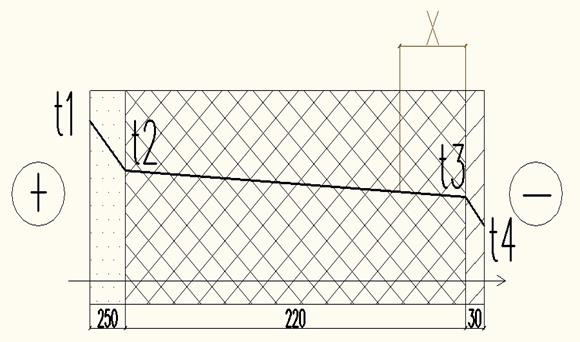
Рисунок 2.2 – Изменение температуры в наружной стене
Определяем термическое сопротивление каждого слоя материала: Для определения тепловой инерции стены находим термическое сопротивление отдельных слоев конструкции по формуле:
где δ – толщина рассматриваемого слоя, м ; λ – коэффициент теплопроводности данного слоя, Вт/(м∙°С). Вычислим термическое сопротивление отдельных слоев:
- Кладка из кирпича глиняного обыкновенного
- Маты минераловатные прошивные
- Гранит, гнейс и базальт
Вот тут Штирлиц чего-то не понял. А принимали, вроде, Определим тепловой поток через трехслойную конструкцию при разности температур двух сред:
где tв - температура внутреннего воздуха, °С; tн - температура наружного воздуха, °С . Определяем температуры на границах слоев конструкции по формуле:
где tx - температура в любой точке конструкции, °С; Rx - часть термического сопротивления, находящегося между плоскостями c температурами t1 и tx, (м2 ∙ ºС)/Вт.
Граница промерзания находится в слое «маты минераловатные прошивные». Определяем глубину промерзания в теплоизоляционном слое и составляем пропорцию:
Отсюда х=0,06 м;
Общая глубина промерзания в этом случае составит: δпр = х+0,03=0,09м.
Рисунок 2.2 – Глубина промерзания в теплоизоляционном слое
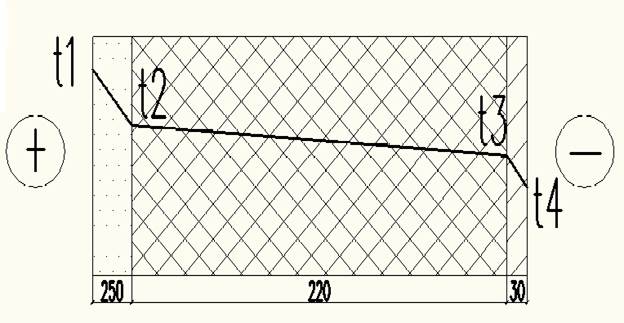
Рассмотрим данную задачу в случае, когда температура наружного и внутреннего воздуха поменяны друг с другом .
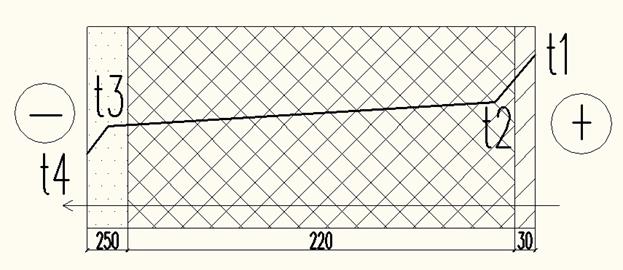
Рисунок 2.3 - Изменение температуры в наружной стене Температурное поле на этом рисунке имеет совершенно загадочные перегибы. С чего бы? Значение термического сопротивления всей конструкции и теплового потока в этом случае останется прежним:
Определяем температуры на границах слоев конструкции по формуле:
где tx - температура в любой точке конструкции, °С; Rx - часть термического сопротивления, находящегося между плоскостями c температурами t1 и tx, (м2 ∙ ºС)/Вт.
Граница промерзания находится в слое «маты минераловатные прошивные». Определяем глубину промерзания в теплоизоляционном слое и составляем пропорцию:
Отсюда х=0,08 м
Общая глубина промерзания в этом случае составит: δпр =0,3+х =0,38 м.
Рисунок 2.4 – Глубина промерзания в теплоизоляционном слое Откорректить рисунок в соответствии со здравым смыслом. И с физическим тоже!
Вывод: Глубина промерзания, в первом случае составляет 90 мм, во втором случае 380 мм. Экономически целесообразнее делать теплоизоляция как представлено в первом случае, при этом точка росы переносится в теплоизоляционный слой и стена незначительно промерзает в отличие от теплоизоляция, которая представлена во втором случае. При наружной теплоизоляции ограждающая конструкция аккумулирует тепло, потери тепла минимальны. Трудно вам, бедным. У всех общий папа чукча…На русский переведи. Или на английский - лишь бы предлоги с падежами согласовывались |



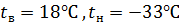
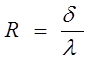 ,
,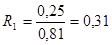 (м2 ∙ ºС)/Вт;
(м2 ∙ ºС)/Вт;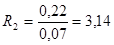 (м2 ∙ ºС)/Вт;
(м2 ∙ ºС)/Вт;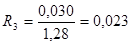 (м2 ∙ ºС)/Вт;
(м2 ∙ ºС)/Вт;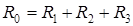 =0,31+3,14+0,023=3,473 (м2 ∙ ºС)/Вт.
=0,31+3,14+0,023=3,473 (м2 ∙ ºС)/Вт.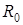 =3,2? По слоям уточнить!
=3,2? По слоям уточнить!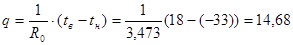 Вт/м2,
Вт/м2,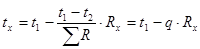 ,
,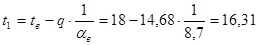 ºС;
ºС;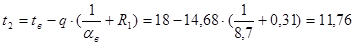 ºС;
ºС; ºС;
ºС;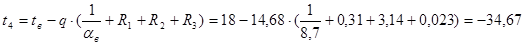 ºС;
ºС;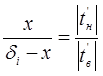
 ;
;

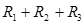 =0,31+3,14+0,023=3,473 (м2 ∙ ºС)/Вт.
=0,31+3,14+0,023=3,473 (м2 ∙ ºС)/Вт.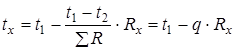 ,
,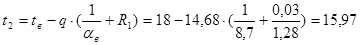 ºС;
ºС;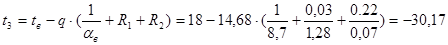 ºС;
ºС; ºС;
ºС;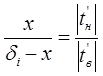
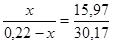 ;
;