ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задание 3. Расчет неритмичных потоков
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный политехнический университет» Инженерно-строительный факультет Кафедра «Технологии, организации и экономики строительства»
Курсовая работа по дисциплине «Организация, планирование и управление строительством». “Организационно-технологические модели строительного производства”
Выполнила студентка гр.5019/2: Стрижкова Я.Н.
Преподаватель: Морозова Т.Ф.
Санкт-Петербург, 2011 г.
Организационно-технологические модели строительного производства Задача курсовой работы Задачей курсовой работы является закрепление студентом знаний полученных при прохождении теоретического курса «Организационно-технологические модели строительного производства». Задание 1. Расчет ритмичного потока
Определить продолжительность (Т) ритмичного потока, если заданы: трудоемкость (Q) каждого вида работ (частного потока), число видов работ (m), число исполнителей (N), занятых в данном частном потоке, и число частных фронтов (n). Представить график Ганта ритмичного потока. Q=45 N=3 m=4 n=4
Решение: Тритм = r×(m+n-1)
Тритм = 5×(4+4-1)=35 (дн.)
График Ганта
Расписание выполнения работ ритмичного потока
Пример 2. Расчет разноритмичных потоков Дано три различных комплекса работ, состоящих из трех видов работ, выполняемых на трех фронтах. Работы внутри каждого вида выполняются ритмично, а между собой ритмы различаются. Требуется рассчитать разноритмичные потоки с непрерывным использованием ресурсов. Представить в виде циклограммы рассчитанных потоков. r1=5 r2=6 r3=7 r1=7 r2=6 r3=5 а) расходящийся поток
Т= TВразв.+TБразв.+ åtiВ =5+6+7·4=39 дней ТБ, ТВ – периоды развертывания потоков Б и В. Равны ритмам предшествующих потоков
Циклограмма расходящегося потока
б) сходящийся поток
Т=åtiA+Тсв.Б+Тсв.В=7·4+6+5=39 дней Тсв.Б, Тсв.В – периоды свертывания потоков Б и В равны ритмам потоков
Циклограмма сходящегося потока
Задание 3. Расчет неритмичных потоков Дан неритмичный поток. Требуется сформировать и рассчитать следующие методы организации работ: 3.1 неритмичный поток с непрерывным использованием ресурсов 3.2 неритмичный поток с непрерывным освоением фронтов работ 3.3 неритмичный поток с критическими работами 3.4 для потока с критическими работами построить и рассчитать сетевой график в форме «работы-вершины» Графа
3.1 Расчет по методу с непрерывным использованием ресурсов (НИР) Расчет осуществляется путем суммирования периодов развертывания последующих и продолжительности последних частных потоков. Период развертывания частного потока Б: применительно к I частному фронту ко II частному фронту к III частному фронту к IV частному фронту
Период развертывания частного потока В:
Период развертывания частного потока Г:
Продолжительность потока Т=10+4+9+13=36 Сформированный таким образом поток представлен на матрице:
3.2 Расчет по методу с непрерывным освоением фронтов работ
Неритмичный поток с непрерывным освоением фронтов работ может быть рассчитан (так же, как и п. 3.1) путем суммирования периодов развертывания фронтальных комплексов и продолжительности работ последнего фронтального комплекса. Для расчета транспонируем матрицу:
Период развертывания частного фронта работ II:
Период развертывания частного фронта работ III:
Период развертывания частного фронта работ IV:
Продолжительность потока Т=13+2+13+15=43
3.3 Расчет по методу с критическими и некритическими работами, выявленными с учетом ресурсных и фронтальных связей
1 шаг: подсчитываются ранние сроки выполнения работ, входящих в первый частный поток и в первый частный комплекс. Поскольку на первый частный поток фронтальные связи не действуют (их нет, т.к. нет предшествующих по виду работ), то в данном случае ранние сроки выполнения работ определяются однозначно по формуле
Для работы ТАI=0+6=6 ТAII=6+2=8 ТAIII=8+9=17 TAIV=17+2=19
2 шаг: подсчитываем ранние сроки выполнения всех прочих работ по мере возможности. Первая возможность появляется у работы БII. ранний срок начала этой работы определится формуле
Действительно, для того, чтобы работа началась, необходимы фронт работ и ресурсы, которые высвобождаются после завершения предшествующих работ. После определения ранних сроков данной работы могут определяться ранние сроки последующих за нею работ, например, В II.
Ранние сроки работ вписываются в верхнюю часть клетки матрицы.
3 шаг: подсчитываются поздние сроки выполнения работ, входящих в последний частный поток (последний столбец) и в комплексе работ на последнем частном фронте (последняя строка)
Для работы ГIV=36-3=33 В IV=33-4=29; Г III=33-1=32 и т.д. Поздние сроки вписываем в нижнюю часть клетки матрицы.
4 шаг: подсчитываются поздние сроки выполнения всех прочих работ по мере возможности. Первая возможность появилась у работы В III. Поздний срок окончания этой работы определится по формуле
Затем могут определяться поздние сроки остальных работ.
5 шаг: определяются полные резервы времени как разница между поздним и ранним началом или окончанием каждой работы.
3.4 Представление расчетной матрицы в виде сетевого графика (вершины-работы) Элементами такого графика являются работы и зависимости. Зависимость показывает организационно-технологическую связь между работами и изображается стрелкой. Данная форма модели удобна для расчета на ПК с помощью Time Line, MS Project, Primavera и т.д.
|



 (дн.)
(дн.)








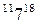






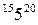
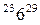
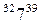









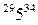




 ;
;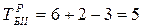 ;
; ;
; ;
;
 ;
; ;
;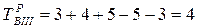 ;
; ;
;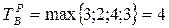 .
. ;
; ;
; ;
; ;
;





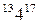







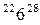


 ;
; ;
;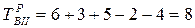 ;
; ;
;
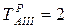 ;
; ;
; ;
; ;
;
 ;
; ;
; ;
; ;
;














 ТБ1=6+3=9 ТВ1=9+5=14 ТГ1=14+8=22
ТБ1=6+3=9 ТВ1=9+5=14 ТГ1=14+8=22





 ;
;  ;
;  ;
;







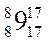







 13
13