 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Нахождение линейной и квадратичной аппроксимирующих функций
Курсовая работа по предмету Информатика Тема: Численные методы и оптимизация Выполнил: Студент 2 курса Специальность 210406 Студ. билет №7СС10014 Цветков А. В. Преподаватель: Саладаев Е. Н. Нижний Новгород Год
Задание 1. Получить линейную - выполнить расчет параметров линейной аппроксимирующей функции; - получить систему нормальных уравнений и выполнить расчет ее параметров для проведения квадратичной аппроксимирующей функции; - проверить полученные результаты; - вычислить значения аппроксимирующих функций в узлах аппроксимации; - построить график заданной функции (множество заданных точек) и графики функций линейной и квадратичной аппроксимации; - оценить качество аппроксимации. 2. Найти два корня уравнения - отделить корни уравнения; - проверить (аналитически) условия сходимости применяемых методов решения уравнений. В случае необходимости привести уравнение к виду, обеспечивающему сходимость процесса приближения к корню; - выбрать начальные приближения; - записать рекуррентную формулу для уточнения корня и произвести по ней расчеты; - оценить погрешности. 3. Вычислить - оценить погрешность. 4. Определить точку экстремума функции - проверить условие унимодальности функции и выбрать начальный отрезок оптимизации; - провести расчеты по сокращению отрезка оптимизации и проверить условие окончания поиска минимума (максимума) функции.
Нахождение линейной и квадратичной аппроксимирующих функций
Исходная функция
Линейная аппроксимирующая функция имеет вид Найдем параметры линейной аппроксимации:
Проверим полученные данные средствами MathCad:
или
Искомая линейная аппроксимирующая функция примет вид:
Квадратичная аппроксимирующая функция имеет вид
Запишем в следующую таблицу элементы матрицы Грама и столбец свободных членов:
Система нормальных уравнений примет вид:
Найдем решение этой системы уравнений:
Проверим полученные данные средствами MathCad:
Искомая квадратичная аппроксимирующая функция примет вид:
Значения исходной функции y(x), а также аппроксимирующих функций Flin(x) и Fsq(x) в узлах аппроксимации приведены в таблице 3:
Графики функций линейной и квадратичной аппроксимации показаны на рисунке
Оценим качество аппроксимации:
Для линейной функции: ρlin=0.654 Для квадратичной функции: ρsq=0.547 Получили, что ρ2<ρ1, из чего можно сделать вывод, что квадратичная аппроксимация более качественная.
2. Решение уравнения Fsq(x)=0 с точностью E = 10-3.
Решим уравнение Найдем производные функции Fsq(x):
Для отделения корней уравнения составим таблицу знаков функции Fsq(x) и ее производной Fsq’(x):
На отрезках [7;9] и [17;19] функция Fsq(x) меняет знак, т.е. существует, по крайней мере, по одному корню, принадлежащему каждому из этих отрезков. Поскольку знак первой (и второй) производной на выбранных отрезках остается постоянным, то можно сказать, что функция на этих отрезках монотонна. Следовательно, выбранные отрезки содержат по одному корню.
1) Уточним первый корень уравнения Fsq(x)=0 на отрезке [7;9] методом Ньютона. Проверим выполнение достаточных условий сходимости метода Ньютона: Fsq(x) непрерывна на отрезке [7;9] Fsq(7)∙Fsq(9)<0 Fsq’(x) и Fsq”(x) отличны от нуля и сохраняют знаки при Выберем начальное приближение x0, удовлетворяющее условию Возьмем x0=8, поскольку Fsq”(x)=-0.076<0 и Fsq(8)<0. Рекуррентная формула для уточнения корня уравнения по методу Ньютона:
Уточним корень уравнения на отрезке [7;9]. Условие окончания поиска корня: Результат запишем в таблицу:
Оценим погрешность вычисления 1-го корня после 3 итераций, используя формулу Получим Проверим найденный корень уравнения средствами MathCad:
Таким образом, x1=7.4864.
2) Уточним второй корень уравнения Fsq(x)=0 на отрезке [17;19] методом итераций. Fsq(x) дифференцируема и имеет разные знаки на отрезке [17;19]. Найдем итерирующую функцию. Итерирующая функция
В нашем случае r=0.47 и Fsq’(x)>0, следовательно, Запишем рекуррентную формулу для вычисления приближений к корню:
Выберем начальное приближение к корню, например, x0=2. Условие окончания поиска корня: Результат запишем в таблицу:
Оценим погрешность вычисления 2-го корня после 4 итераций, используя формулу
Получим
Таким образом, x2=18.14518.
3. Вычисление определенного интеграла
Вычислим интеграл
Метод средних прямоугольников:
Метод трапеций:
Метод Симпсона:
Результаты занесем в таблицу:
Оценка погрешности по правилу Рунге:
Для методов средних прямоугольников и трапеций при k=2 Rср.пр. = 0.065 Rтрап. = 0.077 Для метода Симпсона при k=4 RСимп. = 5.167∙10-3
Вычислим значение
4. Определение точки экстремума функции Fsq(x) методами одномерной оптимизации с точностью E=10-2.
Для нахождения точки экстремума функции Выясним, унимодальна ли функция Fsq(x), и выберем отрезок неопределенности. Рассмотрим отрезок [12.5;13.5].
Получили, что функция Fsq(x) дважды дифференцируема на рассматриваемом отрезке, ее первая производная Fsq’(x) не убывает на этом отрезке, а вторая производная Fsq’’(x)>0. Таким образом, на отрезке [12.5;13.5] функция Fsq(x) унимодальна, и, следовательно, этот отрезок может быть выбран в качестве начального отрезка неопределенности. Найдем точку экстремума методами дихотомии и золотого сечения. Условия прекращения поиска:
Метод дихотомии:
После 8 итераций получили xmin=13.25873 и Fsq(xmin)=14.43217.
Метод золотого сечения:
После 10 итераций получили xmin=13.25985 и Fsq(xmin)=14.43439.
Выполним задачу оптимизации средствами MathCad:
Список литературы: 1. Конспект лекций по информатике 2. Методические указания и контрольные задания по дисциплине Информатика. Численные методы и оптимизация. Г.К.Сосновиков, И.Б.Юскова, Н.П.Муравьев. 2008 г. 3. Практическое решение инженерных и научных задач на ПК с использованием математических пакетов. В.Н.Шакин, Т.И.Семенова, О.М.Кравченко. 2010 г. |
и квадратичную 
аппроксимирующие функции заданной функции y(x) методом наименьших квадратов для степенного базиса:
с заданной точностью 
:
при разбиении отрезка интегрирования на n1=10 и n2=20 интервалов, где x1, x2 - корни уравнения 
методами одномерной оптимизации (с точностью 
):
задана таблицей.
.
.
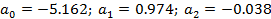
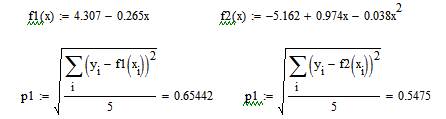
, где 
, 
.
.
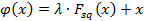обеспечивает выполнение условия сходимости 
для 
. Выберем параметр λ по правилу:
. Пусть λ=-2.
, где 
.
проверим найденный корень уравнения средствами MathCad:
методами Симпсона, трапеций и средних прямоугольников, полагая n1=10 и n2=20.
применим методы дихотомии и золотого сечения.
