 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ЗАДАЧИ К КОНТРОЛЬНЫМ ЗАДАНИЯМ 12
СТАТИКА В статике рассматривается а) теория сил, б) равновесие тел под действием различных систем сил. Все задачи контрольного задания (С1-C3) относятся к теме о равновесии. Это позволяет привести общие для всех задач сведения справочного характера из теории и сформулировать алгоритм решения задач.
ВИДЫ СВЯЗЕЙ Связь – тело, препятствующее перемещению данного объекта (тела, узла) в пространстве. Реакция связи – сила, с которой связь действует на объект.
ОСНОВНЫЕ ПОНЯТИЯ
ВИДЫ СИСТЕМ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, И УРАВНЕНИЯ РАВНОВЕСИЯ
Примерный план (алгоритм) решения задач статики: 1. Назвать (выделить) объект: тело, узел, равновесие которого надо рассмотреть в данной задаче. 2. Указать на рисунке силы, действующие на этот объект: а) активные силы; б) назвать каждую связь и пояснить направление реакций связи или их составляющих (мысленно освобождая объект от связи на основании аксиомы освобождения от связей); 3. Назвать вид полученной системы сил, учитывая расположение линий действия сил. 4. Сформулировать условия равновесия полученной системы сил в алгебраической (координатной) форме. 5. Провести на рисунке координатные оси (если заранее не потребовалось это сделать). 6. Составить уравнения равновесия. 7. Решить систему уравнений с пояснением. 8. Сделать проверку. 9. Записать ответ.
При работе необходимо использовать учебник, данное пособие и справочник по математике. Задача С1
Жесткая рама, расположенная в вертикальной плоскости (рис. С1.0-С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках. В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25 кН. На раму действуют пара сил с моментом М = 100 кН×м и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях № 1 на раму действуют сила Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять a = 0,5 м. Указания. Задача C1 – на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента какой-либо силы
Таблица С1
Перед выполнением задания прочтите по учебнику темы: «Основные понятия и аксиомы статики», «Связи и реакции связей», «Плоская система сил», «Пара сил». Вопросы, на которые следует обратить внимание и выучить: 1. Сила, линия действия силы. 2. Проекция силы на ось. В каком случае проекция силы на ось равна нулю? 3. Проекция силы на плоскость, в каком случае эта проекция равна нулю. Отличие проекции силы на плоскость от проекции силы на ось. 4. Алгебраической момент силы относительно центра (точки). В каком случае момент силы относительно центра равен нулю? 5. Что называется связями, перечислите виды связей. 6. Аксиома освобождения от связей. 7. Реакция связи, ее направление и точка приложения. 8. Какая система сил называется плоской (произвольной плоской)? Сформулировать и записать уравнения: условия равновесия плоской системы сил в векторной и алгебраической (координатной) формах.
Пример C1. Жесткая пластина ABCD (рис. C1) имеет в точке А неподвижную шарнирную опору, а в точке В - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.
Решение. Рассмотрим равновесие пластины. Проведем координатные оси ху и изобразим действующие на пластину силы (рис. C1): а) активные силы (нагрузки): силу б) реакции связей: в точке A связью является неподвижная шарнирная опора, ее реакцию изображаем двумя составляющими в точке В связью является подвижная шарнирная опора на катках, ее реакция направлена перпендикулярно плоскости опоры катков; в точке D связью является трос, реакция троса Получилась плоская система сил; составим три уравнения равновесия. При вычислении момента силы
Решение системы уравнений начинаем с уравнения (3), так как оно содержит одну неизвестную
Подставляем
Подставляем
Проверка.Составим, например, уравнение
Ответ:ХА = -8,5 кН, YA = -23,3 кН, RB = 7,3 кН. Знаки указывают, что составляющие реакции шарнира В примерах выполнения последующих задач решение уравнений и проверка не приводятся, но это необходимо делать при выполнении каждой задачи контрольной работы. Задача С2 Шесть невесомых стержней соединены своими концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам А, В, С, D (рис. С2.0-С2.9, табл. С2). Стержни и узлы (узлы расположены в вершинах H, К, L или M прямоугольного параллелепипеда) на рисунках не показаны и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила P=200 Н; во втором узле приложена сила Q=100 Н. Сила Грани параллелепипеда, параллельные плоскости ху, – квадраты. Диагонали других боковых граней образуют с плоскостью ху угол На рис. С2.10 в качестве примера показано, как должен выглядеть чертеж С2.1, если по условиям задачи узлы находятся в точках L и М, а стержнями являются LM, LA, LB; МА, МС, MD. Там же показаны углы Указания. Задача С2 – на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть закон о равенстве действия и противодействия; начинать с узла, где сходятся три стержня. Изображать чертеж можно без соблюдения масштаба так, чтобы лучше были видны все шесть стержней. Стержни следует пронумеровать в том порядке, в каком они указаны в таблице; реакции стержней обозначать буквой с индексом, соответствующим номеру стержня (например,
Таблица С2
12 |





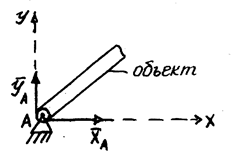
 направлена по нормали к поверхности объекта.
направлена по нормали к поверхности объекта.
 ,
,  .
.


 ,
,  . Направление реакции подпятника A в пространстве не определено; указываем в пространстве три составляющие этой реакции по коорд. осям:
. Направление реакции подпятника A в пространстве не определено; указываем в пространстве три составляющие этой реакции по коорд. осям:  .
.
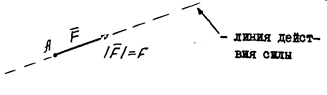





 алгебраическое значение этого момента:
алгебраическое значение этого момента:  . Знак
. Знак  соответствует повороту тела вокруг центра А против хода часовой стрелки; h – перпендикуляр, опущенный из центра А на линию действия силы (плечо силы)
соответствует повороту тела вокруг центра А против хода часовой стрелки; h – перпендикуляр, опущенный из центра А на линию действия силы (плечо силы)
 ,
, 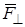 – проекция силы на плоскость, перпендикулярную оси; А – точка пересечения оси с этой же плоскостью; h – плечо силы
– проекция силы на плоскость, перпендикулярную оси; А – точка пересечения оси с этой же плоскостью; h – плечо силы  .
. 
 – две равные антипараллельные силы:
– две равные антипараллельные силы: 


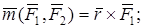 Момент пары сил, действующей на твердое тело, – свободный вектор. Алгебраическое значение момента пары сил:
Момент пары сил, действующей на твердое тело, – свободный вектор. Алгебраическое значение момента пары сил: 
 – плечо пары сил (перпендикуляр, опущенный из точки приложения силы на линию действия другой силы)
– плечо пары сил (перпендикуляр, опущенный из точки приложения силы на линию действия другой силы) (для равновесия произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы сил равнялись нулю). Координатная форма (аналитическая):
(для равновесия произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы сил равнялись нулю). Координатная форма (аналитическая): 2.
2.  3.
3. 
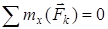 5.
5.  6.
6. 
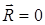 , где
, где  – равнодействующая системы сил. Координатная форма: 1.
– равнодействующая системы сил. Координатная форма: 1.  параллельна линиям действия сил): 1.
параллельна линиям действия сил): 1.  ; 2.
; 2.  . 2-я форма (точки A, B, С не лежат на одной прямой): 1.
. 2-я форма (точки A, B, С не лежат на одной прямой): 1.  ; 3.
; 3.  3-я форма (Ось ОХ не перпендикулярна прямой АВ): 1.
3-я форма (Ось ОХ не перпендикулярна прямой АВ): 1. 










 Плоская система параллельных сил – линии действия сил параллельны и расположены в одной плоскости.
Плоская система параллельных сил – линии действия сил параллельны и расположены в одной плоскости.  под углом 15° к горизонтальной оси, приложенная в точке D, и сила
под углом 15° к горизонтальной оси, приложенная в точке D, и сила  под углом 60° к горизонтальной оси, приложенная в точке E, и т. д.)
под углом 60° к горизонтальной оси, приложенная в точке E, и т. д.) часто удобно разложить ее на составляющие
часто удобно разложить ее на составляющие  и
и  (по правилу параллелограмма), для которых плечи легко определяются; затем применить теорему Вариньона (в алгебраической форме):
(по правилу параллелограмма), для которых плечи легко определяются; затем применить теорему Вариньона (в алгебраической форме):  .
.



 , град.
, град. , град.
, град. , град.
, град. , град.
, град. Рис. С1.0
Рис. С1.0 Рис. С1.1
Рис. С1.1 Рис. С1.2
Рис. С1.2 Рис. С1.3
Рис. С1.3 Рис. С1.4
Рис. С1.4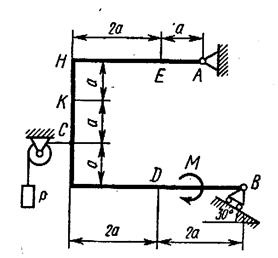 Рис. С1.5
Рис. С1.5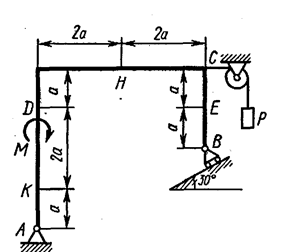 Рис. С1.6
Рис. С1.6 Рис. C1.7
Рис. C1.7 Рис. C1.8
Рис. C1.8 Рис. C1.9
Рис. C1.9
 , l= 0,5 м. Определить: реакции в точках А и В, вызываемые действующими нагрузками.
, l= 0,5 м. Определить: реакции в точках А и В, вызываемые действующими нагрузками. и пару сил с моментом М;
и пару сил с моментом М; , параллельными координатным осям;
, параллельными координатным осям; направлена вдоль троса от пластины (по модулю Т = Р).
направлена вдоль троса от пластины (по модулю Т = Р). и воспользуемся теоремой Вариньона в алгебраической форме:
и воспользуемся теоремой Вариньона в алгебраической форме:  . Получим
. Получим (1)
(1)
 (2)
(2) (3)
(3) :
:
 кН.
кН. .
.
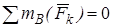 (или уравнение моментов относительно любой другой точки (кроме А). Если задача решена верно, то эта сумма моментов должна получиться равной нулю.
(или уравнение моментов относительно любой другой точки (кроме А). Если задача решена верно, то эта сумма моментов должна получиться равной нулю.

 и
и 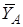 направлены противоположно показанным на рис. C1.
направлены противоположно показанным на рис. C1. образует с положительными направлениями координатных осей х, y, z углы, равные соответственно
образует с положительными направлениями координатных осей х, y, z углы, равные соответственно  ,
,  ,
,  , а сила
, а сила  – углы
– углы  ,
,  ,
,  ; направления осей х, у, z для всех рисунков показаны на рис. С2.0.
; направления осей х, у, z для всех рисунков показаны на рис. С2.0. , а диагональ параллелепипеда образует с этой плоскостью угол
, а диагональ параллелепипеда образует с этой плоскостью угол  . Определить усилия в стержнях.
. Определить усилия в стержнях.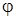 и
и  ; при решении своей задачи на рисунке следует указать заданные значения этих углов.
; при решении своей задачи на рисунке следует указать заданные значения этих углов. ,
, 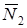 и т.д.).
и т.д.). Рис. С2.0
Рис. С2.0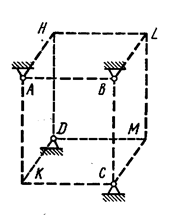 Рис. C2.1
Рис. C2.1 Рис. C2.2
Рис. C2.2 Рис. С2.3
Рис. С2.3 Рис. С2.4
Рис. С2.4 Рис. С2.5
Рис. С2.5 Рис. С2.6
Рис. С2.6 Рис. С2.7
Рис. С2.7 Рис. С2.8
Рис. С2.8 Рис. С2.9
Рис. С2.9 Рис. С2.10
Рис. С2.10