 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Двухвыборочный t-критерий для независимых выборок 12
Алгоритмы параметрических критериев. Параметрические критерии применяются для выборок с нормальным законом распределения. Формула расчета этих критериев содержат параметры выборки: среднее, дисперсии и др. Поэтому они называются параметрическими. Нормальность закона распределения должна быть статистически доказана с помощью одного из критериев согласия: критерий Пирсона, F-критерия Фишера, В ряде случаев параметрические критерии мощнее непараметрических критериев. У последних выше вероятность возникновения ошибки второго рода – принятия ложной нулевой гипотезы. К параметрическим методам относятся следующие: – Критерий Стьюдента – Критерий Фишера – Методы однофакторного анализа – Методы двухфакторного анализа
Критерий Стьюдента Назначение. Критерий позволяет оценивать различия средних значений выборок, имеющих нормальное распределение. Описание критерия. Критерий применим для сравнения средних значений двух выборок полученных до и после воздействия некоторого фактора.
Двухвыборочный t-критерий для независимых выборок Для двух несвязанных выборок(наблюдения не относятся к одной и той же группе объектов ) возможны два варианта расчета: – когда дисперсии известны – когда дисперсии неизвестны, но равны друг другу. 1. Предварительно проверяется нормальность закона распределения по одному из критериев согласия. 2. Рассчитывается средне арифметические значения 3. Рассчитывается
Где квадратичного отклонения. Здесь
Рассмотрим сначала равночисленные выборки . В этом случае
В случае наравночисленных выборок
В обоих случаев подсчет числа степеней свободы осуществляется по формулам
Понятно, что при численном равенстве выборок 4. Эмпирическое значение Нулевая гипотеза Пример. Психолог измерял время сложной сенсомоторной реакции выбора (в мс) в контрольной и экспериментальных группах. В экспериментальную группу (Х) входило 9 спортсменов высокой квалификации. Контрольной группой (Y) являлись 8 человек, активно не занимающиеся спортом. Психолог проверяет гипотезу о том , что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем та же величина у людей, не занимающихся спортом.
Cреднее арифметические значения X и У:
Тогда
Число степеней свободы k=9+8-2=15 12 |



 -критерия Колмогорова и др.
-критерия Колмогорова и др. и
и  для каждой выборки по формуле
для каждой выборки по формуле  где
где  – значение i-го результата наблюдения.
– значение i-го результата наблюдения. - эмпирическое значение критерия Стьюдента:
- эмпирическое значение критерия Стьюдента:

 и
и  – оценки дисперсий.
– оценки дисперсий.

 , выражение
, выражение

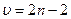
 критерия Стьюдента сравнивается с критическим значением
критерия Стьюдента сравнивается с критическим значением  (по таблице 1 приложения) для данного числа степеней свободы.
(по таблице 1 приложения) для данного числа степеней свободы. при заданном уровне значимости
при заданном уровне значимости  принимается, если эмпирическое значение
принимается, если эмпирическое значение  .
.



 , в контрольной группе
, в контрольной группе  .
.

