ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задачи к контрольному заданию
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ИЖЕВСКАЯ ГОСУДАТРСВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Методические указания и контрольные задания
Для студентов-заочников инженерных специальностей
Составитель: ст. преподаватель каф. ТМСМ Н.В.Гусева
Содержание заданий, выбор вариантов, порядок выполнения работ, пояснения к тексту задач
Студенты выполняют контрольное задание, включающее 5 задач. Задача С1 – равновесие под действием произвольной плоской системы сил. Задача С2 – равновесие составной конструкции. Задача К1 – кинематика поступательного и вращательного движения. Задача К2 – кинематика плоского механизма. Задача К3 – кинематика сложного движения точки. К каждой задаче дается 10 рисунков и таблица (с тем же номером, что и задача), содержащая дополнительные к тексту задачи условие. Нумерация рисунков двойная, при этом номером рисунка является последняя цифра. Студент во всех задачах выбирает номер рисунка по предпоследней цифре шифра, а номер условия в таблице – по последней. Контрольное задание выполняется в отдельной тетради. На обложке указываются: название дисциплины, номер работы, фамилия и инициалы студента, учебный шифр, факультет и специальность. Чертеж к задаче выполняется с учетом условий решаемого варианта задачи; на нем все углы, действующие силы, число тел и их расположение на чертеже должны соответствовать этим условиям. Чертеж должен быть ясным и наглядным, а его размеры должны позволять ясно показывать все силы или векторы скорости, ускорения и др. Не забудьте на чертеже указать расположение координатных осей. При выполнении задания все преобразования и числовые расчеты должны быть последовательно проделаны с необходимыми пояснениями, в конце должны быть даны ответы. Числовые данные подставлять в полученную расчетную формулу. Студент с выполненной контрольной работой приходит на экзамен. Экзаменационная работа выполняется в этой же тетради и в конце экзамена сдается на проверку.
Задачи к контрольному заданию
Статика Задача С1
Жесткая рама массой 1000 кг закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом 25 кН. На раму действует пара сил с моментом М = 60 кН м и две силы, значения которых указаны в таблице. Определить реакции связей в точках А, В, вызываемые действующими нагрузками. При окончательных расчетах принять а = 0,5 м. Указания. Задача С1 – на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжение обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковы. Силу тяжести рамы приложить к ее центру тяжести, положение центра тяжести определить. Чтобы уравнение моментов было более простым, нужно брать моменты относительно точки, в которой пересекаются линии действия двух реакций связей. При вычислении моментов силы, не параллельные выбранным координатным осям, удобно разложить на составляющие
Задача С2
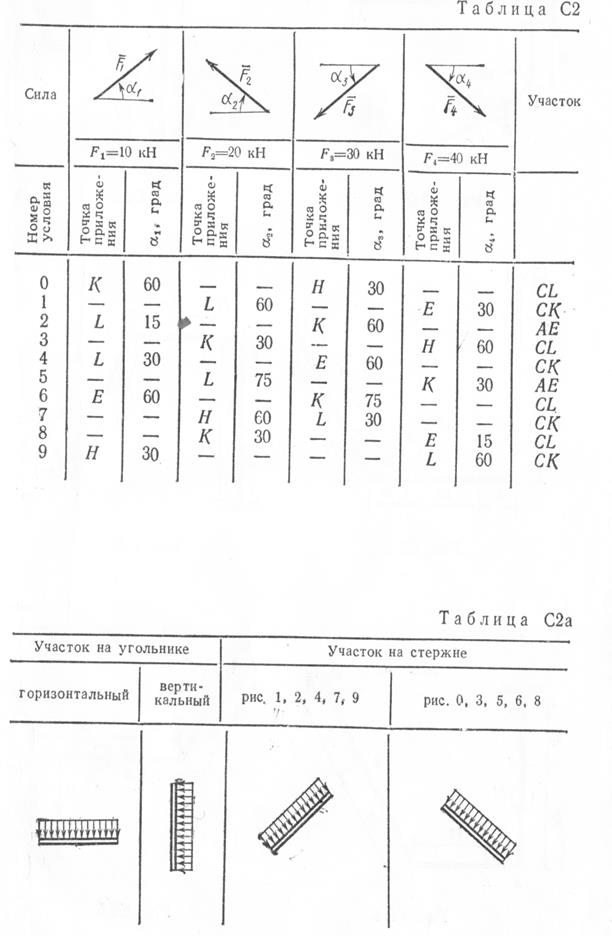
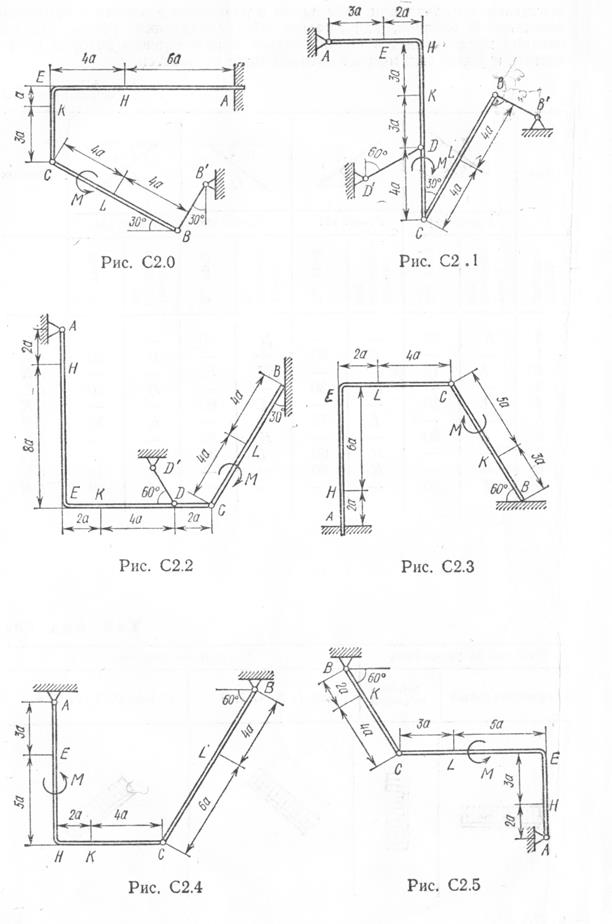
Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно или свободно опираются друг о друга. На конструкцию действует пара сил с моментом М = 60 кН м, распределенная нагрузка интенсивности q = 20 кН/м и две силы, значения которых , точки приложения и направления имеются в таблице; в этой же таблице в столбце «Участок» указано, на каком участке действует распределенная нагрузка. Определить реакции связей в точках А,В,С ( для рис. 1,2,7,9 еще и в точке D ), вызванные данными нагрузками. При окончательных расчетах принять а = 0,2 м. Указания. Задача С2 – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении следует расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия.
Задача К1
Механизм состоит из ступенчатых колес 1 -3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 - В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где Определить в момент времени Указания. Задача К1 – на исследование простейших движений твердого тела. При решении задачи учесть, что при зацеплении колес скорости точек зацепления одинаковы, а при ременной передаче скорости всех точек ремня и, следовательно, точек, лежащих на ободе этих колес одинаковы при отсутствии проскальзывания и растяжения ремня. Таблица К1
Рис. К1.0 Рис. К1.1
Рис. К1.2 Рис. К1.3
Рис. К1.4 Рис. К1.5
Рис. К1.6 Рис. К1.7
Рис. К1.8 Рис. К1.9
Пример К1. Рейка 1, ступенчатое колесо 2 с радиусами
Задача К2
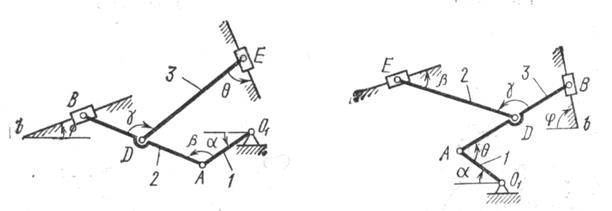
Плоский механизм состоит из стержней 1,2,3,4, и ползуна В или Е. Точка D находится в середине стержня АВ. Длины стержней соответственно равны: Определить величины, указанные в таблицах в столбцах «Найти». Причем скорости указанных точек определить двумя способами: графоаналитическим, как показано в примере, и аналитическим. Построение чертежа начинать со стержня, направление которого определяется углом Заданные угловую скорость и угловое ускорение считать направленными против хода часовой стрелки, а заданные скорости Указания. Задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении воспользоваться теоремами о скоростях и ускорениях точек плоской фигуры, а также понятием о мгновенном центре скоростей.
Таблица К2а (к рис. К2.0-К2.4)
Таблица К2б (к рис. К2.5-К2.9)
Рис. К2.0 Рис.К2.1
Рис.К2.2 Рис.К2.3
Рис.К2.4 Рис.К2.5
Рис.К2.6 Рис.К2.7
Рис.К2.8 Рис.К2.9 Пример К2. Механизм (рис.К2.а) состоит из стержней 1,2,3,4 и ползуна В, соединенных друг с другом и с неподвижными опорами
Задача К3
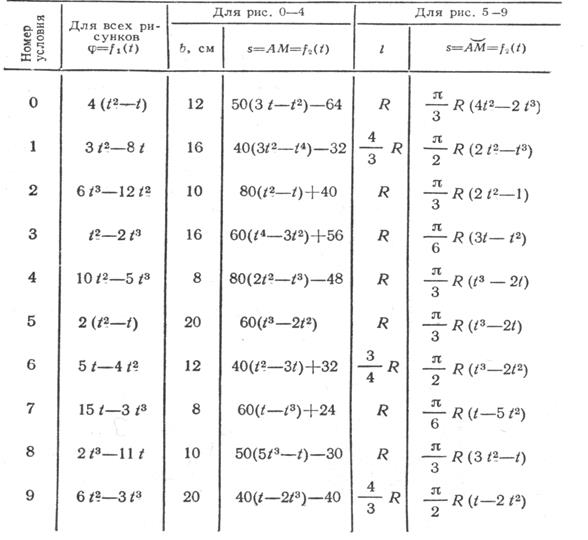
Прямоугольная пластина (рис.К3.0-К3.4) или круглая пластина радиуса R=60 см (рис.К3.5-К3.9) вращается вокруг неподвижной оси по закону По пластине вдоль прямой ВD (рис. 0-4) или по окружности радиуса R (рис. 5-9) движется точка М; закон ее относительного движения, т.е. зависимость Найти абсолютную скорость и абсолютное ускорение точки М в момент времени Указания. Задача К3 – на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и сложении ускорений при сложном движении точки. Прежде чем проводить расчеты, следует по условию задачи определить, где находится точка М на пластине в момент времени В случаях, относящихся к рис. 5-9, при решении задачи не подставлять числового значения R, пока не будут определены положения точки М в момент времени
Таблица К3
Рис. К3.0 Рис.К3.1 Рис. К3.2
Рис. К3.3 Рис.К3.4 Рис. К3.5
Рис.К3.6 Рис.К3.7
Рис.К3.8 Рис.К3.9
Пример К3 Шар радиуса R (рис К3.а) вращается вокруг своего диаметра АВ по закону
Рис. К3
|




 , для которых плечи легко определяются.
, для которых плечи легко определяются.





 , у колеса 2 -
, у колеса 2 -  , у колеса 3 -
, у колеса 3 -  На ободьях колес расположены точки А,В,С.
На ободьях колес расположены точки А,В,С. - закон вращения колеса 1,
- закон вращения колеса 1,  - закон движения рейки 4,
- закон движения рейки 4,  - закон изменения угловой скорости колеса 2,
- закон изменения угловой скорости колеса 2,  - закон изменения скорости груза 5 и т.д. (везде
- закон изменения скорости груза 5 и т.д. (везде  выражено в радианах,
выражено в радианах,  - в сантиметрах,
- в сантиметрах,  - в секундах). Положительное направление для
- в секундах). Положительное направление для  - против часовой стрелки, для
- против часовой стрелки, для  - вниз.
- вниз. = 1 с указанные в таблице в столбцах «Найти» скорости и ускорения соответствующих точек или тел. Вектора скоростей и ускорений указанных точек или тел изобразить на чертеже, также указать на чертеже круговые стрелки, соответствующие векторам угловых скоростей и угловых ускорений тел, которым принадлежат указанные точки.
= 1 с указанные в таблице в столбцах «Найти» скорости и ускорения соответствующих точек или тел. Вектора скоростей и ускорений указанных точек или тел изобразить на чертеже, также указать на чертеже круговые стрелки, соответствующие векторам угловых скоростей и угловых ускорений тел, которым принадлежат указанные точки.



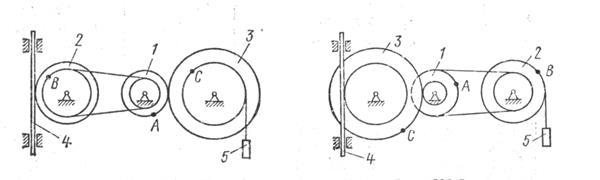

 и колесо 3 радиуса
и колесо 3 радиуса  , скрепленное с валом радиуса
, скрепленное с валом радиуса  находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К.2). Рейка движется по закону
находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К.2). Рейка движется по закону  .
.
 . Положение механизма определяется углами
. Положение механизма определяется углами  . Значения этих углов и других заданных величин указаны в таблице К2а или в таблице К2б, при этом в указанных таблицах
. Значения этих углов и других заданных величин указаны в таблице К2а или в таблице К2б, при этом в указанных таблицах 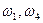 - величины постоянные.
- величины постоянные. ; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б).
; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б). и ускорение
и ускорение  от точки В к b.
от точки В к b.





 шарнирами.
шарнирами.


 , заданному в таблице К3. Положительное направление отчета углов
, заданному в таблице К3. Положительное направление отчета углов  лежит в плоскости пластины (пластина вращается в пространстве).
лежит в плоскости пластины (пластина вращается в пространстве). (
(  . На рисунках точка М показана в положении, при котором
. На рисунках точка М показана в положении, при котором  (при
(при  точка М находится по другую сторону от точки А).
точка М находится по другую сторону от точки А). с.
с. , и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче)
, и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче)