 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задачи к контрольным заданиям 12
Динамика Задача Д1 Груз
Рис. Д1.0 Рис. Д1.1
Рис. Д1.2 Рис. Д1.3
Рис. Д1.4 Рис. Д1.5
Рис. Д1.6 Рис. Д1.7
Рис. Д1.8 Рис. Д1.9 Таблица Д1
На участке Считая груз материальной точкой и зная расстояние Указания. Задача Д1 – на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке
На вертикальном участке
 кг, кг,  , где , где  кг/м, кг/м,  м/с, м/с,  м, м,   . . Определить: Решение: 1. Рассмотрим движение груза на участке
Далее находим
Введем для сокращения записей обозначения:
где при подсчете принято
Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим
По начальным условиям при
В результате находим:
Полагая в равенстве (6)
2. Рассмотрим теперь движение груза на участке
или
где
Разделив обе части равенства на
Умножая обе части уравнения (10) на
Будем теперь отсчитывать время от момента, когда груз находится в точке
При найденном значении
Умножая здесь обе части на
Так как при
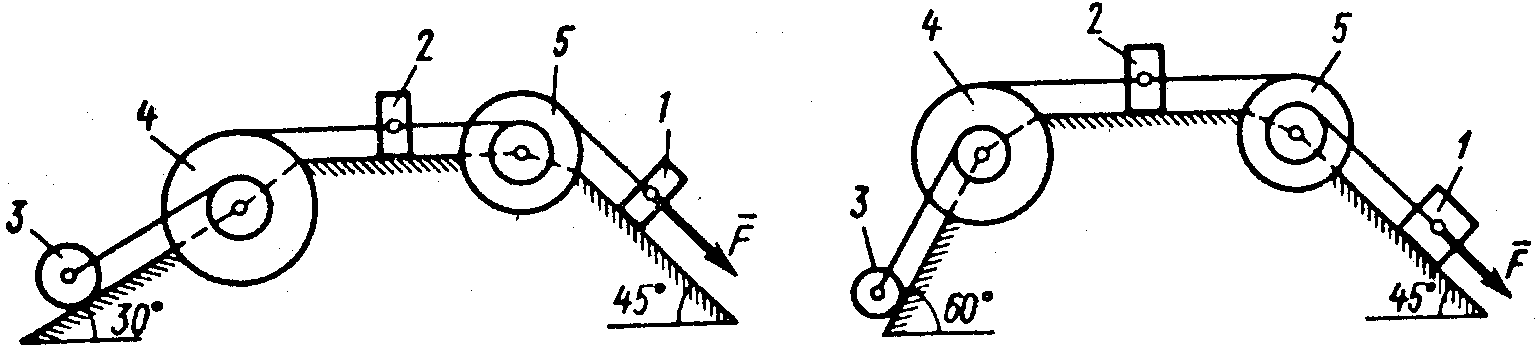
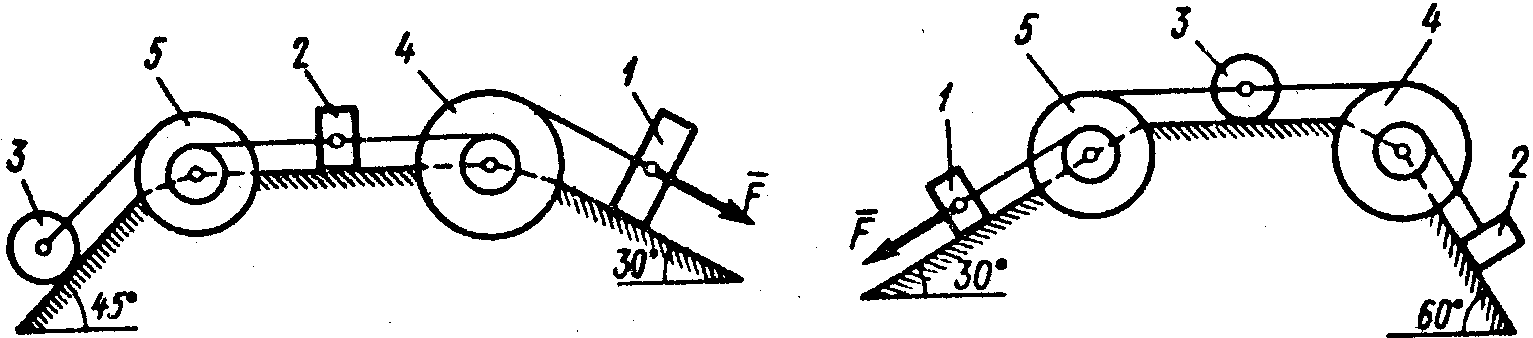
где Ответ: Задача Д2 Механическая система состоит из грузов 1 и 2, цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней
Рис. Д2.0 Рис. Д2.1
Рис. Д2.2 Рис. Д2.3
Рис. Д2.4 Рис. Д2.5
Рис. Д2.6 Рис. Д2.7
Рис. Д2.8 Рис. Д2.9 Таблица Д2
Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Под действием силы Определить значение искомой величины в тот момент времени, когда перемещение
Каток катится по плоскости без скольжения. На всех рисунках можно не изображать груз 2, если Указания. Задача Д2 – на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия Пример Д2.
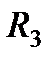 и и  и радиусом инерции относительно оси вращения и радиусом инерции относительно оси вращения  , блока 4 и груза 5 (коэффициент трения груза о плоскость равен , блока 4 и груза 5 (коэффициент трения груза о плоскость равен  ). Тела системы соединены нитями, намотанными на шкив 3. К центру ). Тела системы соединены нитями, намотанными на шкив 3. К центру  блока 2 прикреплена пружина с коэффициентом жесткости блока 2 прикреплена пружина с коэффициентом жесткости  ; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы ; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы  , зависящей от перемещения , зависящей от перемещения  точки ее приложения. На шкив 3 при движении действует постоянный момент точки ее приложения. На шкив 3 при движении действует постоянный момент  сил сопротивления. сил сопротивления. Дано: Определить: Решение: 1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные Для определения
2. Определяем
Учитывая, что тело 1 движется плоскопараллельно, тело 5 – поступательно, а тело 3 вращается вокруг неподвижной оси, получим
Все входящие сюда скорости надо выразить через искомую
Кроме того, входящие в (3) моменты инерции имеют значения
Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно
3. Найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка 1 пройдет путь
Работы остальных сил равны нулю, т.к. точки
 , а так как точка , а так как точка  является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку нити является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку нити  ), то ), то  ; следовательно, и ; следовательно, и  . При найденных значениях . При найденных значениях  и и  для суммы вычисленных работ получим для суммы вычисленных работ получим
Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что
Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость Ответ: Задача Д3 Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3–6, прикрепленных к этим нитям, и невесомого блока (рис. Д3.0–Д3.9, табл. Д3).
Рис. Д3.0 Рис. Д3.1
Рис. Д3.2 Рис. Д3.3
Рис. Д3.4 Рис. Д3.5
Рис. Д3.6 Рис. Д3.7
Рис. Д3.8 Рис. Д3.9
Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом Пренебрегая трением, найти ускорение тела, имеющего больший вес; веса
Таблица Д3
Указания. Задача Д3 – на применение к изучению движения системы уравнений Лагранжа. В задаче система имеет одну степень свободы, ее положение определяется одной обобщенной координатой и для нее должно быть составлено одно уравнение движения. В задачах, где требуется найти ускорение груза 3 (4, 5 или 6), за обобщенную координату удобно принять координату Пример Д3. Механическая система (рис. Д3) состоит из обмотанных нитями блока 1 радиуса
Рис. Д.3
Дано: Определить: ускорение груза 3, пренебрегая трением. Решение: 1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, – идеальные. Выберем в качестве обобщенной координаты перемещение
2. Определим кинетическую энергию всей системы, равную сумме кинетических энергий всех тел:
Грузы 3 и 4 движутся поступательно, поэтому шкив 2 вращается вокруг неподвижной оси, следовательно
Скорости
Подставляя значения величин (4) в равенства (3), а затем значения
Так как кинетическая энергия зависит только от
3. Найдем обобщенную силу
Выразим
В результате получим
Коэффициент при
Подставляя (6) и (8) в уравнение (1), получим
Отсюда находим
Ответ:
КОНТРОЛЬНЫЕ ВОПРОСЫ Задача Д1 1) Основной закон динамики и получение дифференциальных уравнений движения точки. 2) Какие способы интегрирования дифференциальных уравнений используются в случае, когда сила зависит от скорости и когда сила зависит от времени? Задача Д2 1) Как формулируется теорема об изменении кинетической энергии? Использование этой теоремы для изучения движения механических систем с одной степенью свободы. 2) Способы вычисления кинетической энергии твердого тела в случаях поступательного, вращательного и плоскопараллельного движения. 3) Работа силы как характеристика действия силы на перемещении точки приложения силы. Как вычисляется работа постоянной силы, силы, зависящей от смещения, силы упругости? Задача Д3 1) Что такое возможное перемещение точки и системы? 2) Обобщенные координаты, обобщенные скорости и обобщенные силы механической системы. 3) Как записываются уравнения Лагранжа в случае системы, число степеней которой равно 4) Уравнение Лагранжа как алгоритм получения уравнений движения механической системы. Как с помощью этих уравнений могут быть получены дифференциальные уравнения относительно обобщенных координат?
Библиографический список 1. Никитин Н.Н. Курс теоретической механики: учебник для машиностроит. и приборостроит. спец. вузов / Н.Н. Никитин. – М.: Высш. шк., 1990. 607 с. 2. Бутенин Н.В. Курс теоретической механики: в 2х т. / Н.В. Бутенин, Я.Л. Лунц, Д.Р. Меркин. – СПб.: Лань, 2002. 736 с. 3. Тарг С.М. Краткий курс теоретической механики / С.М. Тарг. – М: Высш. шк., 2008. 416 с. 4. Цывильский В.Л. Теоретическая механика / В.Л. Цывильский. – М: Высш. шк., 2008. 368 с. 5. Переславцева Н.С. Теоретическая механика: учеб. пособие / Н.С. Переславцева, Н.П. Бестужева. – Воронеж: ВГТУ, 2009. – 157 с. 6. Мещерский И.В. Задачи по теоретической механике / И.В. Мещерский. – СПб.: Лань, 2001. 448 с. 7. Сборник заданий для курсовых работ по теоретической механике: учеб. пособие для техн. вузов / под ред. А.А. Яблонского. – М.: Интеграл-Пресс, 2006. 384 с. содержание
Программа курса. . . . . . . . . . . . . . . . . . . . . . . . 1 Динамика. . . . . . . . . . . . . . . . . . . . . . . . . . 1 Динамика точки . . . . . . . . . . . . . . . . . . . . . . 1 Содержание контрольных заданий, выбор вариантов, порядок выполнения работ, общие пояснения к тексту задач . . . . . . . . . . . . . . . . . 5 Принятые обозначения . . . . . . . . . . . . . . . . . . . . 7 Задачи к контрольным заданиям . . . . . . . . . . . . . . 10 Динамика. Задача Д1 . . . . . . . . . . . . . . . . . . 10 Задача Д2 . . . . . . . . . . . . . . . . . . . 16 Задача Д3 . . . . . . . . . . . . . . . . . . . 23 Контрольные вопросы . . . . . . . . . . . . . . . . . . . . 29 Библиографический список . . . . . . . . . . . . . . . . . 30
Программа, методические указания и контрольное задание № 2 (динамика) по дисциплине «Теоретическая механика» для бакалавров всех направлений заочной и заочной ускоренной форм обучения
Составители: Переславцева Наталья Сергеевна Бестужева Наталья Петровна
В авторской редакции
Компьютерный набор Н.С. Переславцевой
Подписано к изданию 30.10.2012. Уч.-изд. л. 1,8.
ФГБОУ ВПО «Воронежский государственный технический университет» 394026 Воронеж, Московский просп., 14 12 |



 массой
массой  , получив в точке
, получив в точке  начальную скорость
начальную скорость  , движется в изогнутой трубе
, движется в изогнутой трубе  , расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0–Д1.9, табл. Д1).
, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0–Д1.9, табл. Д1).



 , Н
, Н , Н
, Н , м
, м , с
, с , Н
, Н







 на груз кроме силы тяжести действуют постоянная сила
на груз кроме силы тяжести действуют постоянная сила  (ее направление показано на рисунках) и сила сопротивления среды
(ее направление показано на рисунках) и сила сопротивления среды  , зависящая от скорости
, зависящая от скорости  груза (направлена против движения).В точке
груза (направлена против движения).В точке  груз, не изменяя своей скорости, переходит на участок
груз, не изменяя своей скорости, переходит на участок  трубы, где на него кроме силы тяжести действует переменная сила
трубы, где на него кроме силы тяжести действует переменная сила  , проекция которой
, проекция которой  задана в таблице.
задана в таблице. или время
или время  , где
, где  .
. . Эта скорость будет начальной для движения груза на участке
. Эта скорость будет начальной для движения груза на участке  , и полагая в этот момент
, и полагая в этот момент  . При интегрировании уравнения движения на участке
. При интегрировании уравнения движения на участке  участка, целесообразно перейти к переменному
участка, целесообразно перейти к переменному  , учтя, что
, учтя, что .
. Пример Д1.
Пример Д1. трубы (рис. Д1) на груз
трубы (рис. Д1) на груз  , где
, где  , до точки
, до точки  равно
равно  . На наклонном участке
. На наклонном участке  на груз действуют сила тяжести, сила трения скольжения с коэффициентом
на груз действуют сила тяжести, сила трения скольжения с коэффициентом  и переменная сила
и переменная сила  , заданная в ньютонах.
, заданная в ньютонах. и
и  и составляем дифференциальное уравнение движения груза в проекции на эту ось:
и составляем дифференциальное уравнение движения груза в проекции на эту ось: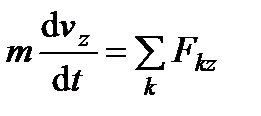 , или,
, или,  . (1)
. (1)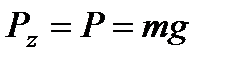 ,
,  . Подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что
. Подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что  , получим
, получим , или
, или  . (2)
. (2) м–1,
м–1,  м2/с2, (3)
м2/с2, (3) м2/с2. Тогда уравнение (2) можно представить в виде:
м2/с2. Тогда уравнение (2) можно представить в виде: . (4)
. (4) и
и  . (5)
. (5)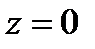
 и из равенства (5) находим
и из равенства (5) находим 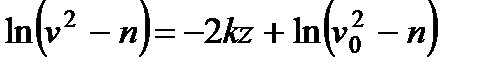 или
или  . Отсюда
. Отсюда и
и  .
.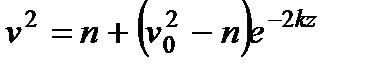 . (6)
. (6) м, и заменяя
м, и заменяя  и
и  их значениями (3), определим скорость ив груза в точке
их значениями (3), определим скорость ив груза в точке  (
(  м/с, число
м/с, число  ):
): и
и  м/с. (7)
м/с. (7) . Найденная скорость
. Найденная скорость  будет для движения на этом участке начальной скоростью (
будет для движения на этом участке начальной скоростью (  ). Изображаем груз (в произвольном положении) и действующие на него силы
). Изображаем груз (в произвольном положении) и действующие на него силы  ,
,  и
и  . Проведем из точки
. Проведем из точки  и
и 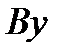 и составим дифференциальное уравнение движения груза в проекции на ось
и составим дифференциальное уравнение движения груза в проекции на ось 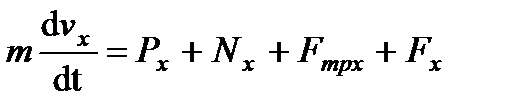 ,
, , (8)
, (8)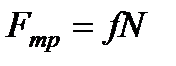 . Для определения
. Для определения  составим уравнение в проекции на ось
составим уравнение в проекции на ось  , получим
, получим  , откуда
, откуда  . Следовательно,
. Следовательно,  . Кроме того,
. Кроме того,  и уравнение (8) примет вид:
и уравнение (8) примет вид: . (9)
. (9) и
и  , подставим эти значения в (9). Тогда получим:
, подставим эти значения в (9). Тогда получим: . (10)
. (10) и интегрируя, найдем:
и интегрируя, найдем: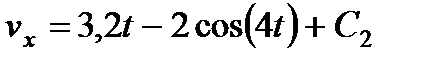 . (11)
. (11) , считая в этот момент
, считая в этот момент  . Тогда при
. Тогда при 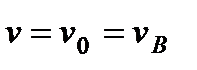 , где
, где  дается равенством (7). Подставляя эти величины в (11), получим
дается равенством (7). Подставляя эти величины в (11), получим .
. уравнение (11) дает:
уравнение (11) дает: . (12)
. (12) . (13)
. (13) , то
, то  и окончательно искомый закон движения груза будет
и окончательно искомый закон движения груза будет . (14)
. (14) – в метрах,
– в метрах,  – в секундах.
– в секундах. м,
м,  м,
м,  м и
м и  м. Массу шкивов считать равномерно распределенной по внешнему ободу. Коэффициент трения грузов о плоскость
м. Массу шкивов считать равномерно распределенной по внешнему ободу. Коэффициент трения грузов о плоскость  .
.


 ,
, 
 ,
,  , м
, м





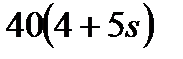











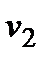
 точки ее приложения, система приходит в движение из состояния покоя. При движении на шкивы действуют постоянные моменты
точки ее приложения, система приходит в движение из состояния покоя. При движении на шкивы действуют постоянные моменты  или
или  сил сопротивления (от трения в подшипниках).
сил сопротивления (от трения в подшипниках). и
и  – скорости грузов 1, 2 и центра масс тела 3 соответственно,
– скорости грузов 1, 2 и центра масс тела 3 соответственно, 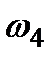 и
и  – угловые скорости тел 4 и 5.
– угловые скорости тел 4 и 5.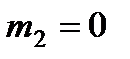 ; остальные тела должны изображаться и тогда, когда их масса равна нулю.
; остальные тела должны изображаться и тогда, когда их масса равна нулю. системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении
системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении  для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение
для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение  , учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
 кг,
кг,  кг,
кг,  кг,
кг,  кг,
кг,  кг,
кг,  м,
м,  м,
м,  м,
м,  ,
,  Н/м,
Н/м, 
 ,
,  Н,
Н,  м.
м. в тот момент времени, когда
в тот момент времени, когда  .
. ,
,  ,
,  ,
,  ,
,  , реакции
, реакции  ,
,  ,
,  ,
,  , натяжение нити
, натяжение нити  , силы трения
, силы трения  ,
,  и момент
и момент  .
. . (1)
. (1) и
и  . Так как в начальный момент система находилась в покое, то
. Так как в начальный момент система находилась в покое, то  . Величина
. Величина  равна сумме энергий всех тел системы:
равна сумме энергий всех тел системы: . (2)
. (2) ,
, ,
, , (3)
, (3) . Для этого предварительно заметим, что
. Для этого предварительно заметим, что  , где
, где  – любая точка обода радиуса
– любая точка обода радиуса  шкива 3 и что точка
шкива 3 и что точка  – мгновенный центр скоростей катка 1, радиус которого обозначим
– мгновенный центр скоростей катка 1, радиус которого обозначим 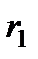 . Тогда
. Тогда ,
,  . (4)
. (4) ,
,  . (5)
. (5) . (6)
. (6) – перемещение груза 5 (
– перемещение груза 5 (  ),
),  и
и  ,
, ,
, ,
, ,
, .
.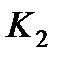 , где приложены силы
, где приложены силы  По условиям задачи,
По условиям задачи,  . Тогда
. Тогда  , где
, где  – перемещение точки
– перемещение точки  (конца пружины). Величины
(конца пружины). Величины  . Для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, так как
. Для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, так как  (равенство
(равенство  уже отмечалось), то и
уже отмечалось), то и  .
.
 . (7)
. (7)
 . (8)
. (8) с–1.
с–1.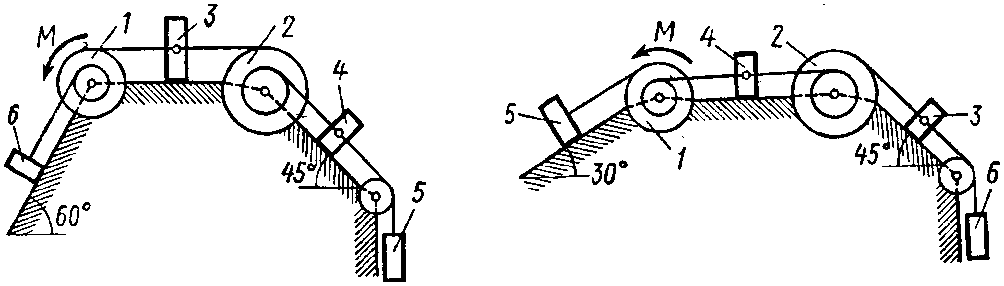




 , приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны:
, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны:  м,
м,  м, шкива 2 –
м, шкива 2 –  м,
м,  м; их радиусы инерции относительно осей вращения равны соответственно
м; их радиусы инерции относительно осей вращения равны соответственно  м и
м и  м.
м. шкивов и грузов заданы в таблице. Грузы, веса которых равны нулю, на чертеже можно не изображать (шкивы 1, 2 изображать всегда как части системы).
шкивов и грузов заданы в таблице. Грузы, веса которых равны нулю, на чертеже можно не изображать (шкивы 1, 2 изображать всегда как части системы).
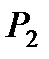





 , характеризующую перемещение этого груза. Для составления уравнения Лагранжа необходимо найти кинетическую энергию
, характеризующую перемещение этого груза. Для составления уравнения Лагранжа необходимо найти кинетическую энергию  системы и выразить все входящие в нее скорости через обобщенную скорость
системы и выразить все входящие в нее скорости через обобщенную скорость  , а затем вычислить обобщенную силу
, а затем вычислить обобщенную силу  . Для этого надо сообщить системе возможное (малое) перемещение, при котором выбранная координата
. Для этого надо сообщить системе возможное (малое) перемещение, при котором выбранная координата  , и составить уравнение работ всех сил на этом перемещении. Коэффициент при
, и составить уравнение работ всех сил на этом перемещении. Коэффициент при  и ступенчатого шкива 2 (радиусы ступеней
и ступенчатого шкива 2 (радиусы ступеней 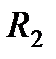 и
и  , радиус инерции относительно оси вращения
, радиус инерции относительно оси вращения  ), и из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом
), и из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом  , приложенной к блоку 1.
, приложенной к блоку 1.
 Н,
Н,  Н,
Н,  Н,
Н,  Н,
Н, 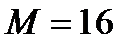
 ,
,  груза 3, полагая, что он движется вниз и отсчитывая
груза 3, полагая, что он движется вниз и отсчитывая  в сторону движения (рис. Д3). Составим уравнение Лагранжа:
в сторону движения (рис. Д3). Составим уравнение Лагранжа: . (1)
. (1) . (2)
. (2) ,
,  ,
,  . (3)
. (3) ,
,  и
и  выразим через обобщенную скорость
выразим через обобщенную скорость  :
: ,
,  ,
,  . (4)
. (4) ,
,  и
и  в соотношение (2), получим:
в соотношение (2), получим: . (5)
. (5) ,
, ,
,  . (6)
. (6)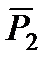 ,
,  ,
,  и пару сил с моментом
и пару сил с моментом 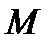 . Сообщим системе возможное перемещение
. Сообщим системе возможное перемещение 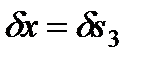 и составим выражение для суммы работ:
и составим выражение для суммы работ: .
. через
через  :
: .
. . (7)
. (7) .
.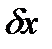 в (7) и будет обобщенной силой:
в (7) и будет обобщенной силой: . (8)
. (8) .
. м/с2.
м/с2. м/с2, знак минус указывает, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рисунке.
м/с2, знак минус указывает, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рисунке. ?
?