 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Теория с примерами (кратко)
Задача 4 Однофакторный эксперимент. Равномерный симметричный план (РСП) Теория с примерами (кратко) 1. Однофакторное ортогонализированное уравнение регрессии второго порядка, в котором все 3 фактора  ортогональны, имеет вид ортогональны, имеет вид  . (1) . (1)
2. Ортогонализирующий коэффициент  для ортогонализации квадратичного фактора для ортогонализации квадратичного фактора  рассчитывается по формуле ( рассчитывается по формуле ( 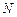 – число опытов) – число опытов)  . для РСП (2) . для РСП (2)
3. Для расчета ортогонализирующего коэффициента  , коэффициентов уравнения регрессии , коэффициентов уравнения регрессии  и их доверительных интервалов и их доверительных интервалов  для РСП можно использовать формулы: для РСП можно использовать формулы: 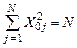 , (3) , (3)
 . (4) . (4)
 . (5) . (5)
4. Натуральные значения фактора  заданы на отрезке заданы на отрезке  . Взаимосвязь нормированных значений фактора Х1 с натуральными х1 определяется следующими формулами: . Взаимосвязь нормированных значений фактора Х1 с натуральными х1 определяется следующими формулами:  ; (6) ; (6)
 ; (7) ; (7)
 ; (8) ; (8)
 , (9) , (9)
где  – основной уровень, интервал варьирования, максимальное и минимальное натуральные значения фактора х1, соответственно. Из уравнений (6) – (9) следует, что если – основной уровень, интервал варьирования, максимальное и минимальное натуральные значения фактора х1, соответственно. Из уравнений (6) – (9) следует, что если  , то , то  . . 5. Матрица планирования (МП) – таблица для построения однофакторного ортогонализированного уравнения регрессии второго порядка, состоящая из N опытов с числом дублей n в каждом опыте, включает в себя столбцы:  . Значения . Значения  (значение параметра Y в j-ом опыте и в i-ом дубле) позволяют провести предварительную обработку экспериментальных данных: расчет выборочных средних (значение параметра Y в j-ом опыте и в i-ом дубле) позволяют провести предварительную обработку экспериментальных данных: расчет выборочных средних  и выборочных дисперсий и выборочных дисперсий  в каждом опыте, проверку выборочных дисперсий на однородность по критерию Кохрена, расчёт дисперсии воспроизводимости в каждом опыте, проверку выборочных дисперсий на однородность по критерию Кохрена, расчёт дисперсии воспроизводимости  и её числа степеней свободы и её числа степеней свободы  . Число опытов . Число опытов 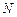 должно быть больше числа коэффициентов уравнения регрессии. Число опытов должно быть больше числа коэффициентов уравнения регрессии. Число опытов  позволяет рассчитать все 3 коэффициента однофакторного ортогонализированного уравнения регрессии второго порядка и обеспечивает надежную проверку уравнения регрессии на адекватность. позволяет рассчитать все 3 коэффициента однофакторного ортогонализированного уравнения регрессии второго порядка и обеспечивает надежную проверку уравнения регрессии на адекватность. Для построения однофакторного ортогонализированного уравнения регрессии второго порядка будем создавать МП на базе равномерного симметричного плана (РСП), в котором натуральные значения варьируются на равноотстоящих друг от друга уровнях:  , ,  . (10) . (10)
С учётом уравнений (6) – (9) нормированные значения фактора  на базе РСП имеют следующие значения: на базе РСП имеют следующие значения:  , ,  . (11) . (11)
NB!Нормированные значения фактора  зависят только от числа опытов N и не зависят от интервала варьирования натурального значения фактора зависят только от числа опытов N и не зависят от интервала варьирования натурального значения фактора 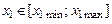 5.1. Предварительная обработка экспериментальных данных в МП на базе РСП для N ‑ опытов  и n – дублей в каждом опыте и n – дублей в каждом опыте  . . 5.1.1 Расчёт выборочных параметров: ‑ выборочное среднее  в каждом опыте в каждом опыте  , ,  ; (12) ; (12)
‑ выборочная дисперсия  в каждом опыте в каждом опыте  , ,  . (13) . (13)
5.1.2. Проверка выборочных дисперсий на однородность по критерию Кохрена при условии, что объём всех выборок одинаковый  : : ‑ экспериментальное значение критерия Кохрена  равно равно  ; (14) ; (14)
‑ табличное значение критерия Кохрена  , в котором на первом месте стоит число степеней свободы , в котором на первом месте стоит число степеней свободы  максимальной дисперсии, а на втором ‑ число степеней свободы максимальной дисперсии, а на втором ‑ число степеней свободы  , равное числу всех дисперсий при доверительной вероятности, , равное числу всех дисперсий при доверительной вероятности,  выбирается из таблицы приложения 5; выбирается из таблицы приложения 5; ‑ выборочные дисперсии  с вероятностью однородны, если с вероятностью однородны, если  ; (15) ; (15)
‑ выборочные дисперсии  неоднородны, если неоднородны, если  . (16) . (16)
5.1.3. Если число дублей  , то проверку случайных значений выборки на промах и на принадлежность их к нормальному закону распределения можно не производить. , то проверку случайных значений выборки на промах и на принадлежность их к нормальному закону распределения можно не производить.
5.1.4. Если все выборочные дисперсии однородны, то дисперсия воспроизводимости  и ее число степеней свободы и ее число степеней свободы  рассчитывают по формулам: рассчитывают по формулам:  ; (17) ; (17)
 . (18) . (18)
6. Матрица моделирования (ММ) –таблицадля построения однофакторного ортогонализированного уравнения регрессии второго порядка, состоящая из N опытов (  ) с числом дублей n ( ) с числом дублей n ( 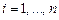 ), включает в себя столбцы ), включает в себя столбцы  , ,  , значения которых позволяют провести окончательную обработку экспериментальных данных: расчет коэффициентов уравнения регрессии , значения которых позволяют провести окончательную обработку экспериментальных данных: расчет коэффициентов уравнения регрессии  и их доверительных интервалов и их доверительных интервалов  , расчёт дисперсии адекватности , расчёт дисперсии адекватности  и её числа степеней свободы и её числа степеней свободы  , проверку уравнения регрессии на адекватность, расчет абсолютной ошибки прогнозирования изучаемого параметра. Столбец нормированного фактора , проверку уравнения регрессии на адекватность, расчет абсолютной ошибки прогнозирования изучаемого параметра. Столбец нормированного фактора  состоит из элементов состоит из элементов  . Столбец нормированных значений фактора . Столбец нормированных значений фактора  в ММ переносятся из МП. в ММ переносятся из МП. 6.1. Так как уравнение регрессии должно состоять только из ортогональных факторов, то прежде чем рассчитывать коэффициенты регрессии и их доверительные интервалы, необходимо убедиться в том, что факторы  взаимно ортогональны (доказать самостоятельно при решении задачи своего варианта). взаимно ортогональны (доказать самостоятельно при решении задачи своего варианта). Определение: факторы  ортогональны, если выполняются равенства: ортогональны, если выполняются равенства:  . (19) . (19)
6.2. Коэффициенты  однофакторного ортогонализированного уравнения регрессии второго порядка однофакторного ортогонализированного уравнения регрессии второго порядка  , с учётом того, что факторы , с учётом того, что факторы  ортогональны, рассчитывают по формулам: ортогональны, рассчитывают по формулам:  ; (20) ; (20)
 . (21) . (21)
 . (22) . (22)
Для расчета коэффициентов  , используя вспомогательные столбцы ММ , используя вспомогательные столбцы ММ  , ,  , ,  , рассчитывают сумма , рассчитывают сумма  , ,  , ,  . Суммы квадратов факторов . Суммы квадратов факторов  , ,  , ,  можно получить прямым подсчетом соответствующих столбцов ММ или по формулам (3) – (5). можно получить прямым подсчетом соответствующих столбцов ММ или по формулам (3) – (5). 6.3. Проверка коэффициентов однофакторного ортогонализированного уравнения регрессии второго порядка на значимость. Дисперсии значимости коэффициентов однофакторного ортогонализированного уравнении регрессии второго порядка при условии, что факторы  ортогональны, рассчитывают по формулам: ортогональны, рассчитывают по формулам:  ; (23) ; (23)
 . (24) . (24)
 . (25) . (25)
6.4. Доверительные интервалы коэффициентов однофакторного ортогонализированного уравнения регрессии второгопорядка  рассчитывают по критерию Стьюдента: рассчитывают по критерию Стьюдента:  ; (26) ; (26)
 ; (27) ; (27)
 ; (28) ; (28)
где  – табличное значение критерия Стьюдента при числе степеней свободы – табличное значение критерия Стьюдента при числе степеней свободы  и доверительной вероятности и доверительной вероятности  выбирается из таблицы приложения 2. выбирается из таблицы приложения 2. 6.5. Коэффициенты однофакторного ортогонализированного уравнения регрессии второго порядка значимы, если выполняются следующие неравенства:  ; (29) ; (29)
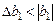 ; (30) ; (30)
 . (31) . (31)
Регрессионный коэффициент, для которого указанное неравенство не выполняется, следует исключить из полученного уравнения регрессии. 6.6. Проверка однофакторного ортогонализированного уравнения регрессии второго порядка на адекватность. Дисперсия адекватности  и её число степеней свободы и её число степеней свободы  для однофакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по формулам: для однофакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по формулам:  ; (32) ; (32)
 ; (33) ; (33)
 ; (34) ; (34)
где 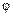 – остаточная сумма квадратов; N – число опытов; n – число дублей в каждом опыте; – остаточная сумма квадратов; N – число опытов; n – число дублей в каждом опыте;  ( (  ) – расчётные значения параметра Y по однофакторному ортогонализированного уравнению регрессии второго порядка ) – расчётные значения параметра Y по однофакторному ортогонализированного уравнению регрессии второго порядка  , в котором только значимые коэффициенты; В – число значимых коэффициентов однофакторного уравнения регрессии второго порядка. , в котором только значимые коэффициенты; В – число значимых коэффициентов однофакторного уравнения регрессии второго порядка. Проверка однофакторного ортогонализированного уравнения регрессии любогопорядка на адекватность сводится к проверке дисперсий  на однородность по критерию Фишера: на однородность по критерию Фишера: ‑ экспериментальное значение критерия Фишера  (отношение бËльшей дисперсии к мÁньшей) (отношение бËльшей дисперсии к мÁньшей)  ; (35) ; (35)
‑ табличное значение критерия Фишера  , в котором на первом месте стоит число степени свободы , в котором на первом месте стоит число степени свободы  бËльшей дисперсии, а на втором ‑ число степени свободы бËльшей дисперсии, а на втором ‑ число степени свободы  мÁньшей дисперсии, при доверительной вероятности мÁньшей дисперсии, при доверительной вероятности  и выбирается из таблицы приложения 4; и выбирается из таблицы приложения 4; ‑ однофакторное ортогонализированное уравнение регрессии любого порядка адекватно, если  ; (36) ; (36)
‑ однофакторное ортогонализированное уравнение регрессии любого порядка неадекватно, если  . (37) . (37)
7. Если полученное однофакторное ортогонализированное уравнение регрессии второго порядка адекватно, то абсолютная погрешность  для параметра для параметра  , рассчитанного по уравнению регрессии , рассчитанного по уравнению регрессии  , равна: , равна:  , (38) , (38)
где  – табличное значение критерия Стьюдента при числе степеней свободы – табличное значение критерия Стьюдента при числе степеней свободы  и доверительной вероятности и доверительной вероятности  выбирается из таблицы приложения 2. выбирается из таблицы приложения 2. 8. Параметр Y, описываемый однофакторным ортогонализированным уравнением регрессии второгопорядка всегда имеет экстремум: максимумпри 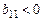 , или минимумпри , или минимумпри 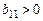 . Необходимое условие максимума (минимума) – равенство нулю первой производной – . Необходимое условие максимума (минимума) – равенство нулю первой производной – 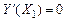 , Продифференцировав однофакторное ортогонализированное уравнение регрессии второго порядка , Продифференцировав однофакторное ортогонализированное уравнение регрессии второго порядка  по фактору X1 и приравняв к нулю первую производную по фактору X1 и приравняв к нулю первую производную 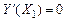 , получим следующее уравнение для расчета оптимального значения фактора X1 , получим следующее уравнение для расчета оптимального значения фактора X1  , (39) , (39)
откуда  . (40) . (40)
Соответствующее натуральное значение фактора  рассчитывается по уравнению (7) рассчитывается по уравнению (7)  . (41) . (41)
Максимум (минимум) параметра  и предельная абсолютная погрешность и предельная абсолютная погрешность 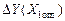 рассчитываются по уравнениям (1) и (40) рассчитываются по уравнениям (1) и (40)  ; (42) ; (42)
 . (43) . (43)
Типовая задача Цель: освоить методы моделирования и оптимизации однофакторных технических систем, описываемых стохастическими закономерностями. Формулировка задачи. Зерно, собранное комбайном, имеет влажность » 30 %. На току оно подсыхает до влажности » 20 %. Для долгосрочного хранения на элеваторе зерно должно иметь влажность 14 %. Для сушки зерна до указанной влажности используют специальные сушила, теплоносителем в которых является горячий воздух. Важнейшим параметром, характеризующим эффективность работы сушила, является удельный расход энергии (параметр Y, кВт×ч/т).При прочих равных условиях удельный расход энергии зависит от температуры теплоносителя (фактор х1, °С). Необходимо изучить зависимость удельного расхода энергии Y от температуры теплоносителя х1, варьируемого в интервале  и определить оптимальный режим функционирования сушила. и определить оптимальный режим функционирования сушила. Математическая формулировка задачи: 1) построить адекватное уравнение регрессии, отражающее зависимость удельного расхода энергии(Y, кВтч/т) от температуры воздуха (х1, °С); 2) рассчитать оптимальное значение фактора х1(°С), при котором удельный расход энергии Y будет минимальным. Решение задачи начнем с построения однофакторного уравнения регрессии второго порядка на базе РСП с числом опытов  и числом дублей и числом дублей  . Результаты эксперимента приведены в таблице 1. . Результаты эксперимента приведены в таблице 1. Таблица 1. – Экспериментальные данные для РСП | N | х1j, °С | Yj1, кВтч/т | Yj2, кВтч/т | Yj3, кВтч/т | Yj4, кВтч/т | | | 73,5 | 75,3 | 73,5 | 74,1 | | | 60,4 | 60,2 | 63,7 | 61,5 | | | 55,4 | 59,0 | 58,8 | 54,8 | | | 54,8 | 55,5 | 54,3 | 51,9 | | | 59,7 | 62,5 | 57,9 | 57,8 | План решения задачи 1. Внимательно прочитать условия задачи. 2. Написать формулы взаимосвязи натуральных значений фактора х1 с нормированными Х1. 3. Создать МПдля построенияоднофакторного ортогонализированного уравнения регрессии второго порядка и выполнить предварительную обработку экспериментальных данных. 4. Создать ММдля построения однофакторного ортогонализированного уравнения регрессии второго порядка и выполнить окончательную обработку экспериментальных данных. 5. В случае адекватности однофакторного ортогонализированного уравнения регрессии второго порядка провести оптимизацию изучаемого объекта: рассчитать оптимальные значения факторов  и и  , значение , значение  , а также абсолютную ошибку , а также абсолютную ошибку  . . 6. По результатам моделирования и оптимизации изучаемой технической системы сделать вывод. NB! Все промежуточные расчеты проводить с точностью не менее 4-х значащих цифр. Решение задачи по плану 1. Пункт 1 выполнить самостоятельно. 2. Уровни и интервал варьирования фактора, а также формулы перевода натуральных x1 в нормированные X1 и обратно приведены в таблице 2 (см. уравнения (6) ‑ (9)). Таблица 2. – Уровни и интервалs варьирования факторов x1 и X1 | Факторы | x1, °С | X1 | | Верхний уровень | x1 max = 120 | + 1 | | Нижний уровень | x1 min = 60 | ‑ 1 | | Основной уровень | x10 = 90 | | | Интервал варьирования | Dx1 = 30 | ‑ | | Формулы взаимосвязи натуральных значений фактора x1 с нормированными X1 |  ; ;  | 3. Создадим МП для построения однофакторного уравнения регрессии второго порядка, которая состоит из столбцов: N,  , , 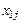 , ,  (из таблицы 1), (из таблицы 1),  , ,  (таблица 3). (таблица 3). Рассчитаем нормированные значения фактора  (см. уравнения (11)). Например, для (см. уравнения (11)). Например, для   ; ;
для   ; ;
Значения факторов для  рассчитайте самостоятельно и внесите в таблицу 3.. рассчитайте самостоятельно и внесите в таблицу 3.. Таблица 3. МПдля построения однофакторного ортогонализированногоуравнения регрессии второго порядка на базе РСП с числом опытов  . Результаты предварительной обработки экспериментальных данных . Результаты предварительной обработки экспериментальных данных | N |  | 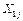 | Yj1, кВтч/т | Yj2, кВтч/т | Yj3, кВтч/т | Yj4, кВтч/т |  |  | | | ‑ 1,0 | 73,5 | 75,3 | 73,5 | 74,1 | 74,10 | 0,7200 | | | ‑ 0,5 | 60,4 | 60,2 | 63,7 | 61,5 | 61,45 | 2,5767 | | | | 55,4 | 59,0 | 58,8 | 54,8 | 57,00 | 4,8800 | | | 0,5 | 54,8 | 55,5 | 54,3 | 51,9 | 54,13 | 2,4425 | | | 1,0 | 59,7 | 62,5 | 57,9 | 57,8 | 59,48 | 4,8292 |  |  |  , , 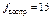 |  | 3.1.Методика эксперимента. Для повышения точности эксперимента температура воздуха  в сушиле поддерживалась на требуемом уровне с точностью в сушиле поддерживалась на требуемом уровне с точностью  . Все остальные факторы (объёмный расход, влажность воздуха и линейная скорость обдува зерна) поддерживались на фиксированных, одинаковых уровнях для всех опытов. Зерно сушилось до влажности . Все остальные факторы (объёмный расход, влажность воздуха и линейная скорость обдува зерна) поддерживались на фиксированных, одинаковых уровнях для всех опытов. Зерно сушилось до влажности  . Если влажность зерна на выходе из сушила превышала 14 %, то скорость конвейерной ленты уменьшалась, если влажность зерна становилась меньше 14 %, то скорость конвейерной ленты увеличивалась. Каждые 2 ч по счетчику электроэнергии с относительной погрешностью 0,1 % определялась величина электроэнергии, затраченной на работу сушила (энергия на подогрев воздуха, энергия на работу компрессора для обдува зерна, энергия двигателя на движение конвейерной ленты). За тот же период измерялась масса высушенного зерна с относительной погрешностью 0,1 %. Параметр . Если влажность зерна на выходе из сушила превышала 14 %, то скорость конвейерной ленты уменьшалась, если влажность зерна становилась меньше 14 %, то скорость конвейерной ленты увеличивалась. Каждые 2 ч по счетчику электроэнергии с относительной погрешностью 0,1 % определялась величина электроэнергии, затраченной на работу сушила (энергия на подогрев воздуха, энергия на работу компрессора для обдува зерна, энергия двигателя на движение конвейерной ленты). За тот же период измерялась масса высушенного зерна с относительной погрешностью 0,1 %. Параметр  при заданной температуре теплоносителя определялся как отношение величины затраченной электроэнергии (кВт×ч) за 2 часа к массе высушенного зерна (т) за этот же период. За смену (8 ч) при заданной температуре теплоносителя параметр при заданной температуре теплоносителя определялся как отношение величины затраченной электроэнергии (кВт×ч) за 2 часа к массе высушенного зерна (т) за этот же период. За смену (8 ч) при заданной температуре теплоносителя параметр  определялся 4 раза определялся 4 раза  . Полностью изучение зависимости параметра . Полностью изучение зависимости параметра  от температуры теплоносителя от температуры теплоносителя  осуществлялась в течение 5 дней (число опытов осуществлялась в течение 5 дней (число опытов  ) при температурах 60, 75, 90, 105 и 120 °С. ) при температурах 60, 75, 90, 105 и 120 °С. 3.2. Проведем предварительную обработку экспериментальных данных (результаты расчета внесены в таблицу 3): 3.2.1.выборочное среднее в каждом опыте  (см. уравнение (12)). Например, выборочное среднее в третьем опыте (см. уравнение (12)). Например, выборочное среднее в третьем опыте 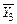 ( (  ) равно ) равно  . .
3.2.2. выборочная дисперсия в каждом опыте  (см. уравнение (13)). Например, выборочная дисперсия в третьем опыте (см. уравнение (13)). Например, выборочная дисперсия в третьем опыте  ( (  ) равна ) равна 
 . .
3.2.3. однородность выборочных дисперсий по критерию Кохрена: ‑ экспериментальное значение критерия Кохрена Gэ (см. уравнения (14))  ; ;
‑ табличное значение критерия Кохрена  при числах степеней свободы при числах степеней свободы  , ,  при доверительной вероятности при доверительной вероятности  выбирается из таблицы приложения 5 выбирается из таблицы приложения 5  . .
Вывод: выборочные дисперсии однородны, так как  (см. уравнение (15)). (см. уравнение (15)). Так какчисло дублей  , то проверку случайных значений каждого опыта на промах и на принадлежность их к нормальному закону распределения проводить не будем (см. пункт 5.3). , то проверку случайных значений каждого опыта на промах и на принадлежность их к нормальному закону распределения проводить не будем (см. пункт 5.3). 3.2.4. Дисперсия воспроизводимости  и её число степеней свободы и её число степеней свободы  (см. уравнения (17), (18)) (см. уравнения (17), (18))  ; ;
 . .
4. Создадим ММ для построения однофакторного ортогонализированного уравнения регрессии второго порядка на базе РСП с числом опытов  (см. таблицу 3). (см. таблицу 3). 4.1. Создадим ММ(таблица 4) для построения однофакторного ортогонализированного уравнения регрессии второго порядка  . ММсодержит столбцы . ММсодержит столбцы  , ,  (см. таблицу 3). Ортогонализирующий коэффициент (см. таблицу 3). Ортогонализирующий коэффициент  (см. уравнение 2). (см. уравнение 2). Таблица 4. – ММ для построения однофакторного ортогонализированного уравнения регрессиивторого порядка на базе РСП с числом опытов  . Результаты окончательной обработки экспериментальных данных . Результаты окончательной обработки экспериментальных данных | N | X0j | X1j |  | 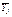 | 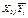 |  |  |  |  | | | – 1,0 | 0,50 | 74,10 | 74,10 | – 74,10 | 37,05 | 73,92 | 0,0324 | | | – 0,5 | ‑ 0,25 | 61,45 | 61,45 | – 30,725 | ‑ 15,36 | 62,21 | 0,5776 | | | | ‑ 0,50 | 57,00 | 57,00 | 0,00 | ‑ 28,50 | 55,87 | 1,2769 | | | 0,5 | ‑ 0,25 | 54,13 | 54,13 | 27,065 | ‑ 13,53 | 54,90 | 0,5929 | | | 1,0 | 0,50 | 59,48 | 59,48 | 59,48 | 29,74 | 59,30 | 0,0324 |  | | 2,8 | 0,875 | 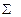 | 306,2 | ‑ 18,28 | 9,395 |  |  |  | 61,24 | ‑ 7,312 | 10,74 |  , ,  | 4.2. Проверим факторы  на ортогональность (см. уравнение (19)) на ортогональность (см. уравнение (19))  ; ;
 ; ;

4.3. Рассчитаем коэффициенты  однофакторного ортогонализированного уравнения регрессии второго порядка однофакторного ортогонализированного уравнения регрессии второго порядка  (результаты расчета внести в таблицу 4). (результаты расчета внести в таблицу 4). Образуем столбцы  и рассчитаем их суммы: и рассчитаем их суммы:   ; ;
 ; ;
 . .
Суммы квадратов  , ,  , ,  рассчитаем по формулам (3) – (5). рассчитаем по формулам (3) – (5). 4.4. Рассчитаем коэффициенты однофакторного ортогонализированного уравнения регрессии второго порядка  (см. уравнения (20) ‑ (21)) (см. уравнения (20) ‑ (21))  ; ;
 ; ;
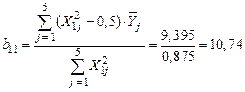 . .
4.5. Проверим коэффициенты  однофакторного ортогонализированного уравнения регрессии второго порядка на значимость по критерию Стьюдента: однофакторного ортогонализированного уравнения регрессии второго порядка на значимость по критерию Стьюдента: ‑ дисперсии значимости коэффициентов регрессии  (см. уравнения (23) – (25)) (см. уравнения (23) – (25))  ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
‑ доверительные интервалы коэффициентов  однофакторного ортогонализированного уравнения регрессии второго порядка однофакторного ортогонализированного уравнения регрессии второго порядка  (см. уравнения (26) – (28): (см. уравнения (26) – (28):  ; ;
 ; ;
 . .
где  – табличное значение критерия Стьюдента при числе степеней свободы – табличное значение критерия Стьюдента при числе степеней свободы  и доверительной вероятности и доверительной вероятности  выбирается из таблицы приложения 2 выбирается из таблицы приложения 2 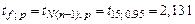 ; ;
‑ регрессионные коэффициента  значимы, так как (см. уравнения (29) – (31)) значимы, так как (см. уравнения (29) – (31))  ; ;
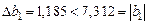 ; ;

Вывод: однофакторное ортогонализированное уравнение регрессии второго порядка, в котором все коэффициенты значимы, имеет вид  . .
4.6. Проверим однофакторное ортогонализированное уравнение регрессиивторогопорядка  на адекватность по критерию Фишера: на адекватность по критерию Фишера: ‑ расчетное значение  в каждом опыте определяется по однофакторному ортогонализированному уравнению регрессии второго порядка в каждом опыте определяется по однофакторному ортогонализированному уравнению регрессии второго порядка  . Например, для . Например, для   ; ;
‑ образуем столбец 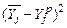 и рассчитаем его значения. Например, для и рассчитаем его значения. Например, для   ; ;
‑ остаточная сумма квадратов 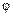 рассчитывается по уравнению (34) рассчитывается по уравнению (34) 
 ; ;
‑ дисперсия адекватности  и её число степеней свободы и её число степеней свободы  (см. уравнения (32), (33)) (см. уравнения (32), (33))  ; ;
 ; ;
‑ экспериментальное значение критерия Фишера Fэ (см. уравнение (35))  , так как , так как  ; ;
‑ табличное значение критерия Фишера  , в котором на первом месте стоит число степени свободы , в котором на первом месте стоит число степени свободы  бËльшей дисперсии, а на втором ‑ число степени свободы бËльшей дисперсии, а на втором ‑ число степени свободы  мÁньшей дисперсии, при доверительной вероятности мÁньшей дисперсии, при доверительной вероятности  выбирается из таблицы приложения 4 выбирается из таблицы приложения 4  . .
6. Оптимизация изучаемой технической системы. 6.1. Параметр  имеет минимум, так как имеет минимум, так как 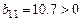 : : ‑ оптимальное значение фактора  (см. уравнение (40)) (см. уравнение (40))  . .
Оптимальное значение фактора  (см. уравнение (41) и данные таблицы 2)) (см. уравнение (41) и данные таблицы 2))  . .
‑ минимальное значение параметра Ymin (см. уравнение (42)):  
6.2. Абсолютная погрешность  параметра параметра  , значение которого рассчитывается по однофакторному ортогонализированному уравнению регрессии второго порядка , значение которого рассчитывается по однофакторному ортогонализированному уравнению регрессии второго порядка  , определим по уравнению (43) , определим по уравнению (43) 
 кВт·ч/т. кВт·ч/т.
С учетом полученных значений  корректно оформим результаты расчета корректно оформим результаты расчета  (раздел 1.1, п. 3): (раздел 1.1, п. 3):  ; ;
 ; ;
 ; ;

7. Окончательный вывод. Однофакторное ортогонализированное уравнение регрессии второго порядка со значимыми регрессионными коэффициентами  адекватно описывает процесс сушки зерна. Минимальные энергозатраты при сушке зерна при температуре воздуха адекватно описывает процесс сушки зерна. Минимальные энергозатраты при сушке зерна при температуре воздуха  составляют составляют 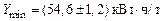 . . Ответ. 1) Ортогонализированное однофакторное уравнение регрессии второго порядка  . .
±0,8 ±1,2 ±2,0  ; ;  ; ;  ; ;  . .
Уравнение регрессии второго порядка адекватно, так как  ; ; 2) Оптимальные параметры:  ; ;  ; ;  . . Контрольные вопросы 1. Написать в общем виде однофакторное ортогонализированное уравнение регрессии второго порядка. 2. Написать формулы взаимосвязи нормированных Х1 и натуральных х1 значений фактора. 3. Построить МП на базе РСП с числом опытов N = 21 для построения однофакторного ортогонализированного уравнения регрессии второго порядка. 4. Сформулировать алгоритм проверки выборочных дисперсий на однородность по критерию Кохрена. Как найти табличное значение критерия Кохрена? 5. Написать формулу для расчета дисперсии воспроизводимости и её числа степеней свободы. 6. Написать формулу для расчета ортогонализирующего коэффициента  . . 7. Построить ММ для построения однофакторного ортогонализированного уравнения регрессии второго порядка на базе РСП с числом опытов N = 11. 8. Написать формулы для расчета коэффициентов однофакторного ортогонализированного уравнения регрессии второго порядка. 9. Написать формулы для расчета дисперсий значимости и доверительных интервалов коэффициентов однофакторного ортогонализированного уравнения регрессии второго порядка. Сформулировать критерий проверки коэффициентов уравнения регрессии на значимость. Как найти табличное значение критерия Стьюдента? 10. Написать уравнение для расчёта дисперсии адекватности и её числа степени свободы. 11. Сформулировать алгоритм проверки уравнения регрессии любого порядка на адекватность. Как найти табличное значение критерия Фишера? 12. Написать уравнение для расчета абсолютной погрешности DY(Х1) параметра Y(Х1), рассчитанного по ортогонализированному однофакторному уравнению регрессии второгопорядка. 13. Сформулировать алгоритм оптимизации изучаемого объекта, описываемого ортогонализированным однофакторным уравнением регрессии второгопорядка. Контрольные задачи Таблица 5. – Номера вариантов (N – число опытов; n – число дублей, интервал варьирования фактора  ) ) | 1 вариант (N = 21; n = 4; [60; 100]) | 2 вариант (N = 21; n = 5; [80; 120]) | 3 вариант (N = 21; n = 6; [70; 110]) | | 4 вариант (N = 20; n = 4; [82; 120]) | 5 вариант (N = 20; n = 5; [66; 104]) | 6 вариант (N = 20; n = 6; [76; 114]) | | 7 вариант (N = 19; n = 4; [82; 118]) | 8 вариант (N = 19; n = 5; [64; 100]) | 9 вариант (N = 19; n = 6; [72; 108]) | | 10 вариант (N = 18; n = 4; [82; 116]) | 11 вариант (N = 18; n = 5; [66; 100]) | 12 вариант (N = 18; n = 6; [70; 104]) | | 13 вариант (N = 17; n = 4; [82; 114]) | 14 вариант (N = 17; n = 5; [64; 96]) | 15 вариант (N = 17; n = 6; [70; 102]) | | 16 вариант (N = 16; n = 4; [88; 118]) | 17 вариант (N = 16; n = 5; [60; 120]) | 18 вариант (N = 16; n = 6; [76; 106]) | | 19 вариант (N = 15; n = 4; [88; 116]) | 20 вариант (N = 15; n = 5; [64; 120]) | 21 вариант (N = 15; n = 6; [76; 104]) | | 22 вариант (N = 14; n = 4; [86; 112]) | 23 вариант (N = 14; n = 5; [64; 116]) | 24 вариант (N = 14; n = 6; [78; 104]) | | 25 вариант (N = 13; n = 4; [84; 108]) | 26 вариант (N = 13; n = 5; [70; 118]) | 27 вариант (N = 13; n = 6; [80; 104]) | | 28 вариант (N = 12; n = 4; [82; 104]) | 29 вариант (N = 12; n = 5; [62; 106]) | 30 вариант (N = 12; n = 6; [76; 120]) | | 31 вариант (N = 11; n = 4; [80; 100]) | 32 вариант (N = 11; n = 5; [62; 102]) | 33 вариант (N = 11; n = 6; [80; 120]) | | 34 вариант (N = 10; n = 4; [88; 106]) | 35 вариант (N = 10; n = 5; [60; 114]) | 36 вариант (N = 10; n = 6; [70; 106]) | | 37 вариант (N = 9; n = 4; [82; 98]) | 38 вариант (N = 9; n = 5; [66; 114]) | 39 вариант (N = 9; n = 6; [70; 102]) | | 40 вариант (N = 8; n = 4; [60; 116]) | 41 вариант (N = 8; n =5; [76; 118]) | 42 вариант (N = 8; n = 6; [88; 116]) | | 43 вариант (N = 7; n = 4; [60; 108]) | 44 вариант (N = 7; n = 5; [74; 110]) | 45 вариант (N = 7; n = 6; [90; 114]) | | 46 вариант (N = 6; n = 4; [86; 116]) | 47 вариант (N = 6; n = 5; [60; 100]) | 48 вариант (N = 6; n = 6; [60; 120) | | 49 вариант (N =5; n = 4; [86; 110]) | 50 вариант (N = 5; n = 5; [70; 110]) | 51 вариант (N = 5; n = 6; [60; 116]) | Экспериментальные данные, отражающие зависимость удельного расхода энергии при сушке зерна (параметр Y, кВт×ч/т) от температуры теплоносителя (фактор х1, °С), представлены в таблице 6. Таблица 6. – Результаты эксперимента (фактор х1 – температура теплоносителя, оС; параметр Y – удельный расход энергии, кВт×ч/т) | х1, оС | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | | 76.3 | 79.4 | 79.3 | 76.4 | 76.0 | 76.2 | | 72.5 | 75.2 | 72.8 | 72.4 | 69.8 | 74.9 | | 72.0 | 64.1 | 70.1 | 70.4 | 69.1 | 69.2 | | 69.6 | 65.9 | 70.2 | 64.2 | 69.3 | 66.6 | | 65.1 | 64.0 | 68.2 | 67.0 | 69.1 | 67.6 | | 60.9 | 63.8 | 60.9 | 60.2 | 62.4 | 63.5 | | 61.8 | 62.4 | 60.6 | 62.8 | 61.8 | 57.4 | | 55.3 | 58.6 | 59.2 | 59.7 | 60.6 | 57.8 | | 55.6 | 58.2 | 58.8 | 55.4 | 56.5 | 58.3 | | 55.6 | 55.1 | 55.7 | 54.2 | 57.4 | 57.7 | | 55.2 | 53.4 | 54.7 | 54.4 | 58.3 | 52.8 | | 55.6 | 54.4 | 51.8 | 53.5 | 53.1 | 51.3 | | 49.9 | 52.8 | 51.7 | 50.9 | 54.6 | 54.2 | | 52.3 | 52.4 | 52.5 | 50.9 | 50.3 | 53.4 | | 52.3 | 51.3 | 50.8 | 50.4 | 52.3 | 51.4 | | 48.8 | 50.3 | 50.7 | 50.7 | 54.7 | 47.5 | | 49.9 | 48.0 | 51.9 | 51.3 | 48.5 | 49.5 | | 47.4 | 46.4 | 50.1 | 50.3 | 49.9 | 49.8 | | 51.7 | 51.8 | 50.8 | 51.6 | 51.4 | 49.8 | | 52.3 | 49.2 | 49.8 | 47.4 | 49.0 | 52.8 | | 50.1 | 50.8 | 51.0 | 51.4 | 52.4 | 50.5 | | 52.3 | 51.9 | 52.1 | 51.7 | 50.1 | 50.1 | | 51.2 | 51.6 | 53.2 | 49.4 | 54.2 | 53.6 | | 53.6 | 54.9 | 54.4 | 53.8 | 54.8 | 53.0 | | 56.7 | 53.6 | 55.8 | 54.1 | 53.4 | 51.6 | | 55.2 | 55.7 | 56.4 | 57.6 | 60.6 | 58.5 | | 54.8 | 56.1 | 58.0 | 58.0 | 58.3 | 58.2 | | 61.9 | 56.5 | 59.3 | 59.1 | 60.3 | 59.9 | | 62.4 | 61.2 | 59.7 | 62.8 | 60.7 | 57.8 | | 66.4 | 62.7 | 63.4 | 64.0 | 60.7 | 62.0 | | 64.3 | 65.3 | 66.1 | 65.8 | 65.0 | 63.0 | Примечание.Для получения исходных данных следует действовать следующим образом. Допустим, например, Вы решаете вариант № 41. Для этого варианта число опытов N = 8, число дублей n = 5, интервал варьирования фактора  ) (см. таблицу 5). Необходимо сначала построить матрицу планирования эксперимента (см., например, таблицу 3). Для этого по уравнениям (10) – (11) следует рассчитать значения ) (см. таблицу 5). Необходимо сначала построить матрицу планирования эксперимента (см., например, таблицу 3). Для этого по уравнениям (10) – (11) следует рассчитать значения  . Следующий этап – выбрать первые(!) 5 дублей для каждого значения фактора . Следующий этап – выбрать первые(!) 5 дублей для каждого значения фактора  . . | х1, оС | Y1 | Y2 | Y3 | Y4 | Y5 | | 55.6 | 58.2 | 58.8 | 55.4 | 56.5 | |
| ©2015 www.megapredmet.ru Все права принадлежат авторам размещенных материалов. |




 ортогональны, имеет вид
ортогональны, имеет вид . (1)
. (1) для ортогонализации квадратичного фактора
для ортогонализации квадратичного фактора  рассчитывается по формуле (
рассчитывается по формуле ( 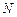 – число опытов)
– число опытов) . для РСП (2)
. для РСП (2) и их доверительных интервалов
и их доверительных интервалов  для РСП можно использовать формулы:
для РСП можно использовать формулы: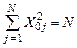 , (3)
, (3) . (4)
. (4) . (5)
. (5) заданы на отрезке
заданы на отрезке  . Взаимосвязь нормированных значений фактора Х1 с натуральными х1 определяется следующими формулами:
. Взаимосвязь нормированных значений фактора Х1 с натуральными х1 определяется следующими формулами: ; (6)
; (6) ; (7)
; (7) ; (8)
; (8) , (9)
, (9) – основной уровень, интервал варьирования, максимальное и минимальное натуральные значения фактора х1, соответственно. Из уравнений (6) – (9) следует, что если
– основной уровень, интервал варьирования, максимальное и минимальное натуральные значения фактора х1, соответственно. Из уравнений (6) – (9) следует, что если  , то
, то  .
. . Значения
. Значения  (значение параметра Y в j-ом опыте и в i-ом дубле) позволяют провести предварительную обработку экспериментальных данных: расчет выборочных средних
(значение параметра Y в j-ом опыте и в i-ом дубле) позволяют провести предварительную обработку экспериментальных данных: расчет выборочных средних  и выборочных дисперсий
и выборочных дисперсий  в каждом опыте, проверку выборочных дисперсий на однородность по критерию Кохрена, расчёт дисперсии воспроизводимости
в каждом опыте, проверку выборочных дисперсий на однородность по критерию Кохрена, расчёт дисперсии воспроизводимости  и её числа степеней свободы
и её числа степеней свободы  . Число опытов
. Число опытов  позволяет рассчитать все 3 коэффициента однофакторного ортогонализированного уравнения регрессии второго порядка и обеспечивает надежную проверку уравнения регрессии на адекватность.
позволяет рассчитать все 3 коэффициента однофакторного ортогонализированного уравнения регрессии второго порядка и обеспечивает надежную проверку уравнения регрессии на адекватность. ,
,  . (10)
. (10) на базе РСП имеют следующие значения:
на базе РСП имеют следующие значения: ,
,  зависят только от числа опытов N и не зависят от интервала варьирования натурального значения фактора
зависят только от числа опытов N и не зависят от интервала варьирования натурального значения фактора 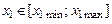
 и n – дублей в каждом опыте
и n – дублей в каждом опыте  .
. в каждом опыте
в каждом опыте ,
,  ,
,  :
: равно
равно ; (14)
; (14) , в котором на первом месте стоит число степеней свободы
, в котором на первом месте стоит число степеней свободы  максимальной дисперсии, а на втором ‑ число степеней свободы
максимальной дисперсии, а на втором ‑ число степеней свободы  , равное числу всех дисперсий при доверительной вероятности,
, равное числу всех дисперсий при доверительной вероятности,  выбирается из таблицы приложения 5;
выбирается из таблицы приложения 5; с вероятностью однородны, если
с вероятностью однородны, если ; (15)
; (15) . (16)
. (16) , то проверку случайных значений выборки на промах и на принадлежность их к нормальному закону распределения можно не производить.
, то проверку случайных значений выборки на промах и на принадлежность их к нормальному закону распределения можно не производить. ; (17)
; (17) . (18)
. (18)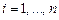 ), включает в себя столбцы
), включает в себя столбцы  ,
,  , значения которых позволяют провести окончательную обработку экспериментальных данных: расчет коэффициентов уравнения регрессии
, значения которых позволяют провести окончательную обработку экспериментальных данных: расчет коэффициентов уравнения регрессии  и их доверительных интервалов
и их доверительных интервалов  , расчёт дисперсии адекватности
, расчёт дисперсии адекватности  и её числа степеней свободы
и её числа степеней свободы  , проверку уравнения регрессии на адекватность, расчет абсолютной ошибки прогнозирования изучаемого параметра. Столбец нормированного фактора
, проверку уравнения регрессии на адекватность, расчет абсолютной ошибки прогнозирования изучаемого параметра. Столбец нормированного фактора  состоит из элементов
состоит из элементов  . Столбец нормированных значений фактора
. Столбец нормированных значений фактора  взаимно ортогональны (доказать самостоятельно при решении задачи своего варианта).
взаимно ортогональны (доказать самостоятельно при решении задачи своего варианта). . (19)
. (19) , с учётом того, что факторы
, с учётом того, что факторы  ; (20)
; (20) . (21)
. (21) . (22)
. (22) ,
,  ,
,  , рассчитывают сумма
, рассчитывают сумма  ,
,  ,
,  . Суммы квадратов факторов
. Суммы квадратов факторов  ,
,  ,
,  можно получить прямым подсчетом соответствующих столбцов ММ или по формулам (3) – (5).
можно получить прямым подсчетом соответствующих столбцов ММ или по формулам (3) – (5). ; (23)
; (23) . (24)
. (24) . (25)
. (25) ; (26)
; (26) ; (27)
; (27) ; (28)
; (28) – табличное значение критерия Стьюдента при числе степеней свободы
– табличное значение критерия Стьюдента при числе степеней свободы  и доверительной вероятности
и доверительной вероятности  ; (29)
; (29)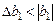 ; (30)
; (30) . (31)
. (31) ; (32)
; (32) ; (33)
; (33) ; (34)
; (34)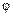 – остаточная сумма квадратов; N – число опытов; n – число дублей в каждом опыте;
– остаточная сумма квадратов; N – число опытов; n – число дублей в каждом опыте;  (
(  , в котором только значимые коэффициенты; В – число значимых коэффициентов однофакторного уравнения регрессии второго порядка.
, в котором только значимые коэффициенты; В – число значимых коэффициентов однофакторного уравнения регрессии второго порядка. на однородность по критерию Фишера:
на однородность по критерию Фишера: (отношение бËльшей дисперсии к мÁньшей)
(отношение бËльшей дисперсии к мÁньшей) ; (35)
; (35) , в котором на первом месте стоит число степени свободы
, в котором на первом месте стоит число степени свободы  бËльшей дисперсии, а на втором ‑ число степени свободы
бËльшей дисперсии, а на втором ‑ число степени свободы  мÁньшей дисперсии, при доверительной вероятности
мÁньшей дисперсии, при доверительной вероятности  ; (36)
; (36) . (37)
. (37) для параметра
для параметра  , рассчитанного по уравнению регрессии
, рассчитанного по уравнению регрессии  , (38)
, (38)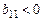 , или минимумпри
, или минимумпри 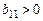 . Необходимое условие максимума (минимума) – равенство нулю первой производной –
. Необходимое условие максимума (минимума) – равенство нулю первой производной – 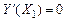 , Продифференцировав однофакторное ортогонализированное уравнение регрессии второго порядка
, Продифференцировав однофакторное ортогонализированное уравнение регрессии второго порядка  по фактору X1 и приравняв к нулю первую производную
по фактору X1 и приравняв к нулю первую производную  , (39)
, (39) . (40)
. (40) рассчитывается по уравнению (7)
рассчитывается по уравнению (7) . (41)
. (41) и предельная абсолютная погрешность
и предельная абсолютная погрешность 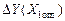 рассчитываются по уравнениям (1) и (40)
рассчитываются по уравнениям (1) и (40) ; (42)
; (42) . (43)
. (43) и определить оптимальный режим функционирования сушила.
и определить оптимальный режим функционирования сушила. и числом дублей
и числом дублей  . Результаты эксперимента приведены в таблице 1.
. Результаты эксперимента приведены в таблице 1. и
и  , а также абсолютную ошибку
, а также абсолютную ошибку  .
. ;
; 
 ,
, 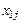 ,
,  (из таблицы 1),
(из таблицы 1),  ,
, 
 ;
;
 ;
; рассчитайте самостоятельно и внесите в таблицу 3..
рассчитайте самостоятельно и внесите в таблицу 3.. . Результаты предварительной обработки экспериментальных данных
. Результаты предварительной обработки экспериментальных данных
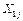




 ,
, 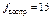

 . Все остальные факторы (объёмный расход, влажность воздуха и линейная скорость обдува зерна) поддерживались на фиксированных, одинаковых уровнях для всех опытов. Зерно сушилось до влажности
. Все остальные факторы (объёмный расход, влажность воздуха и линейная скорость обдува зерна) поддерживались на фиксированных, одинаковых уровнях для всех опытов. Зерно сушилось до влажности  . Если влажность зерна на выходе из сушила превышала 14 %, то скорость конвейерной ленты уменьшалась, если влажность зерна становилась меньше 14 %, то скорость конвейерной ленты увеличивалась. Каждые 2 ч по счетчику электроэнергии с относительной погрешностью 0,1 % определялась величина электроэнергии, затраченной на работу сушила (энергия на подогрев воздуха, энергия на работу компрессора для обдува зерна, энергия двигателя на движение конвейерной ленты). За тот же период измерялась масса высушенного зерна с относительной погрешностью 0,1 %. Параметр
. Если влажность зерна на выходе из сушила превышала 14 %, то скорость конвейерной ленты уменьшалась, если влажность зерна становилась меньше 14 %, то скорость конвейерной ленты увеличивалась. Каждые 2 ч по счетчику электроэнергии с относительной погрешностью 0,1 % определялась величина электроэнергии, затраченной на работу сушила (энергия на подогрев воздуха, энергия на работу компрессора для обдува зерна, энергия двигателя на движение конвейерной ленты). За тот же период измерялась масса высушенного зерна с относительной погрешностью 0,1 %. Параметр  при заданной температуре теплоносителя определялся как отношение величины затраченной электроэнергии (кВт×ч) за 2 часа к массе высушенного зерна (т) за этот же период. За смену (8 ч) при заданной температуре теплоносителя параметр
при заданной температуре теплоносителя определялся как отношение величины затраченной электроэнергии (кВт×ч) за 2 часа к массе высушенного зерна (т) за этот же период. За смену (8 ч) при заданной температуре теплоносителя параметр  . Полностью изучение зависимости параметра
. Полностью изучение зависимости параметра 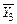 (
(  ) равно
) равно .
. (см. уравнение (13)). Например, выборочная дисперсия в третьем опыте
(см. уравнение (13)). Например, выборочная дисперсия в третьем опыте  (
( 
 .
. ;
; ,
,  при доверительной вероятности
при доверительной вероятности  .
. (см. уравнение (15)).
(см. уравнение (15)). ;
; .
. ,
,  (см. таблицу 3). Ортогонализирующий коэффициент
(см. таблицу 3). Ортогонализирующий коэффициент  (см. уравнение 2).
(см. уравнение 2).
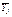
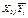





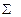



 ,
, 
 ;
; ;
;
 (результаты расчета внести в таблицу 4).
(результаты расчета внести в таблицу 4). и рассчитаем их суммы:
и рассчитаем их суммы:
 ;
; ;
; .
. ,
,  ,
,  рассчитаем по формулам (3) – (5).
рассчитаем по формулам (3) – (5). ;
; ;
;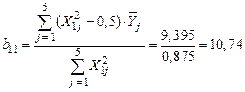 .
. (см. уравнения (23) – (25))
(см. уравнения (23) – (25)) ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. и доверительной вероятности
и доверительной вероятности 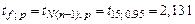 ;
; ;
;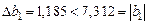 ;
;
 .
. . Например, для
. Например, для  ;
;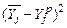 и рассчитаем его значения. Например, для
и рассчитаем его значения. Например, для  ;
;
 ;
; ;
; ;
; , так как
, так как  ;
; , в котором на первом месте стоит число степени свободы
, в котором на первом месте стоит число степени свободы  бËльшей дисперсии, а на втором ‑ число степени свободы
бËльшей дисперсии, а на втором ‑ число степени свободы  мÁньшей дисперсии, при доверительной вероятности
мÁньшей дисперсии, при доверительной вероятности  .
.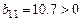 :
: (см. уравнение (40))
(см. уравнение (40)) .
. .
.

 , определим по уравнению (43)
, определим по уравнению (43)
 кВт·ч/т.
кВт·ч/т. корректно оформим результаты расчета
корректно оформим результаты расчета  ;
; ;
; ;
;
 адекватно описывает процесс сушки зерна. Минимальные энергозатраты при сушке зерна при температуре воздуха
адекватно описывает процесс сушки зерна. Минимальные энергозатраты при сушке зерна при температуре воздуха  составляют
составляют 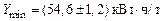 .
. .
. ;
;  ;
;  ;
;  .
. ;
; ;
;  ;
;  .
. .
. )
) ) (см. таблицу 5). Необходимо сначала построить матрицу планирования эксперимента (см., например, таблицу 3). Для этого по уравнениям (10) – (11) следует рассчитать значения
) (см. таблицу 5). Необходимо сначала построить матрицу планирования эксперимента (см., например, таблицу 3). Для этого по уравнениям (10) – (11) следует рассчитать значения  . Следующий этап – выбрать первые(!) 5 дублей для каждого значения фактора
. Следующий этап – выбрать первые(!) 5 дублей для каждого значения фактора  .
.