 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Метод конечного использования (метод доходов). 12
ЗАДАЧИ Задача 1. Рассчитать розничную цену товара при условии, что затраты на сырье и материалы составили 6310 руб, энергию - 475 руб., оплату труда с отчислениями– 780 руб., прочие расходы – 235 руб, коммерческие расходы – 161 руб. Уровень рентабельности продукции составляет 25%, НДС 18%, торговая надбавка – 16 %.
Решение Полная себестоимость производства товара составляет: 6310+475+780+235 + 161= 7961 руб. Прибыль в составе цены : 7961*25% = 1990 руб. Цена изготовителя: 7961+1990 = 9951 руб. НДС: 9951 * 18% = 1791 руб. Торговая надбавка: 9951 * 16% = 1592 руб. Розничная цена: 9951+1791+1592 = 13334 руб. Ответ: розничная цена товара составит 13334 рублей.
Задача 2. Организация на условиях скользящих цен получила заказ на поставку оборудования. Предложенные поставщиком условия определяют следующую раскладку цены на составляющие: стоимость материалов – 50%; стоимость рабочей силы – 30%; постоянные расходы – 10%; коммерческие расходы – 10%. За период исполнения заказа цены на материалы выросли на 17%, ставки заработной платы в отрасли повысились на 5%, коммерческие расходы снизились на 6%. Приняв базисную цену за 9300 условных денежных единиц, определить цену контракта к моменту исполнения заказа.
Решение Для расчета используем метод установления цены с учетом инфляции: Ц1 = 9300 * ( 0,5*1,17 + 0,3 * 1,05 + 0,1 * 0,94 + 0,1) = 9300 * 1,094 = 10174 руб. Ответ: к моменту исполнения договора цена контракта составит 10174 рублей.
Задача 3 На отраслевом рынке функционируют пять фирм-продавцов. Рыночные доли, приходящиеся на каждого из участников отраслевого рынка, распределены следующим образом: фирма А – 0,52 ; фирма В -0,24; фирма С -0,11; фирма D -0,08; фирма Е -0,05. Рассчитать индекс Херфиндаля-Хиршмана и определить тип отраслевого рынка.
Решение:
Поскольку значение HHI находится в пределах от 0,18 до 1, то данный тип рынка имеет высококонцентрированную структуру (концентрация на рынке высокая).
ЗАДАЧА 4 Определить величину основного платежа за четвертый год, если выдана ссуда размером 1 000 000 000 сроком на 5 лет под 12% годовых. Решение Для основных платежей по займу, который погашается равными платежами в конце или начале каждого расчетного периода, в MS Excel XP используется функция: ОСПЛТ(Ставка, Период, Кпер, Пс, Бс) В нашем случае функция ОСПЛТ имеет вид: ОСПЛТ(12%, 4, 5,1000000000) Ввод данных и расчеты производятся в соответствии с рисунком 7.1.
Рисунок 7.1 - Расчет основных платежей по займу В ячейку В8 вводится формула: =ОСПЛТ(В5;В6;В4;ВЗ) ЗАДАЧА 5 Рассчитать 20-летнюю ипотечную ссуду со ставкой 10% годовых при начальном взносе 25% и ежемесячной (ежегодной) выплате. Решение Для вычисления величины постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке используется функция ПЛТ: ПЛТ (Ставка; Клер; Бс; Пс; Тип) В нашем случае функция ПЛТ имеет вид: а) ПЛТ(10%/12;20*12; -(350000*(1-25%))) - ежемесячные выплаты; б) ПЛТ(10%;20,-(350000*(1-25%))) - ежегодные выплаты. Решение задачи приведено на рисунках 7.2 и 7.3.
Рисунок 7.2 - Расчет ипотечной ссуды
Рисунок 7.3 - Формулы для расчета ипотечной суды ЗАДАЧА 6 Определить, какая сумма окажется на банковском счете, если 52 000 рублей положены на 20 лет под 11% годовых. Проценты начисляются ежемесячно. Решение Для расчета будущей стоимости единой суммы вклада используются сложные проценты, а расчетная формула основана на функции БС: БС(Ставка; Кпер; Плт; Пс; Тип) Для нашей задачи функция БС примет вид: БС{11%/12;20*12;;-52000) Решение задачи приведено на рисунке 7.4, а формула для ячейки В8: =БС(B4/B5;B6*B5;;-B3) Аналогичным образом можно использовать встроенные функции MS Excel и для других финансовых расчетов. Приведем еще несколько примеров. ЗАДАЧА 7 Ожидается, что ежегодные доходы от реализации проекта составят 54 000 000 руб. Рассчитать срок окупаемости проекта, если инвестиции к началу поступления доходов составят 140 000 000 руб., а норма дисконтирования 7,67%. Решение Для определения срока платежа используется функция КПЕР(Ставка; Плт; Пс; Бс; Тип), которая в нашей задаче выглядит следующим образом: КПЕР(7,67%; 54000000; -140000000) = 3
Рисунок 7.4 - Расчет будущей стоимости вклада ЗАДАЧА 8 Облигация номиналом 200 000 руб. выпущена на 7 лет. Предусматривается следующий порядок начисления процентов: в первый год - 11%, последующие три года - по 16%, в оставшиеся три года - по 20%. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке. Решение Для расчета наращенной стоимости облигации по сложной процентной ставке используется функция: БЗРАСПИС(Первичное; План) Для нашей задачи функция принимает вид: ВЗРАСПИС(200000; {11%; 16%; 16%; 16%; 20%; 20%; 20%}) Решение приведено на рисунке 7.5, а формула для расчета в ячейке В67: =БЗРАСПИС(B3;B7:B13)
Рисунок 7.5 - Расчет наращенной стоимости облигации посложной процентной ставке ЗАДАЧА 9 Затраты по проекту составят 600 млн. руб. Ожидаемые доходы в течение последующих 5 лет составят, соответственно, 50, 100, 300, 200, 300 млн. руб. Оценить экономическую целесообразность проекта по скорости оборота инвестиции, если рыночная норма дохода 15%. Решение Для вычисления внутренней скорости оборота инвестиции (внутренней нормы доходности) используется функция ВСД: ВСД (Значения; Предположения) В нашем случае функция для решения задачи использует только аргумент Значения, один из которых обязательно отрицателен. Если внутренняя скорость оборота инвестиций будет больше рыночной нормы доходности, то проект считается экономически целесообразным. В противном случае проект должен быть отвергнут. Решение приведено на рис. 7.6. Формулы для расчета: а) в ячейке В84: =ВСД(B3:B9) б) в ячейке С84: =ЕСЛИ(B12>B11;"Проект экономически целесообразен"; "Проект необходимо отвергнуть")
Рисунок 7.6 - Расчет внутренней скорости оборота инвестиций
Задача 10. С использованием метода экстраполяции определить базовый вариант прогноза доли продукции высокотехнологичных и наукоемких отраслей в ВВП на 2017 г. (ВК-4) Таблица 1 – Прогнозирование удельного веса продукции высокотехнологичных и наукоемких отраслей в ВВП, %
Рисунок 1 – Тенденции удельного веса продукции высокотехнологичных и наукоемких отраслей в ВВП, %
Ответ: 22,0%, поскольку максимальное значение R2 у степенной линии тренда
Задача11. Определить эффективность работы предприятия по показателю рентабельности продукции, если известно, что в I квартале объем производства составлял 125 изделий, во II кв. он увеличился на 7%, а в III кв. он уменьшился на 4% по сравнению с I кв. Постоянные затраты не менялись и их общая сумма равна 1500 руб., что составляет 10% от себестоимости продукции в I кв., 17% от себестоимости продукции во II кв. и 8% от себестоимости продукции в III кв. Цена продукции в I кв. –98 руб., во II – 105 руб., в III кв. – 90 руб. Решение задачи представить в виде таблицы:
Задача12. Определить эффективность работы предприятия по показателю рентабельности продукции, если известно, что в I квартале объем производства составлял 125 изделий, во II кв. он увеличился на 7%, а в III кв. он уменьшился на 4% по сравнению с I кв. Постоянные затраты не менялись и их общая сумма равна 1500 руб., что составляет 10% от себестоимости продукции в I кв., 17% от себестоимости продукции во II кв. и 8% от себестоимости продукции в III кв. Цена продукции в I кв. –98 руб., во II – 105 руб., в III кв. – 90 руб. Решение задачи представить в виде таблицы:
Решение задачи:
Задача 13. Распределение работников на предприятии по размеру заработной ежедневной платы характеризуется следующими данными:
Определите среднюю месячную заработную плату, среднюю модальную и медианную заработную плату. Решение: 1.Среднюю заработную плату на предприятии определим по формуле средней арифметической взвешенной, для вычисления которой подготовим расчётную таблицу. Таблица – Исходные и расчётные данные для вычисления средней зарплаты
Данные из таблицы подставим в формулу и вычислим искомую среднюю заработную плату:
2) Определим модальную и медианную ежедневную заработную плату. Для этого сначала необходимо установить модальный интервал (интервал с наибольшей частотой), а затем вычислим: а) МОДАЛЬНУЮ заработную плату определим по формуле:
Для определения модального интервала находим максимальную частоту, в данной задаче это значение 53. Ей соответствует интервал заработной платы 800–1100 руб. Подставляем все значения в формулу моды:
где: Х0 – нижняя граница модального интервала; i – величина интервала; f1 – частота интервала, предшествующего модальному; f2 – частота модального интервала; f3 – частота интервала, следующего за модальным. б) МЕДИАННУЮ заработную плату по формуле:
Где: Х0 – нижняя граница медианного интервала;
Так как сумма частот (числа работников) равна 180, то полусумма частот 90. По принципу накопления частот суммируем их до тех пор, пока не «перешагнем» середину, т.е. значение 90. Таким образом, медианный интервал по условию данной задачи 800-1100 руб. в день. Подставим все значения в формулу. Расчет показал уровень медианной заработной платы в размере 3) Выводы: Получили среднюю ежедневную заработную плату 991,67 руб/день, среднюю модальную заработную плату 982,61 руб/день и среднюю медианную заработную плату 992,45 руб/ день. Задача 14. Имеются данные о себестоимости объемов производства продукции на предприятии.
Определить: Индивидуальные и общие индексы себестоимости, индивидуальный и общий индекс физического объема продукции, индивидуальный и общий индекс затрат на производство. Покажите взаимосвязь общих индексов. Сделать выводы. Решение: Порядок выполнения задачи: 1. Индивидуальные индексы себестоимости по отдельным видам продукции рассчитываются отношением себестоимости в отчетном периоде к базисной себестоимости, т.е.: – по продукции А – по продукции Б –по продукции В Аналогично рассчитаем индивидуальные индексы физического объема продукции:
– по продукции А –по продукции Б –по продукции В Дополнительно для удобства рассчитаем три колонки (общая себестоимость всей продукции):
2) Вычислим общий индекс себестоимости:
2) Определим общий индекс физического объема продукции:
3) Рассчитаем общий индекс затрат:
4) Взаимосвязь рассчитанных индексов выглядит следующим образом:
1,0109=1,1184*0,90389 1,0109=1,0109 – расчеты произведены верно. 5) Выводы: индивидуальные индексы себестоимости по всем видам продукции показывают увеличение на 12,3, 17,5 и 4,5% соответственно. По показателю физического объема продукции индексы показывают снижение по продукции видов А и Б (на 16,9 и 5,4%), а по продукции В – увеличение на 2,0%. Взаимосвязь рассчитанных общих индексов проверена.
Задача 15: ООО «Заря» необходимо обосновать экономическуюэффективностьприродоохранных мероприятий на основе критерия чистого дисконтированного дохода (ЧДД) и срока окупаемости инвстиций, если известно, что годовая величина предотвращаемого данными мероприятиями ущерба составляет 50 тыс. руб. в год, и появляется, начиная с третьего года их реализации. Капитальные затраты на реализацию мероприятий составляют: в первый год - 80 тыс. руб., во второй год - 60 тыс. руб. Ставка дисконтирования – 10%. Решение: Поскольку социальные и экологические мероприятия предполагают льготное оценивание, то в качестве коэффициента дисконтирования следует принять величину, равную 0,5 банковской ставки, т.е. 5%. Результаты расчета ЧДД представлены в табл. 1.
Значение ЧДД меняет знак с минуса на плюс между 5-м и 6-м годами (см. табл. 1). Следовательно, срок окупаемости составляет пять лет и несколько месяцев. Для более точного расчета следует воспользоваться вышеприведенной формулой, в соответствии с которой получаем:
Задание16. Фирма АВС планирует открыть производство и реализацию макаронных изделий в г. №-ске. По данным маркетинговых исследований установлено, что на рынке сбыта макаронных изделий города № - ска представлено 3 организации, производящих продукцию для местного потребления. На основе анкетирования потребителей данной продукции выявлены свойства, которым потребитель отдает предпочтение при приобретении изделия и установлена степень важности каждого фактора для потребителей (табл.1). Провести экспертную оценку конкурентоспособности предприятия по отношению к каждому конкуренту и выявить основного конкурента.
Таблица 1 - Факторы конкурентоспособности
Таблица 2 –Оценка конкурентоспособности предприятия
Ответ.Основным конкурентом является ООО «АВС».Сильной позицией предприятия является высокое качество продукции и хорошая репутация в глазах потенциальных покупателей.
ЗАДАЧА 17: Методом цепных подстановок определить влияния факторов на исходную функцию (себестоимость продукции). S — себестоимость товара — рассчитывается как сумма затрат на его производство:S= Смат +L + Copr + Cyпp. Смат — затраты на материалы, L — оплата труда рабочих, С — организационные расходы и Супр — расходы на управление. Причем все затраты берутся в процентном отношении к затратам на материалы: L — 20 %; Сорг — 10 %; Супр — 15 %. По плану затраты на материалы должны были составить 20 тыс. руб. Однако на практике удалось уменьшить затраты на материалы, и они составили 16 тыс. руб. Задание: 1. Определить плановую себестоимость продукции; 2. Рассчитать фактическую себестоимость продукции; 3. Выявить отклонение фактической себестоимости от плановой и определить за счет влияния каких факторов. Решение: 1. Определим плановую себестоимость продукции по формуле S= Смат +L + Copr + Cyпp. Смат=20 тыс. руб. L=4 тыс. руб. Copr=2 тыс. руб. Супр=3 тыс. руб. S= Смат +L + Copr + Cyпp=20+4+2+3=29 тыс. руб. Плановая себестоимость составила 29 тыс. рублей. 2.Рассчитаем фактическую себестоимость продукции: S= Смат +L + Copr + Cyпp=16+3,2+1,6+2,4=23,2 тыс. руб. Фактическая себестоимость составила 23,2 тысячи рублей. 3. Выявим отклонение фактической себестоимости от плановой: · снижение затрат на материалы: 29-25=4 тыс. руб. · снижение затрат на оплату труда:25-24,2=0,8 тыс. руб. · уменьшение организационных расходов: 24,2-23,8=0,4 тыс. руб. · уменьшение управленческих расходов: 23,8-23,2=0,6 тыс. руб.
Задача18 1. По данным 26 муниципальных районов Ставропольского края о стоимости продукции сельского хозяйства (Y) и стоимости основных фондов (Х) были получены следующие параметры и меры статистической корректности парных уравнений регрессий следующих видов:
В соответствии с полученными результатами моделирования сделайте вывод о наиболее приемлемой форме модели для описания представленной зависимости; опишите зависимость между признаками; охарактеризуйте качество модели. Решение. В соответствии с величиной коэффициента корреляции R связь между переменными во всех формах модели можно охарактеризовать, используя шкалу Чеддока, как высокую, прямую. При этом максимальное значение было получено для линейной формы зависимости (0,77). В соответствии с величиной коэффициента детерминации R2 можно сделать вывод о доли вариации результативного показателя Y, вызванной вариацией факторного признака X. Таким образом, вариация стоимости продукции сельского хозяйства (Y) по синтезированной модели парной линейной регрессии на 59,29 % объясняется изменением стоимости основных фондов сельхозтоваропроизводителей (Х). Для линейного уравнения регрессии значение коэффициента детерминации максимальное. Для оценки статистической значимости полученной модели парной степенной регрессии определено фактическое значение F-критерия Фишера. Для линейной функции оно является максимальным (34,82). Полученное значение сопоставим с табличным критическим значением, которое при уровне значимости 0,05 и соответствующем числе степеней свободы составит 4,26. Так как Для оценки адекватности уравнения регрессии на основе сравнения теоретических и эмпирических уровней результативного показателя на ретроспективном материале используется средняя ошибка аппроксимации A. Для линейной формы связи этот показатель минимален (21,52%). Таким образом, все полученные модели парной регрессии являются статистически значимыми, но наилучшей (с точки зрения полученных характеристик) для описания зависимости стоимости продукции сельского хозяйства (Y) в рассматриваемых районах региона от вариации стоимости основных фондов сельхозтоваропроизводителей (Х) следует признать уравнение парной линейной регрессии, так как для данной модели получена наименьшая величина средней ошибки аппроксимации ( Задача19 2.Для набора переменных было построено уравнение линейной множественной регрессии. При 26 наблюдениях были получены следующие результаты:
Охарактеризуйте полученную модель. Примечание. Y – продукция сельского хозяйства, млн руб.; Х1 – стоимость основных фондов, млн руб.; Х2 – приходится комбайнов на 1000 га посевов шт. Решение. Полученное значение показателя свидетельствует о высокой связи (в соответствии со шкалой Чеддока, так как Синтезированное уравнение линейной множественной регрессии позволило на 59,9 % объяснить изменение y в среднем по в зависимости от вариации х1 и х2. Полученное значение критерия Фишера сравним с табличным критическим значением, которое берется из специальных таблиц при соответствующем уровне значимости и числе степеней свободы (k1 и k2). Для нашей задачи при уровне значимости 0,05 и числе степеней свободы k1= m = 2 и k2= n – (m + 1)= 23 табличное значение F-критерия составит 3,42. Так как На основании полученных частных коэффициентов корреляции можно охарактеризовать взаимосвязь (в соответствии со шкалой Чеддока) между вариацией y и х1, как высокую. Изменение результативной переменной (y) и х2, как слабую. В общей вариации результативной переменной (y), объясненной синтезированной моделью линейной множественной регрессии (59,9 %), на долю факторной переменной х1 приходится 57,4 % и лишь 2,5 % – на долю переменной х2. Задача20 3. На рисунке представлены результаты, полученные средствами Microsoft Excell. Постройте эконометрическую модель, опишите зависимость между переменными; охарактеризуйте качество модели. Примечание. y – финансовые результаты деятельности сельхозпредприятий, млн руб.; х1 – степень износа основных производственных фондов, %; х2 – объем производства зерновых культур, тыс. тонн.
Решение. Полученное уравнение множественной линейной регрессии имеет следующий вид:
Значения коэффициентов регрессии можно охарактеризовать следующим образом: для фактора х1 – увеличение степени износа основных фондов сельскохозяйственных предприятий края на 1 % приводит в среднем по районам края к снижению прибыли предприятий на 2,65013 млн руб.; для фактора х2 – увеличение производства зерна сельскохозяйственными предприятиями края на 1 тыс. тонн приводит к увеличению прибыли предприятий в среднем по районам края на 0,970806 млн руб. В соответствии с полученными результатами можно отметить, что синтезированное уравнение множественной регрессии характеризуется высокой статистической значимостью. Так, на основании величины показателя множественной корреляции (0,708) можно сделать вывод в соответствии со шкалой Чеддока о высокой (так как Однако считается, что если В таблице Дисперсионный анализ по столбцу df приводятся значения числа степеней свободы. На пересечении столбца SS и строки Регрессия находится значение факторной суммы квадратов отклонений, SS и Остаток – остаточной суммы квадратов отклонений, SS и Итого – общей суммы квадратов отклонений. В результате отношения соответствующей суммы квадратов отклонений и числа степеней свободы по столбцу MS получены значения факторной и остаточной дисперсии в расчете на одну степень свободы. Фактическое значение F-критерия показывает, что факторная дисперсия в 11,555 раза превышает остаточную. По столбцу t-статистика приведены фактические значения t-критерия Стьюдента для каждого из коэффициентов регрессии. Для нашего примера незначимым следует считать полученное значение коэффициента регрессии при факторной переменной х2, для него р = 0,156, что больше 0,05. Это означает, что для улучшения качества модели в дальнейшем следовало бы исключить данную переменную из исходной модели. В столбцах Нижние 95 % и Верхние 95 % итоговой таблицы приводятся значения верхних и нижних границ коэффициентов уравнения регрессии с 95-процентной вероятностью. Если в соответствии с ними рассчитать два ряда теоретических значений y по нижним и верхним границам коэффициентов регрессии, то это позволит получить доверительные интервалы вариации рассчитанных по полученному уравнению регрессии значений результативного показателя. В столбце Значимость F приведена вероятность ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную. Существует общепринятая терминология, которая относится к доверительным интервалам вероятности. Высказывания, имеющие вероятность ошибки Таким образом, для нашего примера получен значимый результат (
Задача 21
1. Рассчитать показатели выручки от реализации колбасных изделий по годам реализации проекта.
Решение задачи
Задача 22
2. Заполнить форму баланса продукции растениеводства
Решение задачи Заполнить форму баланса продукции растениеводства
Задача 23. Имеются следующие данные по РФ за 2012г. (в текущих ценах; млрд. руб.):
Величина статистического расхождения составляет 705,0 млрд. руб. Определите объём ВВП (в рыночных ценах) тремя методами.
Решение задачи: Существует три метода определения ВВП: Производственный метод. Оценка валового внутреннего продукта производственным методом получается как сумма валовой добавленной стоимости всех отраслей или институциональных секторов в основных ценах плюс чистые налоги на продукты. Сумма валовой добавленной стоимости определяется как стоимость выпуска минус промежуточное потребление. Чистые налоги на продукты рассчитываются, как любые налоги на продукты за вычетом субсидий на продукты: ВВП = ВВ - ПП + Н – С ВВП = 107956,1 – 54671,6 + 9492,3 – 177,8 = 62599 млрд. руб. Метод конечного использования (метод доходов). Оценка валового внутреннего продукта методом конечного использования получается как сумма расходов на конечное потребление, плюс валовое накопление, плюс экспорт, минус импорт: ВВП= КП+ВН+ (Э - И) Расходы на конечное потребление включают расходы домашних хозяйств, государственных учреждений и некоммерческих организаций, обслуживающих домашние хозяйства. Валовое накопление включает валовое накопление основного капитала, изменение запасов материальных оборотных средств, приобретение ценностей за вычетом выбытия (чистое приобретение ценностей). Итак, ВВП = КП + ВНОК + ΔМОС + ЧПЦ + (Э – И) = 30543,5 + 11664,8 + 263,3 + 13768,0 + 2496,5 + (18428,0 – 13860,1) = 63304 млрд. руб. ВВП, рассчитанный методом конечного использования, отличается от ВВП, рассчитанного производственным методом, на величину статистического расхождения. 12 |
рублей в день
–полусумма всех частот совокупности,
– сумма накопленных частот интервалов предшествующих медианному.
,
, т.е. себестоимость по продукции А увеличилась на 12,3%.
т.е. себестоимость по продукции Б увеличилась на 17,5%.
т.е. себестоимость по продукции Б увеличилась на 4,5%.
т.е. физический объем продукции А снижен на 16,9%
т.е. физический объем продукции Б снижен на 5,4%
т.е. физический объем продукции В увеличился на 2,0%
или 111.84%
или 90.389%
или 101.09%
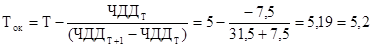
, то делаем вывод о существенности изучаемой связи по линейной модели.
) и наибольшее значение показателей корреляции и детерминации ( 
и 
).
) изменения y от вариации х1 и х2.
, то полученную модель множественной регрессии с вероятностью 95 % можно считать статистически значимой.
.
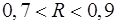) взаимосвязи между уровнем получаемой сельскохозяйственными предприятиями прибыли и факторными показателями: уровнем износа основных фондов и объемом производства зерновой продукции. На основании значения коэффициента множественной детерминации можно утверждать, что факторные показатели модели позволяют на 50,1 % объяснить вариацию уровней доходов СХП края.
, то это говорит о высокой точности аппроксимации (модель хорошо описывает явление); если коэффициент детерминации находится в пределах 
, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если же 
, принято считать, что точность аппроксимации недостаточна (как и в нашем случае) и модель требует улучшения (введения новых независимых переменных, учета нелинейностей и т. д.).
, коэффициент может считаться нулевым, это означает, что влияние соответствующей независимой переменной на зависимую переменную y недостоверно, и эта независимая переменная может быть исключена из уравнения.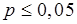
, называются значимыми; высказывания с вероятностью ошибки 
– очень значимыми, а высказывания с вероятностью ошибки 
– максимально значимыми.