 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вопрос 7. Закон Больцмана о равномерном распределении энергии по степеням свободы (закон равнораспределения).
закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы. Если система находится в состоянии термодинамического равновесия, при температуреТ, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы. На каждую поступательную iп и вращательную iвр степени свободы приходится энергия 1/2 kT. Для колебательной iкол, степени свободы она равна kT. Таким образом число степеней свободы i = iп + iвр + 2iкол
для трехатомных молекул:
В общем случае для молярной массы газа
Для произвольного количества газов:
Из теории также следует, что СV не зависит от температуры. Для одноатомных газов это выполняется в очень широких пределах, а для двухатомных газов только в интервале от 100 до 1000 К. Отличие связано с проявлением квантовых законов. При низких температурах вращательное движение как бы «вымерзает» и двухатомные молекулы движутся поступательно, как одноатомные; равны их теплоёмкости.
Вопрос8. Основные понятия термодинамики: внутренняя энергия, работа, количество теплоты. Наряду с механической энергией, любое тело (или система) обладает внутренней энергией. Внутренняя энергия – энергия покоя. Она складывается из теплового хаотического движения молекул, составляющих тело, потенциальной энергии их взаимного расположения, кинетической и потенциальной энергии электронов в атомах, нуклонов в ядрах и так далее. В термодинамике важно знать не абсолютное значение внутренней энергии, а её изменение. В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой энергии недостаточно, чтобы изменить строение атома, а тем более ядра). Следовательно, фактически под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул. Внутренняя энергия U одного моля идеального газа равна:
Таким образом, внутренняя энергия зависит только от температуры. Внутренняя энергия U является функцией состояния системы, независимо от предыстории. Понятно, что в общем случае термодинамическая система может обладать как внутренней, так и механической энергией, и разные системы могут обмениваться этими видами энергии. Обмен механической энергией характеризуется совершенной работой А, а обмен внутренней энергией – количеством переданного тепла Q.Итак, работа и теплота не есть особые формы энергии. Нельзя говорить о запасе теплоты или работы. Это мера переданной другой системе механической или внутренней энергии. Вот о запасе этих энергий можно говорить. Кроме того, механическая энергия может переходить в тепловую энергию и обратно. Во всех случаях, превращение механической энергии в тепловую и обратно совершается всегда в строго эквивалентных количествах. В этом и состоит суть первого начала термодинамики, следующего из закона сохранения энергии. Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и на совершение телом работы:
– это и есть первое начало термодинамики, или закон сохранения энергии в термодинамике. Правило знаков:
– изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы. Выражение (4.1.1) для малого изменения состояния системы будет иметь вид:
В этом выражении U – функция состояния системы; dU – её полный дифференциал, а δQ иδА таковыми не являются. В каждом состоянии система обладает определенным и только таким значением внутренней энергии, поэтому можно записать:
Важно отметить, что теплота Q и работаА зависят от того, каким образом совершен переход из состояния 1 в состояние 2 (изохорически, адиабатически и т.д.), а внутренняя энергия U не зависит. При этом нельзя сказать, что система обладает определенным для данного состояния значением теплоты и работы. Из формулы (4.1.2) следует, что количество теплоты выражается в тех же единицах, что работа и энергия, т.е. в джоулях (Дж). Особое значение в термодинамике имеют круговые или циклические процессы, при которых система, пройдя ряд состояний, возвращается в исходное. На рисунке 4.1 изображен циклический процесс 1–а–2–б–1, при этом была совершена работа А.
Так как U – функция состояния, то
Это справедливо для любой функции состояния. Если Следует отметить, что первое начало термодинамики не указывает, в каком направлении идут процессы изменения состояния, что является одним из его недостатков. |



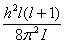

 .
. .
. .
. ,
, .
. энергии, так как при этом есть и кинетическая, и потенциальная энергия, то есть появляется шестая степень свободы – колебательная. При температуре равной 2500 К, молекулы диссоциируют. На диссоциацию молекул тратится энергия раз в десять превышающая среднюю энергию поступательного движения. Это объясняет сравнительно низкую температуру пламени. Кроме того, атом – сложная система, и при высоких температурах начинает сказываться движение электронов внутри него.
энергии, так как при этом есть и кинетическая, и потенциальная энергия, то есть появляется шестая степень свободы – колебательная. При температуре равной 2500 К, молекулы диссоциируют. На диссоциацию молекул тратится энергия раз в десять превышающая среднюю энергию поступательного движения. Это объясняет сравнительно низкую температуру пламени. Кроме того, атом – сложная система, и при высоких температурах начинает сказываться движение электронов внутри него. или
или
 ,
, если тепло передаётся от окружающей среды данной системе,
если тепло передаётся от окружающей среды данной системе,  и
и  если система производит работу над окружающими телами, при этом
если система производит работу над окружающими телами, при этом  . Учитывая правило знаков, первое начало термодинамики можно записать в виде:
. Учитывая правило знаков, первое начало термодинамики можно записать в виде: ,
,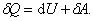
 ,
,
 то согласно первому началу термодинамики
то согласно первому началу термодинамики  , т.е. нельзя построить периодически действующий двигатель, который совершал бы бóльшую работу, чем количество сообщенной ему извне энергии. Иными словами, вечный двигатель первого рода невозможен. Это одна из формулировок первого начала термодинамики.
, т.е. нельзя построить периодически действующий двигатель, который совершал бы бóльшую работу, чем количество сообщенной ему извне энергии. Иными словами, вечный двигатель первого рода невозможен. Это одна из формулировок первого начала термодинамики.