 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА ПРИБОРЕ ОБЕРБЕКА.
Муромский институт (филиал) федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Владимирский государственный университет Имени Александра Григорьевича и Николая Григорьевича Столетовых»
Кафедра: «ФПМ» Дисциплина: Физика
ЛАБОРАТОРНАЯ РАБОТА № 5.02
ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА ПРИБОРЕ ОБЕРБЕКА.
Утверждена на методическом семинаре кафедры ФПМ
Зав. кафедрой_______________
ЛАБОРАТОРНАЯ РАБОТА № 5.02 ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА ПРИБОРЕ ОБЕРБЕКА. Цель работы:изучение вращательного движения и проверка зависимости между угловым ускорением тела, его моментом инерции и моментом внешних сил. Приборы и принадлежности: прибор Обербека, грузы, секундомер, линейка.
К ДОПУСКУ:
1. Изучите устройство и принцип работы прибора. 2. Что такое момент инерции тела относительно оси? Как определить момент инерции прибора Обербека? 3. Что такое момент силы относительно точки? Как определить момент сил, приводящих во вращение прибор? 4. Что такое угловое ускорение? Как оно связано с тангенциальным ускорением? Как измерить ускорение в данной работе? 5. Какое уравнение выражает зависимость между угловым ускорением E тела и моментом силы, действующей на него? 6. Какие измерения прибора и инструменты необходимы для выполнения работы? 7. Какие соотношения необходимо проверить в работе? 8. Какие измерения и в каком порядке необходимо выполнить для проверки необходимых соотношений? 9. Составьте таблицу.
1. ВВЕДЕНИЕ
Вращательным движением твердого тела называется такое движение, при котором остаются неподвижными, по крайней мере, две его точки. Прямая, проходящая через эти две точки, называется осью вращения. Очевидно, что все точки этой прямой также будут неподвижными. Под вращательным движением мы будем понимать вращение вокруг неподвижной оси. При этом все точки тела движутся по окружностям, центры которых лежат на оси вращения, а плоскости этих окружностей перпендикулярны к оси вращения. При вращении тела расстояние от оси вращения не изменяется: rK = const. Вращательное движение тела характеризуется угловой скоростью
где j - угол поворота тела, а также угловым ускорением
Очевидно, что w и Е постоянны для всех точек тела. Зная w и Е, легко найти скорости vK и ускорения
где vK – скорость (k = 1, 2, 3,…) точки тела,
rk – расстояние этой точки от оси вращения. vk, При изучении динамики вращательного движения твердого тела вводятся другие величины: момент импульса L относительно некоторой оси L = J w, (1) кинетическая энергия тела
Здесь J – момент инерции тела относительно оси вращения. Это скалярная величина, равная сумме произведений масс точек тела на квадраты их расстояний до оси вращения.
Из формулы (3) видно, что момент инерции тела – величина аддитивная. Момент инерции тела равен сумме моментов инерции всех его частей. Он зависит от распределения массы в этом теле и от величины массы тела. Тело обладает моментом инерции независимо от того, движется оно или покоится. Для заданной оси J = const. Очевидно, что под действием внешних сил момент импульса L тела относительно оси вращения может изменяться. Изменение L обусловлено моментом внешних сил:
M – главный момент внешних сил относительно оси вращения тела. С учетом (1) имеем
Отсюда получим
Выражения (4) и (5) называются основным уравнением динамики вращательного движения твердого тела. Изучение зависимостей, определенных уравнением (5) является основной задачей в данной работе. Прибор Обербека (рис. 1). На общем валу, закрепленном в подшипниках, взаимно перпендикулярно крепятся четыре стержня одинакового сечения и равной длины, на которых насажены четыре одинаковых груза m, способных перемещаться вдоль стержней. Грузы m могут закрепляться в любом положении на стержнях винтами. С валом жестко закреплен шкив К, на который намотана нить, перетянутая через блок В. На его свободном конце подвешен груз Р массой m. При опускании груза нить сматывается со шкива К и приводит во вращение крестовину. Нить на шкив наматывается в один ряд.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Штангельциркулем измеряют радиус r шкива К. 2. Измеряют расстояние R от центра тяжести грузов m до оси крестовины. 3. Устанавливают грузы m на крестовине так, как указано в соответствующем индивидуальном задании. Вычисляют момент инерции J крестовины по формуле
4. Подвешивают поочередно к свободному концу нити грузы различных масс m1, m2, m3, вычисляют соответствующие ускорения а1, а2, а3 по формуле а= 5. Определяют момент внешних сил М1, М2, М3, приложенных к крестовине по формуле (7). Из рисунка 1 видно, что непосредственно к крестовине приложена сила Для нахождения FH рассмотрим движение груза Р. На основании второго закона Ньютона имеем: m1a = m1g – FH. Отсюда FH = m1(g – a) и M = m1(g – a)r. (7) Зная а, легко вычислить М по формуле (7). 6. Вычисляют угловые ускорения крестовины для каждого значения а1, а2, а3 по формуле Е= Результаты измерений и вычислений заносят в таблицу 1.
Таблица 1
7. Пункты 3 – 6 выполняются при J = const. Согласно (5) для двух значений имеем: JE1 = M1 и JE2 = M2, отсюда
и легко устанавливается зависимость E от М. Сделайте соответствующие выводы. 8. Исследование зависимости E = f(J). К свободному концу нити подвешивают груз Р массой m=0,2кг. Сдвигают грузы на стержнях крестовины как указано в соответствующих индивидуальных заданиях. Вычисляют по (6) изменение значения J. Определяют три раза для трех различных R угловые ускорения крестовины Е1, Е2, Е3. Проверяют справедливость соотношений
9. Результаты измерений и расчетов заносят в таблицу 2.
Таблица 2
Делают выводы.
3. ЗАДАНИЕ К РАБОТЕ
1. Изучить методы измерения момента внешних сил, приложенных к крестовине. 2. Вычислить момент инерции крестовины с грузами по (6). 3. Вычислить угловое ускорение крестовины. 4. Занести в таблицу результаты измерений. 5. Проверить справедливость отношений (9) и (8). Что они выражают? Как их вывести? Сделать выводы.
4. ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ВАРИАНТ 1.
Начинают выполнение работы, когда все 4 груза расположены на концах стержней. Изменение момента инерции достигается перемещением двух грузов на противоположные концы стержней ближе к оси крестовины на 10 – 12 см.
ВАРИАНТ 2.
Начинают выполнение работы, когда все 4 груза расположены у оси крестовины. Изменение момента инерции прибора Обербека достигается перемещением двух противоположных грузов от оси прибора каждый раз на 10 – 12 см.
ВАРИАНТ 3.
Начинают выполнение работы, закрепив два противоположных груза m на концах стержней, а два других – близ оси крестовины. Изменение момента инерции достигается удалением двух противоположных грузов от оси крестовины каждый раз на 10 – 12 см.
ВАРИАНТ 4.
Начинают выполнение работы, когда все 4 груза расположены на 1/3 длины от концов стержней. Изменение момента инерции достигается удалением двух противоположных грузов на концы стержня. Второй раз их приближают к оси крестовины.
ВАРИАНТ 5.
Начинают выполнение работы, когда все 4 груза расположены на 1/3 длины стержней от оси крестовины. Изменение момента инерции достигается сначала перемещением двух противоположных грузов к оси крестовины, а затем их удалением на концы стержней.
ВАРИАНТ 6.
Начинают выполнение работы, когда все 4 груза расположены на середине стержней. Изменение момента инерции достигается перемещением двух грузов сначала к оси крестовины, а затем на концы стержней.
ВАРИАНТ 7. Начинают выполнение работы, когда все 4 груза расположены на 1/4 длины стержней от оси крестовины. Изменяют момент инерции перемещением двух противоположных грузов сначала на концы стержней, а затем к оси крестовины.
ВАРИАНТ 8.
Начинают выполнение работы, когда грузы расположены на 1/4 длины стержней от оси крестовины. Изменяют момент инерции сначала удалением двух противоположных грузов на конце стержней, а в другой раз два других груза располагают на 1/4 длины от конца стержней.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется моментом силы относительно точки? 2. Что такое момент инерции твердого тела относительно оси? Какова роль момента инерции во вращательном движении? 3. Что называется моментом импульса твердого тела относительно оси? 4. Что называется угловым ускорение тела? 5. Выведите основное уравнение динамики вращательного движения. 6. Выведите формулы работы и мощности сил, приложенных к твердому телу при вращательном движении. 7. Сформулируйте закон сохранения момента сил импульса в случае вращательного движения. 8. Как вычислить главный момент внешних сил, приложенных к механической системе относительно оси?
ЛИТЕРАТУРА
1. Л. Д. Ландау, А. И. Ахнезер, И. М. Лифшиц, «Курс общей физики» «Механика и молекулярная физика», «Наука», М. 1969 г. Гл. 8, стр. 77 – 88 2. И. В. Савельев «Курс общей физики» т. 1 «Наука», М. 1973 г. стр. 135 – 145 3. А. И. Китайгородский «Введение в физику», «Наука», М. 1973 г. стр. 62 – 74
|




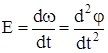 .
. и
и  для любой точки тела:
для любой точки тела: ;
;  ;
;  ;
; и
и 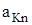 – ее тангенциальное и нормальное ускорения,
– ее тангенциальное и нормальное ускорения, ,
,  . (2)
. (2) . (3)
. (3) . (4)
. (4) . (5)
. (5) . (6)
. (6) . (6)
. (6) .
. . Причем
. Причем  , так как не учитывается масса блока В. Из уравнения (4) запишем
, так как не учитывается масса блока В. Из уравнения (4) запишем  , где r – радиус шкива. Очевидно, что
, где r – радиус шкива. Очевидно, что 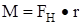 .
.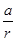 , где r – радиус шкива.
, где r – радиус шкива. , сек.
, сек. и т. д. (8)
и т. д. (8) (9)
(9)