 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Мин.значение .. Макс.значение
В диапазон входят все значения от минимального до максимального включительно. Пр. По номеру месяца m определить число дней d в нем. case m of 1,3,5,7..8,10,12: d:=31; 2: d:=28; 4,6,9,11: d:=30; end; Пр. По символу c определить и вывести, к какому классу символов он относится. case c of 'A'..'Z','a'..'z': writeln ('Лат.буква'); 'А'..'Я','а'..'п','р'..'я': writeln ('Рус.буква'); '0'..'9': writeln ('Цифра'); else writeln ('Другой символ'); end; Здесь отдельные диапазоны для русских букв от "а" до "п" и от "р" до "я" связаны с тем, что между "п" и "р" в кодовой таблице DOS находится ряд не-буквенных символов (см. Приложение 1). Если по ветви оператора case нужно выполнить несколько операторов, действует то же правило, что для оператора if (ветвь заключается в операторные скобки begin…end;). Примеры программ с условным оператором Приведем несколько примеров законченных программ, использующих РВП. Пр. Проверить, может ли быть построен прямоугольный треугольник по длинам сторон a,b,c. Проблема с решением этой задачи – не в проверке условия теоремы Пифагора, а в том, что в условии не сказано, какая из сторон может быть гипотенузой. Решений возможно несколько – запрашивать у пользователя ввод данных по возрастанию длины сторон, проверять все три возможных условия теоремы Пифагора и т.п. Используем наиболее естественное решение – перед проверкой условия теоремы Пифагора упорядочим величины a,b,c так, чтобы выполнялись соотношения a≤b≤c. Для этого используем прием с обменом значений переменных из главы 4. var a,b,c, { Длины сторон } s:real; { Буферная переменная для обмена } begin { СЕКЦИЯ ВВОДА ДАННЫХ } writeln; write ('Введите длину 1 стороны (больше 0):'); readln (a); write ('Введите длину 2 стороны (больше 0):'); readln (b); write ('Введите длину 3 стороны (больше 0):'); readln (c); { ДЕЛАЕМ СТОРОНУ a МИНИМАЛЬНОЙ, А СТОРОНУ c - МАКСИМАЛЬНОЙ } if (a>b) then begin s:=a; a:=b; b:=s; end; if (a>c) then begin s:=a; a:=c; c:=s; end; if (b>c) then begin s:=b; b:=c; c:=s; end; { ПРОВЕРЯЕМ УСЛОВИЕ ТЕОРЕМЫ ПИФАГОРА И ДЕЛАЕМ ВЫВОД } if abs(a*a+b*b-c*c)<1e-8 then writeln ('Прямоугольный треугольник может быть построен!') else writeln ('Прямоугольный треугольник не может быть построен!') end.
Пр. Определить, попадает ли точка плоскости, заданная координатами (a,b) в прямоугольник, заданный координатами двух углов (x1,y1) и (x2,y2). Как и в предыдущей задаче, было бы не совсем корректно требовать от пользователя вводить данные в определенном порядке – гораздо лучше при необходимости поменять x- и y-координаты прямоугольника так, чтобы пара переменных (x1,y1) содержала координаты левого нижнего угла прямоугольника, а (x2,y2) – правого верхнего. var x1,y1,x2,y2,a,b:real; begin writeln ('Введите координаты первого угла:'); read (x1,y1); writeln ('Введите координаты второго угла:'); read (x2,y2); if x1>x2 then begin a:=x1; x1:=x2; x2:=a; end; if y1>y2 then begin a:=y1; y1:=y2; y2:=a; end; writeln ('Введите координаты точки:'); read (a,b); if (x1<=a) and (a<=x2) and (y1<=b) and (b<=y2) then writeln ('Точка попадает в прямоугольник') else writeln ('Точка НЕ попадает в прямоугольник'); end.
Пр. Вводится денежная сумма в рублях и копейках. Программа печатает введенную сумму с правильной формой слов "рубли" и "копейки", например, "123 рубля 15 копеек". Окончание, используемое для слов "рубли" и "копейки", зависит от последней цифры суммы, которую можно получить, взяв остаток от деления на 10 (1058 рублей, 38 рублей и т.д.). Исключения – суммы с последними двумя цифрами от 11 до 19 включительно, которые всегда произносятся "рублей" и "копеек" (511 рублей, но 51 рубль). Используя эту информацию, составим программу. var r,k,o10,o100:integer; begin writeln; write ('Введите количество рублей, затем пробел и количество копеек:'); read (r,k); writeln; o10:=r mod 10; {Взяли последнюю цифру} o100:=r mod 100; {...и 2 последних цифры} write ('Правильно сказать: ',r,' '); {Печатаем число рублей, затем пробел} if (o100>10) and (o100<20) or (o10>4) or (o10=0) then write ('рублей') else if (o10>1) and (o10<5) then write ('рубля') else write ('рубль'); {аналогично для копеек:} o10:=k mod 10; o100:=k mod 100; write (' ',k,' '); {печатаем число копеек с пробелом до и после} if (o100>10) and (o100<20) or (o10>4) or (o10=0) then write ('копеек') else if (o10>1) and (o10<5) then write ('копейки') else write ('копейка'); end. Примеры составления алгоритмов заданий и использования в реализованных программах операторов ввода-вывода Задача 1 Даны два числа a и b. Получите число maxab, равное наибольшему из исходных. Если исходные числа равны, то maxab положить равным любому из них.
Решение Для решения задачи нужно ввести значения переменных a и b, сравнить их значения и в зависимости от результата сравнения maxab положить равным а или b. Обратите внимание на то, что вместе с результатом выводятся и исходные данные. Это позволит упростить тестирование и повысить наглядность вывода. Во втором варианте решения данной задачи мы не сравнивая присваиваем переменной-результату maxab первое «попавшееся» значение, а затем сравниваем это значение со вторым числом. Схема алгоритма
Рис. 1.1 Схема алгоритма программы задачи 1 (вариант 1)
Рис. 1.2 Схема алгоритма программы задачи 1 (вариант 2)
Текст программы
program lr1_1_1; { Даны два числа a и b. Получите число maxab, равное наибольшему из исходных. Если исходные числа равны, то maxab положить равным любому из них. Разработал учащий гр. ЭВС-31 Иванов И.И.} uses crt; var a,b,maxab:real; begin clrscr; write(‘Введите два числа через пробел ’); readln(a,b); if a>=b then maxab:=a else maxab:=b; writeln(‘ a= ’,a:8:2,’ b= ‘b:8:2,’ maxab= ‘,maxab:8:2); readkey; end.
Основная часть программы, соответствующая второй схеме будет выглядеть так.
maxab:=a; if maxab<b then maxab:=b;
С точки зрения времени выполнения программы первый вариант предпочтителен, но на практике приходится пользоваться обоими. Например, если необходимо найти наибольший из трех, то какой бы вариант не был применен для нахождения наибольшего из первых двух, этот наибольший нужно сравнить с третьим, т.е. возникнет необходимость во втором варианте.
Контрольные примеры
Контрольный пример 1 Исходные данные: a=1, b=2; результат maxab=2. Контрольный пример 2 Исходные данные: a=3, b=1; результат maxab=3. Контрольный пример 3 Исходные данные: a=1, b=1; результат maxab=1.
Примечание. При записи результата мы не учитываем формат вывода его в программе.
Содержание пояснительной записки 1. Текст задания; 2. Описание алгоритма решения задачи (в виде блок-схемы) 3. Описание входных и выходных данных программы ( в виде таблицы и в программе) 4. Вклеенный машинный листинг программы на языке pascal. 5. Выводы по работе Варианты 1) 2*c - d + ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾
3) -2*c + d*82 4) lg(2*c) + d - 52 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾
5) arctg(c/4) - d*62 6) -2*c - ln(d) + 53 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ a*a - 1
7) 2*c - lg(d/4) 8) tg ( c ) - d*23 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ a*a - 1 2*a - 1
9) 2*c - d/23 10) 4*c + d - 1 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ ln(1 -
11) 2*c - d* ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ c + a - 1 d + a*a - 1
13) arctg(c - d/2) 14) 4*lg ( c ) - d/2 + 23 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 2*a - 1 a*a - 1
15) c*tg(b + 23) 16) c/d + ln(3*a/2) ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ a/2 -4*d - 1 c - a + 1 17) 2*c + lg(d)*51 18) 2*c + ln(d/4) + 23 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ d - a - 1 a*a - 1
19) 42*c - d/2 + 1 20) arctg(2*c)/d + 2 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ a*a - ln(b-5) d - a*a - 1
21) arctg(12/c) + 73 22) 2*c/a - d*d ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ a*a - 1 d + tg(a - 1)
23) ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 1 + a*b b*a -1
25) -25/a + c - tg(b) 26) lg(4*a - 1) + b/2 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 1 + c*b/2 b*c - 5
27) 8*lg(b + 1) - c 28) 4*a - ln(b - 1) ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ a/2 + b*c c + 18
29) arctg(4*b)/c - 1 30) arctg(b) + c*b - a/4 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 12*c + a - b a*b - 1
31) a + ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 4*b*a + 1 2*a*c - 1
33) 2*b - ln(a + b)*c 34) 41 - d/4 - 1 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ c/4 - 1 c/tg(b + a) - d
35) a - b*4 - 1 36) lg(b/a + 4)*c ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ c/31 + tg(a*b) 41*c - b + 1
37) lg(21 - a)*c/4 38) c - ln(33 + b)/4 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 1 + c/a + b a*c/b - 1
39) 2*b - 38*c 40) arctg(c/4 + 28)*d ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ arctg(b + a)/c + 1 a/d - c - 1
41) a*b/4 - 1 42) 1 + a - b/2 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾
43) ln(a*b + 2)*c 44) lg(4*b - c)*a ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 41 - b/c + 1 b + c/28 - 1
45) 2*c + tg(a - 21) 46) 4/c + tg(3*a) ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ c/a*b + 1 c/a - b - 1
47) 8*lg(b - 1) - c 48) 4*ln(a/b) + 1 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ a*2 + b/c c*b - 18 + a
49) 4*ln(b)/c + 1 50) arctg(b - c)/b + a/4 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 2*c + a*c - b a*b - 1
51) arctg(a - c)*b + 28 52) c*b - 24 + a ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ 4*b/a + 1 b/lg(2*c - 1) + a
53) ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ a - c/4 + 1 a - c/b + a*d
55) a + tg(b/4 - 1) 56) b*a + c/2 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ c/3 - a*b 4*c - tg(b + 1)
57) lg(25 + 2*a/c) 58) c + 23 - b*4 ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ c*a - b - 1 a - ln(a + c/b - 1)
59) b/2 - 53/c 60) c*4 + 28/d ¾¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾ arctg(b - a)*c + 1 5 - arctg(a*d - c - 1)
Контрольныe вопросы 1. Перечислите команды ввода языка Паскаль, опишите их формат, особенности использования 2. Перечислите команды вывода языка Паскаль, опишите их формат, особенности использования 3. Перечислите типы данных, используемые в языке Паскаль, дайте им краткую характеристику |





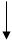





 Да
Да


 Нет
Нет

 2) c + 4*d -
2) c + 4*d - 
 - 1 1 -
- 1 1 - 
 tg(
tg(  12)
12)  - d + 2
- d + 2 + d -4*a 24)
+ d -4*a 24)  + b -
+ b -  -
-  32)
32)  + a
+ a - b*a + c b*
- b*a + c b*  - a + b/c 54)
- a + b/c 54)  + 1
+ 1