 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Завдання на лабораторну роботу. 12
2.1 Побудова кодеру і дослідження процесу кодування. Дослідити процес кодування двійкового повідомлення завадостійким циклічним кодом. Представити свої ініціали у двійковому коді, наприклад, у міжнародному телеграфному коді МТК-2, приписавши у старшому розряді 0 при розташуванні літери на регістрі кирилиці або 1 при розташуванні літери на регістрі чисел та символів, (або у коді Бодо; у коді АSKII, тощо), після чого: а) визначити відстані Хемінга між кодовими комбінаціями першої та другої, другої та третьої, першої та третьої літер; б) закодувати кожну із літер завадостійким циклічним кодом, який задається кодоутворюючим поліномом, визначеним викладачем із переліку у Додатку 1. При цьому необхідно: - отримати залишки шляхом ділення інформаційних складових на утворюючий поліном; - сформувати кодові слова, якими повинні бути представлені літери ініціалів при передачі їх в каналі зв’язку; в) визначити кодову відстань між представленими у циклічному коді літерами ініціалів; г) у відповідності з кодоутворюючим поліномом розробити функціональну схему кодуючого пристрою; д) відобразити процес отримання залишку (у вигляді двійкової послідовності) шляхом покрокового заповнення таблиці стану тригерів регістру кодуючого пристрою (для кожної літери); 2.2 Побудова декодеру і дослідження процесу декодування. Дослідити процес декодування повідомлення, закодованого завадостійким циклічним кодом: а) перевірити правильність сформованих кодових слів (приналежності їх до категорії дозволених кодових комбінацій) шляхом ділення їх на утворюючий поліном (залишки повинні дорівнювати нулю); б) перевірити здатність коду виявити помилки певної кратності, для чого: - ввести помилки у вигляді багаточлена помилки Е(х), взятого за завданням викладача із переліку у Додатку 1, додавши його до багаточленів сформованих у результаті кодування у пункті 2.2, кодових слів першої, другої та третьої літер; - поділити поліноми отриманих спотворених кодових комбінацій на утворюючий поліном і проаналізувати отримані синдроми (залишки); в) визначити надлишковість та відносну швидкість коду; г) визначити, чи може код забезпечити виявлення помилок кратності 2 та 3; д) відобразити процес отримання синдрому (залишку) при декодуванні у відсутності помилок шляхом покрокового заповнення таблиці стану тригерів регістру декодуючого пристрою для кожної літери; е) відобразити процес отримання синдрому при декодуванні спотворених кодових слів першої, другої та третьої літер шляхом покрокового заповнення таблиці стану тригерів регістру декодуючого пристрою. Порівняти та проаналізувати результати, отримані вище.
3. Приклад виконання. Іваненко Петро Семенович Ініціали ІПС можна закодувати з використанням того чи іншого двійкового коду відповідних літер. Наприклад, за номером літери у алфавіті (без урахування ґ та пробілу). Літера І - 10, П - 19, С - 21. У двійковому п’ятизначному коді коди літер відповідно будуть такими: І - 01010, П - 10011, С - 10101. а) Відстані Хемінга:
Математична модель кодування циклічним кодом.
б) Кодування циклічним кодом з поліномом Р(х)= х3+х+1.
Кодуємо літеру
отримуємо залишок діленням
x6+x4+x3! x3+1 0 0 x3
x+1=RI(x)
Кодове слово завадостійкого циклічного коду буде мати вигляд
Таким же чином отримують
Математична модель декодування циклічного коду.
Перевірка вірності формування x6+x4+x+1 !x3+x+1
0 0 x3+x+1
0 0 0 Залишок дорівнює нулю. Перевірочні розряди отримані вірно. Аналогічно перевіряють в) Визначення г) Перевіряємо можливість виявлення помилок. Нехай багаточлен помилки Е(х)=х5+1(кратність помилки 2) Спотворене кодове слово буде
ділимо
x6 + x5 + x4 + x !x3+x+1
0 + x5 + x3+ x
0 0 x2 +x - залишок не дорівнює нулю. Помилка виявлена. д)Надлишковість коду 3/8; відносна швидкість 5/8. є) Для визначення можливостей коду щодо виявлення помилок кратності 2 і 3 необхідно встановити відповідність наявної кількості перевірочних розрядів вимогам з виявлення помилок заданої кратності скориставшись верхнею межею Хемінга.
12 |





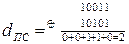
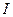
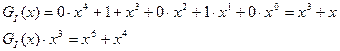
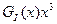 на P(x).
на P(x). x6+x4 !x3+x+1
x6+x4 !x3+x+1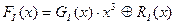 .
. . Враховуючи, що його розрядність п повинна дорівнювати 8 (п’ять інформаційних розрядів і три перевірочні), то у двійковому коді це буде
. Враховуючи, що його розрядність п повинна дорівнювати 8 (п’ять інформаційних розрядів і три перевірочні), то у двійковому коді це буде 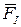 =01010011.
=01010011. .
. декодуванням. Ділимо
декодуванням. Ділимо 
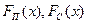
 аналогічно пункту а).
аналогічно пункту а).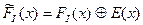
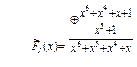
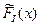 на
на