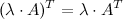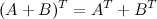ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Источники: http://edu.dvgups.ru/METDOC/ENF/VMATEM/WM/METOD/SYASINA/WEBUMK/frame/1_1_2.htm
ЛАБОРАТОРНАЯ РАБОТА №10
ИСПОЛЬЗОВАНИЕ ДВУМЕРНЫХ МАССИВОВ ПРИ РАБОТЕ С КЛАССАМИ
Цель занятия: 1.Получение практических навыков в работе с двумерными массивами. 2.Получение навыков в организации ввода/вывода значений переменных регулярных типов данных.
ВОПРОСЫ ДЛЯ КОНТРОЛЯ 1. Что понимается под массивом? 2. Как обозначаются в программе элементы двумерного массива? 3. Форма записи двумерного массива? 4. Обращение к элементам двумерного массива? 5. Как создается в программе двумерный массив? 6. Как организуется в программе ввод двумерного массива? 7. Как организуется в программе вывод двумерный массива? 8. Как хранятся в памяти элементы двумерного массива? 9. Как производится обращение к элементам двумерного массива? 10. Как организовывается индексация двумерного массива?
ПОСТАНОВКА ЗАДАНИЯ 1. Выполнить задание по вариантам, указанным преподавателем (таблица 10.1.).
СОДЕРЖАНИЕ ОТЧЕТА 1.Постановка задачи. 2.Текст программы. 3.Таблица данных и результатов.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Включить ПК.
2.Загрузить систему Microsoft Visual Studio C#
3.Выполнить задание по вариантам, указанным преподавателем (таблица 10.1.). Примечание: При составлении программы руководствоваться методическими указаниями и примером составления программы.
4.Ввести по мере выполнения программы исходные данные. Результаты занести в отчет.
5.Закончить работу с системой Microsoft Visual Studio C# без сохранения программы.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ДВУМЕРНЫЙ МАССИВ Действия над матрицами Сложение матриц Определение. Суммой матриц A и B одинаковой размерности называют матрицу C=A+B того же размера, элементы которой Сумма матриц разной размерности не определяется. Пусть
Пример. Даны матрицы
Решение. По определению суммы матриц, матрица
Свойства сложения: 1. 2. 3.
Умножение матрицы на число Определение. Произведением матрицы
Размер матрицы Свойства произведения матрицы на число: 1. 2. 3. 4. 5. Пример. Даны матрицы Найти матрицу
Решение.
Умножение матриц Определение. Произведением матрицы
Из формулы следует, что матрицу Правило умножения матриц еще называют правилом «строка на столбец», так как по формуле элемент
Свойства произведения матриц: 1. 2. 3. 4. 5. 6. Замечание. Произведение матриц зависит от порядка множителей, поэтому не всегда Рассмотрим примеры умножения матриц. Пример. Вычислить произведение матриц
Решение. Поскольку матрицы
Пример. Вычислить произведение матриц
Решение. Произведение матриц
Произведение Пример. Вычислить произведение матриц
Решение. Размеры данных матриц Разность матриц Разность двух матриц одинакового размера можно определить через операцию сложения матриц и через умножение матрицы на число. Вычитание матриц вводится следующим образом: То есть к матрице Разностью матриц На практике же от элементов матрицы Вычитать можно только матрицы одинакового размера. Пример Задание. Найти матрицу Решение.
Ответ.
Транспонирование матрицы Транспонирование матрицы – это операция над матрицей, когда ее строки становятся столбцами с теми же номерами. Пример. Задание. Найти матрицу Решение. Ответ. Если матрица Свойства операции транспонирования матриц: 1. 2. 3. 4.
Источники: http://edu.dvgups.ru/METDOC/ENF/VMATEM/WM/METOD/SYASINA/WEBUMK/frame/1_1_2.htm |



 равны суммам соответствующих элементов матрицA иB :
равны суммам соответствующих элементов матрицA иB :  .
. и
и 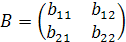 , тогда
, тогда .
. и
и  . Найти матрицу
. Найти матрицу  .
.
 .
. (коммутативный закон);
(коммутативный закон); (ассоциативный закон);
(ассоциативный закон); , где
, где  – нулевая матрица.
– нулевая матрица. на число называют матрицу, элементы которой получены умножением каждого элемента матрицы А на число:
на число называют матрицу, элементы которой получены умножением каждого элемента матрицы А на число: .
. одинаков.
одинаков. .
. .
.
 .
. где
где  – нулевая матрица.
– нулевая матрица.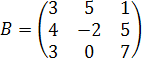 .
. .
.
 .
. на матрицу
на матрицу  называют матрицу
называют матрицу  , элементы которой
, элементы которой  определяются формулами:
определяются формулами:
 произведения равен сумме парных произведений элементов i-й строки матрицы
произведения равен сумме парных произведений элементов i-й строки матрицы 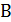 . Таким образом, умножать матрицы
. Таким образом, умножать матрицы 
 .
. .
. .
. .
. .
. .
. .
. . Если для произведения матриц выполняется
. Если для произведения матриц выполняется  , то матрицы
, то матрицы  и
и  называются перестановочными.
называются перестановочными. и
и  имеет смысл. Получаем в произведении матрицу
имеет смысл. Получаем в произведении матрицу  :
:

 .
.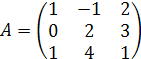 и
и  .
. :
: .
. не имеет смысла так как число столбцов матрицы
не имеет смысла так как число столбцов матрицы  и
и  .
. и
и  , следовательно, произведение этих матриц определено, размер матрицы произведения
, следовательно, произведение этих матриц определено, размер матрицы произведения  . Имеем
. Имеем  .
.
 прибавляется матрица
прибавляется матрица  , умноженная на (-1).
, умноженная на (-1). такого же размера, получаемая из исходных путем прибавления к матрице
такого же размера, получаемая из исходных путем прибавления к матрице  , если
, если 



 , если
, если 


 , то матрица
, то матрица  .
.