 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Метод Рунге-Кутта IV порядка
Лабораторная работа № Численное решение задачи Коши для обыкновенных дифференциальных уравнений Выполнить только для методов Рунге-Кутта 3 и 4 порядков !!! 11.1 Постановка задачи Цель: освоить алгоритмы методов решения задачи Коши для ОДУ. Задание: 1. Найти численное решение задачи Коши 

методами Эйлера, предиктор-корректор, Рунге-Кутта 3 и 4 порядков на сетках с шагом τ = 0,1; τ = 0,05; τ = 0,025, соответственно, согласно выбранному варианту. 2. На последовательности указанных сеток проверить сходимость полученного решения для указанных методов. 3. Для сопоставления методов вычислить  , где , где 
 - точное решение - точное решение
| вариант | f(t,u) | t0 | T | u0 | точное решение | |  | 0,1 | 1,1 | 0,3314113 |  | |  | | 0,9 | -1 |  | |  | | 0,9 | |  | |  | | 0,9 | |  | |  | | 0,9 | |  | |  | | 0,9 | 3,4 |  | |  | | 0,9 | |  |
Ход работы Решим задачу Коши для дифференциального уравнения 
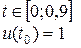
/Точное решение  Метод Эйлера Вычислительный процесс строится по формуле  . (1) . (1)
Применяя (1) к нашему уравнению получаем расчетную формулу: 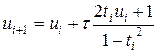 , ,
t0=0 и u0=1 - начальные условия. На сетке с шагом τ = 0,1 получим для t1=0,1 
для t2=0,2  результаты дальнейших вычислений поместим в таблицу 11.1 Аналогичные действия выполняются на сетках с шагами τ = 0,05 и τ = 0,025, результаты вычислений приведены в таблицах 11.2, 11.3, соответственно. Метод предиктор-корректор Вычислительный процесс строится по формулам 1 шаг  (2) (2) 2 шаг  . . Применяя (2) к нашему уравнению получаем расчетные формулы: 1 шаг  2 шаг  , , t0=0 и u0=1 - начальные условия, а  . . При τ = 0,1 для t1=0,1 на первом шаге получим 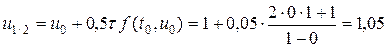
на втором шаге получим 
для t2=0,2 на первом шаге получим 
на втором шаге получим 
результаты дальнейших вычислений поместим в таблицу 11.1 Аналогичные действия выполняются на сетках с шагами τ = 0,05 и τ = 0,025, результаты вычислений приведены в таблицах 11.2, 11.3, соответственно. Методы Рунге-Кутта Метод Рунге-Кутта III порядка Метод Рунге-Кутта III порядка точности можно выполнить по следующим формулам:  (3) (3)  (4) (4)
Проведем вычисления, используя формулы (3), которые применительно к нашему уравнению примут вид: 
При τ = 0,1 для t1=0,1 получим 
для следующей точки сетки t1=0,2 получим 
результаты дальнейших вычислений поместим в таблицу 11.1 Аналогичные действия выполняются на сетках с шагами τ = 0,05 и τ = 0,025, результаты вычислений приведены в таблицах 11.2, 11.3, соответственно. Метод Рунге-Кутта IV порядка Метод Рунге-Кутта IV порядка точности можно выполнить по следующим формулам:  (5) (5)  (6) (6)
Проведем вычисления, используя формулы (5), которые применительно к нашему уравнению примут вид: 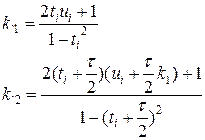

При τ = 0,1 для t1=0,1 получим 
для следующей точки сетки t1=0,2 получим 
результаты дальнейших вычислений поместим в таблицу 11.1 Аналогичные действия выполняются на сетках с шагами τ = 0,05 и τ = 0,025, результаты вычислений приведены в таблицах 11.2, 11.3, соответственно Таблица 11.1 τ = 0,1 | i | ti | ui(1) | | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | Точное решение | | | | | | | | | 0,1 | 1,1 | 1,1107769 | 1,1111293 | 1,1111112 | 1,1111111 | | 0,2 | 1,2232323 | 1,2490634 | 1,2500445 | 1,2500003 | 1,2500000 | | 0,3 | 1,3783670 | 1,4265125 | 1,4286573 | 1,4285723 | 1,4285714 | | 0,4 | 1,5791385 | 1,662403 | 1,6668231 | 1,6666689 | 1,6666667 | | 0,5 | 1,8485802 | 1,9910526 | 2,0002894 | 2,0000057 | 2,0000000 | | 0,6 | 2,2283909 | 2,47987 | 2,5005744 | 2,500016 | 2,5000000 | | 0,7 | 2,8024642 | 3,2811908 | 3,3346467 | 3,3333868 | 3,3333333 | | 0,8 | 3,7678465 | 4,8227644 | 5,0039483 | 5,0002546 | 5,0000000 | | 0,9 | 5,7202228 | 8,8792486 | 10,022309 | 10,0027518 | 10,000000 |
Таблица 11.2 τ = 0,05 | i | ti | ui(2) | | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | Точное решение | | | | | | | | | 0,05 | 1,0500000 | 1,052595372 | 1,0526327 | 1,05263158 | 1,0526316 | | 0,10 | 1,1053885 | 1,111026267 | 1,1111135 | 1,111111115 | 1,1111111 | | 0,15 | 1,1670591 | 1,176320108 | 1,1764745 | 1,176470597 | 1,1764706 | | 0,20 | 1,2361188 | 1,249760333 | 1,2500058 | 1,250000017 | 1,2500000 | | 0,25 | 1,3139546 | 1,332971349 | 1,3333415 | 1,333333364 | 1,3333333 | | 0,30 | 1,4023267 | 1,428039694 | 1,4285827 | 1,428571481 | 1,4285714 | | 0,35 | 1,5035023 | 1,537690756 | 1,5384769 | 1,538461626 | 1,5384615 | | 0,40 | 1,6204511 | 1,665553169 | 1,6666875 | 1,66666681 | 1,6666667 | | 0,45 | 1,7571393 | 1,816566163 | 1,8182101 | 1,818182052 | 1,8181818 | | 0,50 | 1,9189841 | 1,997628759 | 2,0000389 | 2,000000384 | 2,0000000 | | 0,55 | 2,1135831 | 2,218676366 | 2,2222767 | 2,222222865 | 2,2222222 | | 0,60 | 2,3519301 | 2,494552545 | 2,5000784 | 2,50000111 | 2,5000000 | | 0,65 | 2,6505486 | 2,848454822 | 2,8572600 | 2,857144864 | 2,8571429 | | 0,70 | 3,0354588 | 3,318743148 | 3,3335177 | 3,333337208 | 3,3333333 | | 0,75 | 3,5501296 | 3,973657875 | 4,0003118 | 4,000008219 | 4,0000000 | | 0,80 | 4,273009 | 4,947137683 | 5,0005861 | 5,000020041 | 5,0000000 | | 0,85 | 5,3614554 | 6,541554239 | 6,667967 | 6,666727534 | 6,6666667 | | 0,9 | 7,1838832 | 9,604729062 | 10,0038618 | 10,000272049 | | Таблица 11.3 τ = 0,025 | i | ti | ui(3) | | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | Точное решение | | | | | | | | | 0,025 | 1,025 | 1,025636818 | 1,025641092 | 1,025641026 | 1,025641026 | | 0,05 | 1,051297686 | 1,052622491 | 1,052631717 | 1,052631579 | 1,052631579 | | 0,075 | 1,078995174 | 1,081066327 | 1,081081297 | 1,081081081 | 1,081081081 | | 0,1 | 1,108205715 | 1,111089775 | 1,111111413 | 1,111111111 | 1,111111111 | | 0,125 | 1,139055239 | 1,142828149 | 1,142857539 | 1,142857143 | 1,142857143 | | 0,15 | 1,171684161 | 1,176432672 | 1,176471089 | 1,176470589 | 1,176470588 | | 0,175 | 1,206249513 | 1,212072881 | 1,212121829 | 1,212121213 | 1,212121212 | | 0,2 | 1,242927458 | 1,249939487 | 1,250000746 | 1,250000001 | 1,25 | | 0,225 | 1,281916286 | 1,290247781 | 1,290323472 | 1,290322582 | 1,290322581 | | 0,25 | 1,323439981 | 1,333241735 | 1,333334388 | 1,333333335 | 1,333333333 | | 0,275 | 1,367752514 | 1,379198929 | 1,379311585 | 1,379310347 | 1,379310345 | | 0,3 | 1,415143018 | 1,428436554 | 1,42857288 | 1,428571432 | 1,428571429 | | 0,325 | 1,465942079 | 1,48131873 | 1,481483175 | 1,481481486 | 1,481481481 | | 0,35 | 1,520529426 | 1,538265516 | 1,538463511 | 1,538461544 | 1,538461538 | | 0,375 | 1,579343403 | 1,599764082 | 1,600002297 | 1,600000007 | 1,6 | | 0,4 | 1,642892714 | 1,666382656 | 1,666669342 | 1,666666676 | 1,666666667 | | 0,425 | 1,711771112 | 1,738788116 | 1,739133555 | 1,739130447 | 1,739130435 | | 0,45 | 1,786675931 | 1,817768352 | 1,818185465 | 1,818181834 | 1,818181818 | | 0,475 | 1,868431678 | 1,904261009 | 1,90476618 | 1,904761925 | 1,904761905 | | 0,5 | 1,958020382 | 1,99939082 | 2,000005031 | 2,000000026 | | | 0,525 | 2,056621061 | 2,104518692 | 2,105269107 | 2,105263191 | 2,105263158 | | 0,55 | 2,165661686 | 2,221307086 | 2,222229299 | 2,222222265 | 2,222222222 | | 0,575 | 2,286888491 | 2,351808375 | 2,352949653 | 2,352941232 | 2,352941176 | | 0,6 | 2,422459799 | 2,49858618 | 2,500010236 | 2,500000073 | 2,5 | | 0,625 | 2,575075102 | 2,664884979 | 2,666679147 | 2,666666765 | 2,666666667 | | 0,65 | 2,748155877 | 2,854871963 | 2,857158246 | 2,857142991 | 2,857142857 | | 0,675 | 2,946104043 | 3,073989747 | 3,076942306 | 3,076923262 | 3,076923077 | | 0,7 | 3,174679954 | 3,329484041 | 3,33335774 | 3,333333594 | 3,333333333 | | 0,725 | 3,441569754 | 3,631216479 | 3,636395199 | 3,636364013 | 3,636363636 | | 0,75 | 3,757262832 | 3,992959864 | 4,000041746 | 4,00000056 | | | 0,775 | 4,136456789 | 4,434545749 | 4,444501197 | 4,444445309 | 4,444444444 | | 0,8 | 4,600400953 | 4,985597471 | 5,000079829 | 5,000001396 | | | 0,825 | 5,181001059 | 5,69240083 | 5,714402972 | 5,714288103 | 5,714285714 | | 0,85 | 5,928449336 | 6,631475875 | 6,666848923 | 6,666671074 | 6,666666667 | | 0,875 | 6,926500136 | 7,938905352 | 8,000305882 | 8,000009011 | | | 0,9 | 8,326113494 | 9,881679234 | 10,000572906 | 10,000021333 | | Проверка сходимости полученного решения для указанных методов. Для проверки сходимости методов Эйлера, предиктор-корректор, Рунге-Кутта вычислим максимальную разность между соответствующими значениями функции на сетках ui(1), ui(2), ui(3), т.е. maxi /u2i(2)- ui(1)/, maxi /u2i(3)- ui(2)/. Результаты вычислений приведены в таблицах 11.4, 11.5. Таблица 11.4 | i | ti | /u2i(2)- ui(1)/ | | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | | | | | | | | 0,1 | 0,0053885 | 0,000249367 | 1,58E-05 | 8,5E-08 | | 0,2 | 0,0128865 | 0,000696933 | 3,87E-05 | 2,83E-07 | | 0,3 | 0,0239597 | 0,001527194 | 7,46E-05 | 8,19E-07 | | 0,4 | 0,0413126 | 0,003150169 | 0,0001356 | 2,09E-06 | | 0,5 | 0,0704039 | 0,006576159 | 0,0002505 | 5,316E-06 | | 0,6 | 0,1235392 | 0,014682545 | 0,000496 | 1,489E-05 | | 0,7 | 0,2329946 | 0,037552348 | 0,001129 | 4,9592E-05 | | 0,8 | 0,5051625 | 0,124373283 | 0,0033622 | 0,000234559 | | 0,9 | 1,4636604 | 0,725480462 | 0,0184472 | 0,002479751 | | maxi | 1,4636604 | 0,725480462 | 0,0184472 | 0,002479751 | Таблица 11.5 | i | ti | /u2i(3)- ui(2)/ | | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | | | | | | | | 0,05 | 0,001297686 | 2,7119E-05 | 9,83E-07 | 1E-09 | | 0,10 | 0,002817215 | 6,3508E-05 | 2,087E-06 | 4E-09 | | 0,15 | 0,004625061 | 0,000112564 | 3,411E-06 | 8E-09 | | 0,20 | 0,006808658 | 0,000179154 | 5,054E-06 | 1,6E-08 | | 0,25 | 0,009485381 | 0,000270386 | 7,112E-06 | 2,9E-08 | | 0,30 | 0,012816318 | 0,00039686 | 9,82E-06 | 4,9E-08 | | 0,35 | 0,017027126 | 0,00057476 | 1,3389E-05 | 8,2E-08 | | 0,40 | 0,022441614 | 0,000829487 | 1,8158E-05 | 1,34E-07 | | 0,45 | 0,029536631 | 0,001202189 | 2,4635E-05 | 2,18E-07 | | 0,50 | 0,039036282 | 0,001762061 | 3,3869E-05 | 3,58E-07 | | 0,55 | 0,052078586 | 0,00263072 | 4,7401E-05 | 6E-07 | | 0,60 | 0,070529699 | 0,004033635 | 6,8164E-05 | 1,037E-06 | | 0,65 | 0,097607277 | 0,006417141 | 0,000101754 | 1,873E-06 | | 0,70 | 0,139221154 | 0,010740893 | 0,00015996 | 3,614E-06 | | 0,75 | 0,207133232 | 0,019301989 | 0,000270054 | 7,659E-06 | | 0,80 | 0,327391953 | 0,038459788 | 0,000506271 | 1,8645E-05 | | 0,85 | 0,566993936 | 0,089921636 | 0,001118077 | 5,646E-05 | | 0,9 | 1,142230294 | 0,276950172 | 0,003288894 | 0,000250716 | | maxi | 1,142230294 | 0,276950172 | 0,003288894 | 0,000250716 | Полученные данные о максимальных разностях внесем в отдельную таблицу 11.6. Таблица 11.6 | maxi /u2i(k)- ui(k-1)/ | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | | maxi /u2i(2)- ui(1)/ | 1,4636604 | 0,725480462 | 0,0184472 | 0,002479751 | | maxi /u2i(3)- ui(2)/ | 1,142230294 | 0,276950172 | 0,003288894 | 0,000250716 | Из таблицы 11.6 видно, что рассматриваемая нами величина maxi /u2i(k)- ui(k-1)/для каждого метода уменьшается, а это характерно для сходящегося процесса. Сопоставление методов Для сопоставления методов необходимо вычислить  , где , где 
 - точное решение - точное решение
Используя данные таблиц 11.1, 11.2, 11.3 вычислим  , результаты представим в таблицах 11.7, 11.8, 11.9. , результаты представим в таблицах 11.7, 11.8, 11.9.
Таблица 11.7 τ = 0,1 | i | ti |  | | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | | | | | | | | 0,1 | 0,0111111 | 0,0003342 | 1,82E-05 | 1E-07 | | 0,2 | 0,0267677 | 0,0009366 | 4,45E-05 | 3E-07 | | 0,3 | 0,0502044 | 0,0020589 | 8,59E-05 | 9E-07 | | 0,4 | 0,0875282 | 0,0042637 | 0,0001564 | 2,2E-06 | | 0,5 | 0,1514198 | 0,0089474 | 0,0002894 | 5,7E-06 | | 0,6 | 0,2716091 | 0,02013 | 0,0005744 | 1,6E-05 | | 0,7 | 0,5308691 | 0,0521425 | 0,0013134 | 5,35E-05 | | 0,8 | 1,2321535 | 0,1772356 | 0,0039483 | 0,0002546 | | 0,9 | 4,2797772 | 1,1207514 | 0,022309 | 0,0027518 | | maxi | 4,2797772 | 1,1207514 | 0,022309 | 0,0027518 | Таблица 11.8 τ = 0,05 | i | ti |  | | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | | | | | | | | 0,05 | 0,0026316 | 3,6228E-05 | 1,1E-06 | 2E-08 | | 0,10 | 0,0057226 | 8,4833E-05 | 2,4E-06 | 1,5E-08 | | 0,15 | 0,0094115 | 0,000150492 | 3,9E-06 | 3E-09 | | 0,20 | 0,0138812 | 0,000239667 | 5,8E-06 | 1,7E-08 | | 0,25 | 0,0193787 | 0,000361951 | 8,2E-06 | 6,4E-08 | | 0,30 | 0,0262447 | 0,000531706 | 1,13E-05 | 8,1E-08 | | 0,35 | 0,0349592 | 0,000770744 | 1,54E-05 | 1,26E-07 | | 0,40 | 0,0462156 | 0,001113531 | 2,08E-05 | 1,1E-07 | | 0,45 | 0,0610425 | 0,001615637 | 2,83E-05 | 2,52E-07 | | 0,50 | 0,0810159 | 0,002371241 | 3,89E-05 | 3,84E-07 | | 0,55 | 0,1086391 | 0,003545834 | 5,45E-05 | 6,65E-07 | | 0,60 | 0,1480699 | 0,005447455 | 7,84E-05 | 1,11E-06 | | 0,65 | 0,2065943 | 0,008688078 | 0,0001171 | 1,964E-06 | | 0,70 | 0,2978745 | 0,014590152 | 0,0001844 | 3,908E-06 | | 0,75 | 0,4498704 | 0,026342125 | 0,0003118 | 8,219E-06 | | 0,80 | 0,726991 | 0,052862317 | 0,0005861 | 2,0041E-05 | | 0,85 | 1,3052113 | 0,125112461 | 0,0013003 | 6,0834E-05 | | 0,9 | 2,8161168 | 0,395270938 | 0,0038618 | 0,000272049 | | maxi | 2,8161168 | 0,395270938 | 0,0038618 | 0,000272049 | Таблица 11.3 τ = 0,025 | i | ti |  | | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка | | | | | | | | 0,025 | 0,000641026 | 4,208E-06 | 6,6E-08 | | | 0,05 | 0,001333893 | 9,088E-06 | 1,38E-07 | | | 0,075 | 0,002085907 | 1,4754E-05 | 2,16E-07 | | | 0,1 | 0,002905396 | 2,1336E-05 | 3,02E-07 | | | 0,125 | 0,003801904 | 2,8994E-05 | 3,96E-07 | | | 0,15 | 0,004786427 | 3,7916E-05 | 5,01E-07 | 1E-09 | | 0,175 | 0,005871699 | 4,8331E-05 | 6,17E-07 | 1E-09 | | 0,2 | 0,007072542 | 6,0513E-05 | 7,46E-07 | 1E-09 | | 0,225 | 0,008406295 | 7,48E-05 | 8,91E-07 | 1E-09 | | 0,25 | 0,009893352 | 9,1598E-05 | 1,055E-06 | 2E-09 | | 0,275 | 0,011557831 | 0,000111416 | 1,24E-06 | 2E-09 | | 0,3 | 0,013428411 | 0,000134875 | 1,451E-06 | 3E-09 | | 0,325 | 0,015539402 | 0,000162751 | 1,694E-06 | 5E-09 | | 0,35 | 0,017932112 | 0,000196022 | 1,973E-06 | 6E-09 | | 0,375 | 0,020656597 | 0,000235918 | 2,297E-06 | 7E-09 | | 0,4 | 0,023773953 | 0,000284011 | 2,675E-06 | 9E-09 | | 0,425 | 0,027359323 | 0,000342319 | 3,12E-06 | 1,2E-08 | | 0,45 | 0,031505887 | 0,000413466 | 3,647E-06 | 1,6E-08 | | 0,475 | 0,036330227 | 0,000500896 | 4,275E-06 | 2E-08 | | 0,5 | 0,041979618 | 0,00060918 | 5,031E-06 | 2,6E-08 | | 0,525 | 0,048642097 | 0,000744466 | 5,949E-06 | 3,3E-08 | | 0,55 | 0,056560536 | 0,000915136 | 7,077E-06 | 4,3E-08 | | 0,575 | 0,066052685 | 0,001132801 | 8,477E-06 | 5,6E-08 | | 0,6 | 0,077540201 | 0,00141382 | 1,0236E-05 | 7,3E-08 | | 0,625 | 0,091591565 | 0,001781688 | 1,248E-05 | 9,8E-08 | | 0,65 | 0,10898698 | 0,002270894 | 1,5389E-05 | 1,34E-07 | | 0,675 | 0,130819034 | 0,00293333 | 1,9229E-05 | 1,85E-07 | | 0,7 | 0,158653379 | 0,003849292 | 2,4407E-05 | 2,61E-07 | | 0,725 | 0,194793882 | 0,005147157 | 3,1563E-05 | 3,77E-07 | | 0,75 | 0,242737168 | 0,007040136 | 4,1746E-05 | 5,6E-07 | | 0,775 | 0,307987655 | 0,009898695 | 5,6753E-05 | 8,65E-07 | | 0,8 | 0,399599047 | 0,014402529 | 7,9829E-05 | 1,396E-06 | | 0,825 | 0,533284655 | 0,021884884 | 0,00011726 | 2,389E-06 | | 0,85 | 0,738217331 | 0,035190792 | 0,00018226 | 4,407E-06 | | 0,875 | 1,073499864 | 0,061094648 | 0,00030588 | 9,011E-06 | | 0,9 | 1,673886506 | 0,118320766 | 0,00057291 | 2,1333E-05 | | maxi | 1,673886506 | 0,118320766 | 0,00057291 | 2,1333E-05 | Полученные данные для  внесем в таблицу 11.6. внесем в таблицу 11.6. Таблица 11.6  | Метод Эйлера | Предиктор-корректор | Метод Рунге-Кутта III порядка | Метод Рунге-Кутта IV порядка |  τ = 0,1 τ = 0,1 | 4,2797772 | 1,1207514 | 0,022309 | 0,0027518 |  τ = 0,05 τ = 0,05 | 2,8161168 | 0,395270938 | 0,0038618 | 0,000272049 |  τ = 0,025 τ = 0,025 | 1,673886506 | 0,118320766 | 0,00057291 | 2,1333E-05 | Анализ результатов показывает, что при решении данной задачи метод Рунге-Кутта IV порядка является самым точным, на порядок хуже результаты у метода Рунге-Кутта III порядка. Метод предиктор-корректор точнее метода Эйлера, но намного уступает методам Рунге-Кутта III и IV порядка. Кроме того, 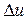 для каждого метода уменьшается с уменьшением шага сетки. для каждого метода уменьшается с уменьшением шага сетки.
|






 , где
, где 
 - точное решение
- точное решение














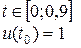

 . (1)
. (1)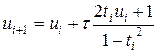 ,
,

 (2)
(2) .
.
 ,
, .
.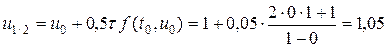



 (3)
(3)  (4)
(4)


 (5)
(5)  (6)
(6)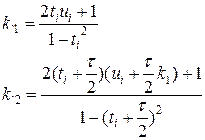



 для каждого метода уменьшается с уменьшением шага сетки.
для каждого метода уменьшается с уменьшением шага сетки.