 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пружинные механизмы уравновешивания
Общие сведения Уравновешивающие устройства служат для восприятия веса звеньев манипулятора и частично - веса перемещаемых им грузов, а также для компенсации влияния статических моментов масс звеньев робота. Неуравновешенность механизма приводит к увеличению погрешностей позицирования, динамических погрешностей, зависящих от скорости и ускорения движения, к увеличению нагрузок на опоры и потребляемой мощности. Из теории механизмов и машин известно, что условием уравновешивания механизма является постоянство главного вектора и главного момента сил давления стойки на фундамент или в кинематических парах:
Для выполнения первого из условий ( 3.1 ) необходимо и достаточно подобрать массы механизма так, чтобы общий центр масс ( ЦМ ) всех звеньев механизма оставался неподвижным, а для выполнения второго условия - подобрать массы механизма так, чтобы центробежные моменты инерции масс всех звеньев механизма были постоянными. Полностью исключить неуравновешенные силы очень сложно, а иногда и невозможно. Поэтому чаще всего ограничиваются устранением сил инерции. Уравновешивание путем распределения масс звеньев устраняющее давление cтойки на фундамент, называется уравновешиванием масс. Условия уравновешивания масс: Р = 0 . М = 0 . Если выполняется только первое условие, то уравновешивание называется статическим,если только второе - то моментным, а если оба - то динамическим. Обычно Р и М - периодические функции вращения начального звена механизма. Динамическое, уравновешивание также обычно осуществляется приближенно: устраняется лишь первая гармоника Р и М, при этом Р удается уменьшить в 5...10 раз, а - в десятки раз. В настоящее время разработаны методы автоматической балансировки. В роботах-манипуляторах чаще всего применяются статическое, уравновешивание, так как динамииеское уравновешивание очень трудно осуществить. Скорости движения здесь сравнительно невысоки и все динамические нагрузки воспринимает привод, что, конечно, ухудшает динамику робота. Грузовое уравновешивание Статическое уравновешивание выполняется противовесами, пружинами или пневмоцилиндрами. Конструкции грузовых уравновешивателей просты ( рис. 3.1 ). Они содержат постоянный или сменный груз I, который может перемещаться относительно оси вращения 2 на расстояние Н. Момент инерции противовеса определяется по известной теореме о параллельных осях:
где m - его масса. Этот момент инерции подбирается равным моменту инерции перемещаемого роботом груза 3. Введение противовеса увеличивает общий момент инерции всей системы, что приводит к ухудшению динамики робота. Одновременно снижаются чувствительность, легкость хода, затягиваются переходные процессы. Пружинные механизмы уравновешивания Наиболее широко применяются пружинные механизмы уравновешивания. В них используются пружины, работающие на растяжения – сжатие или кручение, связанные с уравновешиваемым звеном так, что при повороте этого звена и возрастании неуравновешенного момента увеличивается противодействующее усилие пружины, которая создаёт уравновешивающий момент. Проиллюстрируем этот способ на примере шарнира (рис. 2.2). Требуется определить параметры пружины (жесткость С, первоначальную длину h положения болтовых креплений на верхнем и нижнем звеньях и т.д.), при которых момент силы реакции пружины относительно оси шарнира равен по модулю и противоположен по направлению моменту, создаваемому силой тяжести. Пусть m - масса груза, переносимого роботом; l - длина звена от центра масс груза до оси вращения шарнира;
В соответствии с рис 3.2 имеем:
Момент силы тяжести массой m:
должен уравновеситься моментом
где ОЕ – плечо приложения силы F Учитывая, что
Подставив (3.3) и (3.6) в (3.5), получим:
Если , координаты точки крепления пружины в системе отсчёта, связанной с нижним звеном, то естественно положить Х=0 (рис3.2), так как при этом обеспечивается условие равновесия в вертикальном положении и одинаковое действие пружины относительно среднего положения Сопоставление выражений (3.4) и (3.7) показывает, что уравновешивание не может быть полным. Уравновешивание будет тем точнее, чем ближе ось сочленения к точке крепления пружины к нижнему звену и чем дальше от точки крепления пружины к верхнему (выходному) звену, т.е. при условии
Рисунок 3.1 – Схема грузового уравновешивающего механизма.
Рисунок 3.2 – Схема пружинного уравновешивающего механизма.
Рисунок 3.3 – Схема уравновешивающего механизма с активным цилиндром.
Рисунок 3.4 – Схема электромагнитного уравновешивающего механизма.
Задание 1. Определить момент инерции противовеса, если m=100 кг, Н=30мм 2. Определить параметры пружины если m=100кг, l=300мм, 3. Определить уравновешивающий момент по рисунку 3.3 по следующим данным: m=100кг, 4. |




 (3. 1)
(3. 1) ( 3.2. )
( 3.2. ) - собственный момент инерции противовеса;
- собственный момент инерции противовеса; - расстояние от точки крепления пружины на верхнем звене до оси;
- расстояние от точки крепления пружины на верхнем звене до оси; - расстояние от точки крепления пружины на нижнем звене до оси;
- расстояние от точки крепления пружины на нижнем звене до оси; - угол поворота звена манипулятора.
- угол поворота звена манипулятора.





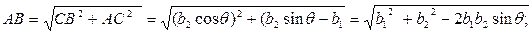 (3.3)
(3.3)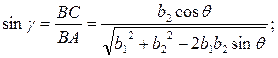

 (3.4)
(3.4) силы F пружины, причем
силы F пружины, причем (3.5)
(3.5) - изменение длины пружины;
- изменение длины пружины;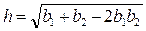 минимальная длина пружины, находим
минимальная длина пружины, находим (3.6)
(3.6) (3.7)
(3.7) .
.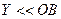 , или
, или  (3.8)
(3.8)





 =300мм, Y=100мм,
=300мм, Y=100мм,