ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Построение графиков поверхностей, заданных параметрически
ГРАФИКИ В MATLAB. ПОСТРОЕНИЕ ТРЕХМЕРНЫХ ГРАФИКОВ Цель работы: приобрести навыки построения трехмерных графиков в MatLab. График поверхности (трехмерный или 3D-график) – это график, положение точки в котором определяется значениями трех координат. Построение графиков поверхностей Декартовая система координат состоит из заданной фиксированной точкой пространства О, называемой началом координат, и трех перпендикулярных прямых пространства ОХ, OY, OZ, не лежащих в одной плоскости и пересекающихся в начале координат – их называют координатными осями (ОХ – ось абсцисс, OY – ось ординат, OZ – ось аппликат). Положение точки М в пространственной системе координат определяется значением трех координат и обозначается М(х,у,z). Три плоскости, содержащие пары координатных осей, называются координатными плоскостями XY, XZ, YZ. Величина z называется функцией двух переменных х и у, если каждой паре чисел, которые могут быть значениями переменных х и у, соответствует одно или несколько определенных значений величины z. При этом переменные хи у называют аргументами функции z(x, у).Пары тех чисел, которые могут быть значениями аргументов х, у функции z(x, у),в совокупности составляют область onределения функции. Для построения графика двух переменных z=f(x,y) необходимо выполнить следующие действия: 1. Сформировать в области построения графика прямоугольную сетку, проводя прямые, параллельные осям y=yj и x=xi, где xi=x0+ih, h=(xn-xo)/k, i=0,1,2,…,n, 2. Вычислить значения 3. Обратится к функции построения поверхности, передавая ей в качестве параметров сетку и матрицу Z=(zi,j) значений в узлах сетки. Функцияmeshgrid – для форматирования прямоугольной сетки. ПРИМЕР 1 Построить график функции z(x,y)=y2-x2, где х Для форматирования сетки воспользуемся функцией meshgrid.
После формирования сетки вычислим значение z во всех узлах.
Обратимся к функции mesh для построения графика: mesh(x,y). В результате чего будет построен трехмерный график (рис. 1).
Для получения менее грубого графика следует сетку делать более плотной (рис. 2).
Рис. 1График функции z(x,y) = y2 - x2
Рис. 2График функции z(x,y) = y2 - x2 с плотной сеткой
Функция surf – строит каркасную поверхность, заливая каждую ее клетку цветом, который зависит от значения функции в узлах сетки.
ПРИМЕР 2 Построить график функции [x,y] = meshgrid(-2:0.2:2,-2:0.2:2); z = sqrt (x.^2+y.^2); surf(x,y,z)
Рис. 3График функции В MatLab можно построить графики двух поверхностей в одной системе координат. Для этого, как и для плоских графиков, следует использовать команду hold on, которая блокирует создание второго нового окна при выполнении команд surfили mesh.
ПРИМЕР 3 Построить график функции z(x, у) = ±(х2 + y2) - 1. [x,y]=meshgrid(-2:0.2:2,-2:0.2:2); z=x.^2+y.^2-1; z1=-x.^2-y.^2-1; surf(x,y,z) hold on surf(x,y,z1)
Рис. 4График функции z(x, у) = ±(х2 + y2) - 1
Построение графиков поверхностей, заданных параметрически При построении графиков поверхностей, заданных параметрически: х(u, v), у(u, v) и z(u, v), необходимо построить матрицы X, Y и Z одинакового размера. Для этого массивы u и v должны быть одинакового размера. После этого следует выделить два основных вида представления х, у и z в случае параметрического задания поверхностей: 1. Если х, у и z представимы в виде f(u)*g(u), то соответствующие им матрицы X, Y и Z следует формировать в виде матричного умножения f(u) на g(u). 2. Если х, у и z представимы в виде f(u) или g(u), то в этом случае матрицы X, Y и Z следует записывать в виде f(u)ones(size(v)) или g(u)ones(size(u)) соответственно. ПРИМЕР 4 Построить поверхность однополостного гиперболоида, уравнение которого задано в параметрическом виде: х(u v) =ch(u)cos (v), y(u, v)= ch(u)sin (v), z(u, v)=sh(u). [u,v]=meshgrid(0:pi/50:2*pi); %Формируем матрицу X как матричное произведение ch(u)*cos(v) X=cosh(u).*cos(v); %Формируем матрицу Y как матричное произведение ch(u)*sin(v) Y=cosh(u).*sin(v); %Формируем матрицу Z как матричное произведение столбца sh(u) на строку %ones(size(v)) Z=sinh(u).*ones(size(v)); %Формируем график поверхности surf(X,Y,Z); grid on %Подписываем график и оси title('ГРАФИК ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА'); xlabel('X'); ylabel('Y'); zlabel('Z'); Общие принципы форматирования трехмерных графиков остаются теми же, что и в двумерном случае. Анимация При изучении движения точки на плоскости и в пространстве, MatLab позволит построить график движения и проследить за ним. Для построения анимационного ролика в MatLab существуют две функции: comet(х, у) и comet3(х,y,z). Функция comet(х, у) позволит увидеть движение точки вдоль кривой у(х) на плоскости, а функция comet3(х, у, z)позволит проследить за ее движением вдоль пространственной кривой z(x, у). ПРИМЕР 5 Движение точки на плоскости вдоль эллипса, который параметрически задается уравнением t=0:0.001:2*pi; x=cos(t); y=3*sin(t); comet(x,y); ПРИМЕР 6 Движение точки в пространстве вдоль винтовой линии, параметрическое уравнение которой имеет вид t=0:pi/500:10*pi; comet3(sin(t),cos(t),t)
Индивидуальные задания:
1. Построить графики поверхностей, заданных явно и параметрически; использовать встроенную функцию MatLab figure(n) для размещения программного кода в одном программном окне (a, p – номер компьютера; b,q – номер в списке группы; с – произвольное число). 2. Создать анимационный ролик, использовав при этом две любые функции из приведенных ниже. 3. Оформить протокол лабораторной работы.
|



 .
.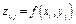 во всех узлах сетки.
во всех узлах сетки. [2,2], y
[2,2], y 




 .
.

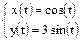 .
. .
.