 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Выводы по сравнительному анализу методов.
Анализ тестовых функций и построение линий уровня. Для анализа тестовых функций составим системы уравнений из частных производных и найдем стационарные точки: встака №1
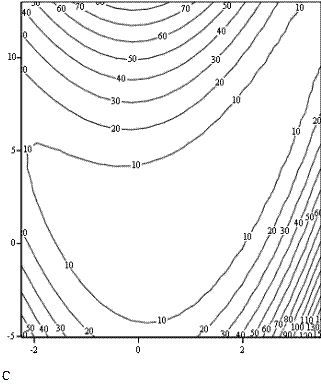
Линии уровня исследуемых функций представлены на рисунках 1,2 и 3 (стр.3). Рис. 1 - линии уровня функции f1(x) Рис.2 - линии уровня функции f2(x)
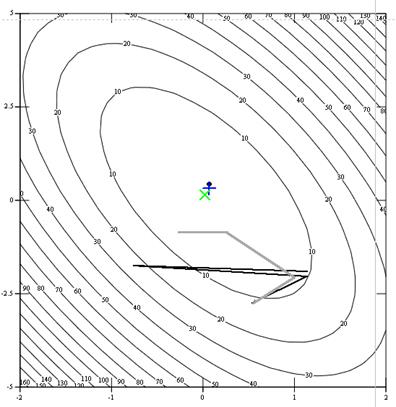
Рис.3 – линии уровня функции f3(x) Вычислительный эксперимент 1: минимизация методом S-квадрат и Нелдера-Мида. Воспользуемся данными, полученными в пункте 1/8, и готовыми программами S2_q.exe, S2_r.exe, NLMD_q.exe, NLMD_r.exe, введя заданные исходные данные, заполним первые три столбца таблицы 1 (стр 4). Программирование метода Хука-Дживса. Для реализации вычислительного эксперимента 2, были разработаны алгоритмы программ HKDV_q и HKDV_r для квадратичной формы и функции Розенброка соответственно. Листинги программ приведены в приложении. Полученные результаты внесены в 4ый столбец таблицы 1 (стр4), тем самым завершая ее заполнение. Разработав блок-схему, разработав, отладив и протестировав программу, провели вычислительный эксперимент 2, после чего заполнили четвертый столбец таблицы 1. Заполненная в процессе выполнения предыдущих пунктов таблица расположена на странице 4. Построение траекторий поиска минимума. Используя результаты работы программ S2_q.exe, NLMD_q.exe и HKDV_q.exe построим траектории поиска минимума на фоне линий для трех методов и функции f1(x), предварительно записав координаты 3 начальных итерации метода и конечной точки поиска. Для метода S-квадрат: 1. (0,5; -2,8); 2. (1,11; -2,18); 3. (-0,758; -1,83); 4. (0,275;-1,96). Для метода Нелдера-Мида: 1. (0,5; -2,8); 2. (1; -2,3); 3. (0,25; -1,3); 4. (-0.25; -1,3). Для метода Хука-Дживса: 1. (0,5; -2,8); 2. (-0.5; -3.8); 3. (0;0); 4. (0.5; -2.6). Полученный график представлен на рисунке 4., в котором на фоне линий уровня функции f1(x) нанесены следующие линии: черной линией показаны итерации поиска методом S-квадрат; серой линией – методом Нелдера-Мида; прерывистой линией – методом Хука-Дживса. Также на рисунок 4 нанесены конечные точки поиска минимума. Точкой обозначены координаты точки минимума, достигнутой - методом S-квадрат; косым крестом - Хука-Дживса; прямым крестом - Нелдера-Мида.
Рис.4. Итерации поиска различными методами. Таблица 1. Результаты минимизации
Выводы по сравнительному анализу методов. Очевидно, что, наименее точные результаты дает метод S-квадрат. К достоинствами этого метода можно отнести небольшое количество итераций и простоту программной реализации. Метод Хука-Дживса требует более сложной логической структуры, однако является наиболее точным. Задача № 1
Рис. 5. Усеченной конус, форму которого имеет бункер, можно считать полностью описанным в случае, если известна полная площадь поверхности и его объем. Поэтому, вычислим: 1) Площадь основания: Sосн =π∙r2; 2) Площадь боковой поверхности бункера: Sбок = π∙L∙ (R+r); 3) Полная площадь: Sпол= Sосн +Sбок= π(r2+ L∙ (R+r)); 4) Объем бункера: V = ⅓∙π∙h∙(r2+r∙R+R2), где R- радиус большего основания, r – радиус меньшего основания, при этом R и r будем считать известными, т.к. известны D и d, однозначно их определяющие. Опираясь на рисунок 5, можно выявить следующие зависимости: 1) По теореме Пифагора: L2 = h2 + (R-r)2 2) L∙cos(φ) = R-r. Таким образом, геометрическую форму бункера можно описать, используя различные наборы конструктивных параметров, например: (R, r, h); (L, h, r); (φ, h, r); (φ, h,R). Теперь найдем аналитически бункер минимальной стоимости. Известно, что стоимость материала основания 2 $/м2, а для боковой поверхности - 5 $/м2. Запишем целевую функцию в следующем виде: f(R,h,φ). Для этого предварительно вычислим: вставка 2, тогда f(R,h,φ) = 2S осн + 5Sбок = 2π(R-hctg(φ))2 + 5πh(2R - hctg(φ))/sin(φ). Воспользуемся условием, определяющим объём бункера. Вставка 3 (заодно проверь, не облажалась ли я при вычислениях) В конце еще раз выписать чему равен котангенс фи(выделено маркером)
На рисунке 6 представлены линии уровня данной функции.
Рис. 6. Линии уровня функции f(r,h) в области минимума. Для более точного определения точки минимума укрупним область наименьших значений: рисунок 7.
Рис. 7. Учитывая, что шаг по горизонтальной оси составляет 0.035, а по вертикальной – 0.05, то за точку минимума примем (12*0.035; 40*0.05) = (0.42; 2). Т.к. площадь внутри линии минимального уровня позволяет параметрам изменяться лишь незначительно, то с некоторой погрешностью решение можно признать однозначным. Таким образом, радиус верхнего основания 0,42 м и высоту бункера 2 метра можно считать квазиоптимальными значениями параметров при минимизации стоимости бункера объемом 10 м3. |
Метод минимизации Целевая функция
На рисунке 5 представлен бункер для хранения сыпучего материала без крышки, имеющий вид усеченного конуса, для которого необходимо решить задачу минимизации его стоимости.
Таким образом, была получена функция двух переменных:
, где
