 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основное уравнение динамики вращательного движения твердого тела 12
где М - суммарный момент внешних сил ( Второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально силе, действующей на тело, совпадает с ней по направлению и обратно пропорционально массе тела.
Основные расчетные формулы
Моменты инерций маятника Обербека: (при экспериментальном вычислении) где m – масса груза (кг), rо - радиус шкива (м), g - ускорение свободного падения (м/с2), h - путь, пройденный грузом за время t (м).
Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой
где J0 - момент инерции тела при r = 0. Из формулы (7) следует, что J = f(r2). Следовательно, если построить график этой функции в координатах J - r2, то должна получиться прямая, продолжение которой будет пересекать оси ординат в некоторой точке, соответствующей J0. Такое построение можно сделать приближенно, «на глаз». Однако математические методы обработки результатов наблюдения позволяют сделать такое построение достаточно точным. Наиболее просто это можно сделать, с помощью метода наименьших квадратов, вычислив J0 и Для удобства перепишем формулу (7) в виде
где r2 = х и 4m' = b. Метод наименьших квадратов позволяет найти J0 и b:
где
Абсолютная погрешность:
Средняя квадратичная ошибка:
Погрешности прямых измерений:
1. Времени - 2. Длины: 3. Массы -
Исходные данные
Таблицы с результатами измерений и вычислений
Таблица 1. Результаты измерений расстояний от оси вращения до центра масс грузов, времени прохождения пути груза, вычислений экспериментальных и теоретических моментов инерции маятника Обербека
Таблица 2. Результаты вычислений величин x, x2,
Вычисления
Пример вычислений для третьего опыта:
1) среднее время: 2) момент инерции экспериментальный:
3) момент инерции теоретический:
Значение моента инерции с учётом абсолютной ошибки:
Среднее квадратичное отклонение:
Доверительный интервал измерения момента инерции:
Построение графика
Вывод В ходе выполнения лабораторной работы был рассчитан момент инерции для крестовины с надетыми на нее грузиками. Величина момента инерции рассчитана для каждого из восьми измерений (причем сам опыт был проделан 24 раза, но значения времени усреднялись по тройкам). Момент инерции для этих измерений был получен двумя способами. Сравнение результатов при вычислении разными способами показало, что величины момента инерции, рассчитанные по-разному, имеют относительно небольшие различия между собой. Это подтверждено рассчитанным средним квадратичным отклонением:
12 |




 ), приложенных к телу относительно оси вращения; J - момент инерции тела (
), приложенных к телу относительно оси вращения; J - момент инерции тела (  ) относительно той же оси; e - угловое ускорение (
) относительно той же оси; e - угловое ускорение (  ).
). - 2 закон Ньютона в импульсной форме
- 2 закон Ньютона в импульсной форме , при m=const
, при m=const ,
, , если считать грузы материальными точками
, если считать грузы материальными точками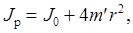 (7)
(7) , (8)
, (8) (9)
(9) число опытов; Ji - экспериментальное значение момента инерции Jэ, полученное для каждого опыта
число опытов; Ji - экспериментальное значение момента инерции Jэ, полученное для каждого опыта
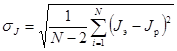
 (с)
(с)



 ,
,  ,
,  ,
,  ,
,  , где
, где
 - расстояние от оси вращения до центра масс грузов, J – момент инерции маятника Обербека.
- расстояние от оси вращения до центра масс грузов, J – момент инерции маятника Обербека.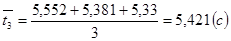


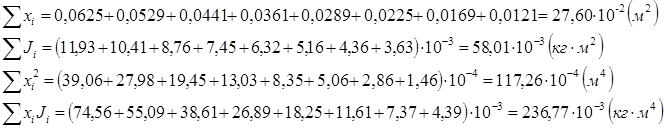








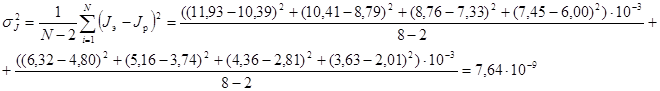



 . Также был построен график зависимости момента инерции от квадрата радиуса. Следует отметить, что исходя из самой формулы нахождения момента инерции и непосредственно графика, зависимость между этими величинами прямопропорциональна.
. Также был построен график зависимости момента инерции от квадрата радиуса. Следует отметить, что исходя из самой формулы нахождения момента инерции и непосредственно графика, зависимость между этими величинами прямопропорциональна.