 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИй ПРИ ИЗГИБЕ БАЛКИ
Цель работы:определить опытным путем величину прогиба двухопорной балки и сравнить его с теоретическим значением.
Оборудование и инструменты:лабораторный стенд для измерения прогибов балки (рис. 4.1), исследуемый образец, штангенциркуль, линейка.
Рис. 4.1. Лабораторный стенд для определения деформаций при изгибе балки: 1 − винтовой пресс ДМ-30С; 2 – двухопорное приспособление; 3 – исследуемый образец; 4 – маховик ускоренного перемещения штока; 5 − шток; 6 − динамометрическая скоба; 7 – стол пресса; 8 – штурвал механизма точного перемещения стола. Теоретические основы
Рассмотрим консольную балку, нагруженную на свободном конце сосредоточенной силой  (рис. 4.2). (рис. 4.2). Рис. 4.2. Деформации при изгибе консольной балки
Под действием внешней нагрузки балка деформируется, ее ось изгибается и приобретает форму, изображенную пунктирной линией. Упругую деформацию балки при изгибе характеризуют два параметра – прогиб и угол поворота поперечного сечения. Перемещение Угол В большинстве практических задач упругие деформации балки малы, поэтому принимают
где Изгибающий момент в произвольном сечении x равен Уравнение (3.1) принимает вид
Угол поворота поперечного сечения рованием выражения (3.2). При первом интегрировании определяют первую производную
При повторном интегрировании определяют прогиб
Получаем:
где Выражения (4.3) и (4.4) справедливы для любого произвольного сечения с координатой x, поэтому подставляем значения x, y, θ для точки, в которой эти значения известны. В заделке (точка О) Окончательное выражение для определения прогибов и углов поворота поперечных сечений консольной балки.
Рассмотрим еще один пример. Определить величину прогиба Для сохранения равновесия конструкции прикладываем в опорах А и В реакции
Аналогичные результаты легко получить из симметричности схемы нагружения балки. Запишем значение изгибающего момента
После подстановки (4.6) в (4.2) дифференциальное уравнение изогнутой оси двухопорной балки принимает вид
где  – осевой момент инерции сечения прямоугольной формы (рис.4.4). – осевой момент инерции сечения прямоугольной формы (рис.4.4).
Рис.4.3. Деформации при изгибе двухопорной балки
Интегрируя (4.7), получим уравнение углов поворота сечений
Интегрируем уравнение углов поворота (4.8), получаем уравнение прогибов
Укажем точки, в которых известен прогиб В (4.8) подставляем значения точки
Подставляем в (4.9) значения точки
Рис. 4.4. Поперечное сечение двухопорной балки
Окончательно уравнение (4.9) с учетом (4.10), (4.11) принимает вид
Уравнение (4.12) является аналитическим выражением, позволяющим определить прогиб в любом поперечном сечении балки (рис. 4.3). Для определения прогиба в точке
|





 центра тяжести произвольного поперечного сечения в направлении, перпендикулярном оси балки, называют прогибом
центра тяжести произвольного поперечного сечения в направлении, перпендикулярном оси балки, называют прогибом  .
. , на который повернется сечение относительно недеформированного положения, называется углом поворота поперечного сечения. Угол
, на который повернется сечение относительно недеформированного положения, называется углом поворота поперечного сечения. Угол  (угол поворота сечения
(угол поворота сечения  ). Исходя из этого, получено выражение, которое называется дифференциальным уравнением изогнутой оси балки.
). Исходя из этого, получено выражение, которое называется дифференциальным уравнением изогнутой оси балки. , (4.1)
, (4.1) – изгибающий момент в рассматриваемом сечении (индекс
– изгибающий момент в рассматриваемом сечении (индекс  соответствует оси, вокруг которой момент стремится повернуть конструкцию);
соответствует оси, вокруг которой момент стремится повернуть конструкцию); 
 – модуль упругости материала балки;
– модуль упругости материала балки;  – момент инерции сечения относительно оси
– момент инерции сечения относительно оси  ;
;  – жесткость балки при изгибе.
– жесткость балки при изгибе.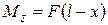 .
. (4.2)
(4.2) и, следовательно, угол поворота сечения
и, следовательно, угол поворота сечения 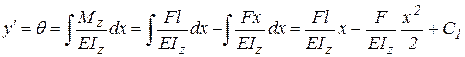 . (4.3)
. (4.3) .
.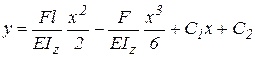 (4.4)
(4.4) и
и  − постоянные, которые находят следующим образом.
− постоянные, которые находят следующим образом. ,
, 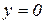 ,
,  и, следовательно,
и, следовательно,  .
. ,
,  (4.5)
(4.5) в середине пролета двухопорной балки (рис. 4.3), нагруженной силой
в середине пролета двухопорной балки (рис. 4.3), нагруженной силой  длина балки, размеры прямоугольного поперечного сечения
длина балки, размеры прямоугольного поперечного сечения 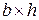 , мм (рис. 4.4).
, мм (рис. 4.4). и
и  . Реакции находим из уравнений равновесия, в качестве которых используем уравнения моментов относительно точек А и В
. Реакции находим из уравнений равновесия, в качестве которых используем уравнения моментов относительно точек А и В  ,
, 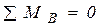 :
: ,
, .
.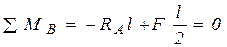 ,
, .
. в произвольном сечении, расположенном на расстоянии
в произвольном сечении, расположенном на расстоянии  от точки
от точки 
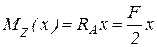 . (4.6)
. (4.6) , (4.7)
, (4.7)
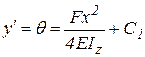 . (4.8)
. (4.8)
 . (4.9)
. (4.9) и
и  прогибы балки равны нулю
прогибы балки равны нулю  . В точке
. В точке  поперечное сечение не поворачивается
поперечное сечение не поворачивается  , так как изогнутая ось балки симметрична относительно этой точки. Для определения коэффициентов
, так как изогнутая ось балки симметрична относительно этой точки. Для определения коэффициентов  и
и  подставляем в (3.8) и (3.9) известные параметры точек
подставляем в (3.8) и (3.9) известные параметры точек  ,
,  (4.10)
(4.10) ,
, 
 . (4.11)
. (4.11) . (4.12)
. (4.12)
 . (4.13)
. (4.13)