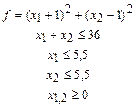ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Багатокритеріальна оптимізація
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ “КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ” МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ЛАБОРАТОРНИХ РОБІТ З КУРСУ “СПЕЦІЛЬНІ РОЗДІЛИ МАТЕМАТИКИ” ДИСКРЕТНА МАТЕМАТИКА І ОПТИМІЗАЦІЯ для студентів спеціальності “Технологія машинобудування ”
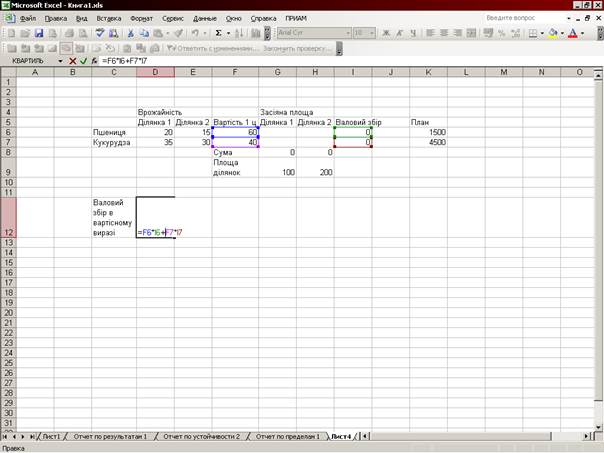
Київ НТУУ “КПІ” 2014 Зміст Лабораторна робота №1. Лінійне програмування 3 Лабораторна робота №2 Нелінійне програмування 11 Лабораторна робота №3 Динамічне програмування 18 Лабораторна робота №4 Багатокритеріальна оптимізація 34 Лабораторна робота №5 Стохастичний автомат 42 Лабораторна робота №5 Стохастичний автомат 42 Лабораторна робота №6 Мережне планування 56 Лабораторна робота №1 Лінійне програмування Мета. Навчитись формалізувати оптимізаційну задачу лінійного програмування і розв’язувати її графічним способом і за допомогою поширених ПЗ. Завдання. Згідно з варіантом виконати розв’язання задачі лінійного програмування графічним способом і за допомогою табличного редактора Excel. Склад звіту Завдання, розв’язання задачі графічним способом, розв’язання задачі за допомогою табличного редактора Excel. Приклад виконання роботи Задача. Господарство має дві ділянки (100 та 200 га) з різною врожайністю: на першій ділянці врожайність пшениці 20ц/га, на другій – 15ц/га; кукурудзи відповідно 35 і 30ц/га. План по пшениці – 1500ц, а кукурудзи – 4500. Ціна 1ц пшениці – 60, а кукурудзи – 40. Необхідно встановити площі посіву пшениці та кукурудзи на кожній ділянці для отримання максимального валового збору в вартісному виразі. Спочатку готуємо вихідні дані (див. рис. 1.1).
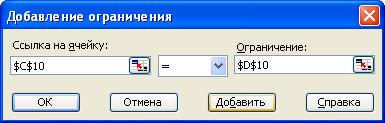
Рис.1.1. Підготовка вихідних даних В комірках G8 (G6+G7) і H8 (H6+H7) розміщуються формули розрахунку суми площі посіву на кожній ділянці, а в комірках I6 (G6*D6+H6*E6), I7 (=G7*D7+H7*E7) – формули розрахунку валового збору в натуральному вираження. В комірці D12 –розрахунок валового збору в вартісному вираженні. Після цього входимо в пункт меню «Сервис», потім вибираємо пункт «Поиск решения». З’являється діалогове вікно, яке показане на рис. 1.2. В ньому необхідно встановити посилання на комірку, в якій знаходиться формула цільової функції: «Установить целевую ячейку» і посилання на комірки, в яких повинен бути розміщений результат – невідомі, які ми шукаємо: «Изменяя ячейки». Також необхідно встановити мету оптимізації, в даному випадку «Максимальному значению». Після цього необхідно ввести обмеження. Для цього клацніть мишкою по кнопці «Добавить». З’явиться вікно введення обмежень (рис.1.3).
Рис. 1.2. Вікно завдання умов оптимізації (початковий стан)
Рис. 1.3. Вікно введення обмежень В лівій комірці розміщується посилання на комірку, в якій знаходиться розрахункова формула, в центрі – вид обмеження, а справа – значення обмеження чи посилання на комірку, в якому знаходиться це значення. На рис. 1.4 – 1.6 показані варіанти введення обмежень різного виду.
Рис. 1.4. Вікно введення обмежень (варіант)
Рис. 1.5. Вікно введення обмежень (варіант)
Рис. 1.6. Вікно введення обмежень (вибір виду обмеження) Після введення всіх даних форма має вигляд, приведений на рис. 1.7.
Рис. 1.7. Вікно завдання умов оптимізації (в стані заповнення всіх даних) Після цього необхідно клацнути по кнопці «Выполнить». Після виконання обчислень з’явиться вікно (рис.1.8).
Рис. 1.8. Вікно вибору форми звіту Після вибору в вікні «Тип отчета» клацніть по кнопці «ОК». Вибрані вами звіти будуть розміщені в новостворених листах. Форма різних видів звітів показана в табл. 1.1 – 1.3. Табл. 1.1. Звіт «Отчет по результатам»
Табл.. 1.2. Звіт «Отчет по устойчивости»
Табл.. 1.3. Звіт «Отчет по пределам»
Контрольні питання
Література 1. Разработка бизнес-приложений в экономике на базе MS EXCEL –М.: ДИАЛОГ_МИФИ, 2003. –416с. 2. С. Л. Лондар, Р, В. Юрковець Економетрія засобами MS EXCEL –К.: Європейський університет, 2004. –242с. 3. А. А. Мазаракі, Ю.А. Толбатов Математичне програмування в EXCEL –К.: Четверта хвиля, 1998.–208с. Варіанти завдань 1. 5. 9. 17.
21. 24. 28. 32. 40. 44. 48. Лабораторна робота №2 Нелінійне програмування Мета. Навчитись формалізувати оптимізаційну задачу нелінійного програмування і розв’язувати її за допомогою множників Лагранжа. Завдання. Згідно з варіантом виконати розв’язання задачі лінійного програмування методом множників Лагранжа. Склад звіту Завдання, розв’язання задачі»вручну», розв’язання задачі за допомогою табличного редактора Excel, висновки. Теоретичні відомості До нелінійного програмування відносять задачі, в яких цільова функція і/або обмеження виражені як нелінійні функції. Одним із способів розв’язання такої задачі є метод множників Лагранжа. Цей спосіб застосовується в тому випадку, коли обмеження мають вигляд рівнянь. Нехай цільова функція Для розширення застосування методу множників Лагранжа обмеження в вигляді нерівностей можливо привести до обмежень в формі рівнянь. Приклади таких формул, приведені в табл..2.1. Таблиця 2.1. Формули перетворень обмежень-нерівностей до обмежень-рівнянь
Завдання. Необхідно мінімізувати загальні витрати Будуємо функцію Лагранжа
Продиференцювавши її за трьома невідомими, отримуємо нелінійну систему з трьох рівнянь
Для розв’язання в середовищі Excel спочатку необхідно підготувати вихідні дані. Приклад їх підготовки приведено в табл..2.2 і 2.3. Таблиця 2.2. Приклад підготовки вихідних даних
Таблиця 2.3. Приклад підготовки вихідних даних з формулами
Після цього входимо в пункт меню «Сервис», потім вибираємо пункт «Поиск решения». З’являється діалогове вікно, яке показане на рис. 1.2. В ньому необхідно встановити посилання на комірку, в якій знаходиться формула цільової функції: «Установить целевую ячейку» і посилання на комірки, в яких повинен бути розміщений результат – невідомі, які ми шукаємо: «Изменяя ячейки». Також необхідно встановити мету оптимізації, в даному випадку «Максимальному значению». Після цього необхідно ввести обмеження. Для цього клацніть мишкою по кнопці «Добавить». З’явиться вікно введення обмежень (приклади рис.2.1–2.3).
Рис.2.1. Встановлення як обмеження рівняння з системи.
Рис. 2.2. Встановлення обмеження суми
Рис.2.3. Встановлення обмеження значень параметру більше 0. З введеними всіма даними форма має вигляд, приведений на рис.2.4. Додаткові параметри оптимізації можна задати, вибравши кнопку «Параметры», в формі, показаній на рис.2.6.
Рис.2.4. Вигляд форми з усіма введеними даними Після цього необхідно клацнути по кнопці «Выполнить». Після виконання обчислень з’явиться вікно (рис.2.5).
Рис.2.5.
Рис.2.6. Завдання параметрів пошуку розв’язку Після вибору в вікні «Тип отчета» клацніть по кнопці «ОК». Вибрані вами звіти будуть розміщені в новостворених листах. Форма різних видів звітів показана в табл. 2.4 – 2.6. Таблиця 2.4. Форма звіту про результати оптимізації
Таблиця 2.5.
Таблиця 2.6.
Контрольні питання
Література 1. Кузьмичов А.І., Медведєв М.Г. Математичне програмування в Excel: Навч. Посіб. – К.:Вид-во Європ. Ун-ту, 2005. –320с. Варіанти завдань
26. f=(x1-3)2+(x2-5)2; x2-2x1=5; x12+x22<=10 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. Лабораторна робота №3 Динамічне програмування Мета. Навчитись формалізувати оптимізаційну задачу динамічного програмування і розв’язувати її. Завдання. Згідно з варіантом виконати розв’язання задачі динамічного програмування. Склад звіту Завдання, послідовність таблиць розв’язання задачі, висновки. Теоретичні відомості Алгоритм
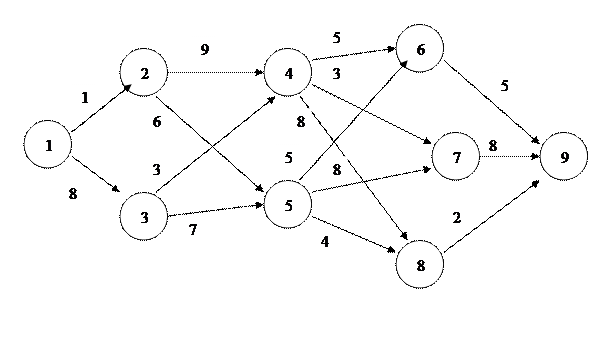
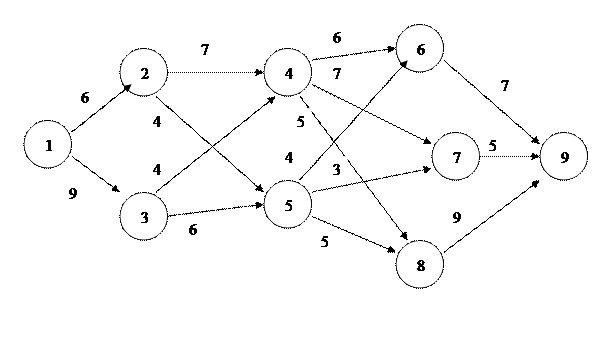
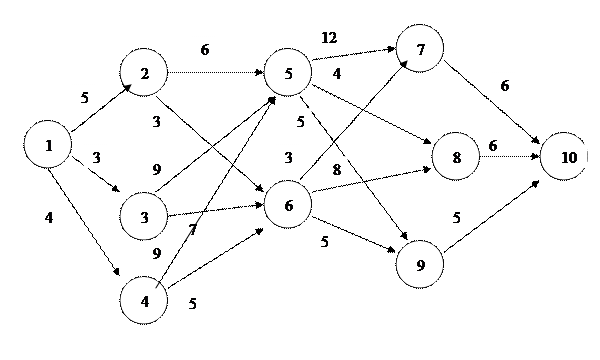
Приклад виконання роботи На рис.3.1 представлений граф задачі динамічного програмування.
Рис. 3.1. Граф задачі динамічного програмування Спочатку розіб’ємо вершини на сукупність етапів (табл..3.1). Таблиця 3.1. Етапи
Нехай вартість перевезення з вершини S в вершину J є вагою відповідної дуги, Fn(s) мінімальні затрати на перевезення з S в кінцеву, якщо до кінцевої n етапів; Jn(S) номер вершини, через яку потрібно рухатись на етапі n, щоб вартість була Fn(s). Вершина 10 є останньої. Для попереднього до неї етапу таблиця 3.2 показує пошук умовно оптимального рішення. Таблиця 3.2. Крок 1
Таблиці 3.3 – 3.5 показують наступні кроки пошуку оптимізації Таблиця 3.3. Крок 2.
Таблиця 3.4. Крок 3.
Таблиця 3.5. Крок 4.
Після того, як ми дійшли до вихідної вершини, необхідно, почавши з цієї вершини побудувати маршрут до кінцевої по вершинам, які відповідають умовно-оптимальним рішенням. В даному випадку це буде 1–>2–>6–>9–>10. Цей маршрут і буде відповідати мінімальній вартості, яка вже отримана як F3(s)=16. Варіанти завдань 1.
2.
3.
4. 5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
Контрольні питання
Література 1. Кузнецов А.В., Холод Н.И., Костевич Л.С. Руководство к решению задач по математическому программированию –Мн.: Вышэйш. школа, 1978. –256с. Лабораторна робота №4 Багатокритеріальна оптимізація Мета. Навчитись формалізувати і розв’язувати задачу багатокритеріальної оптимізації. Завдання. Вам необхідно підготувати свою задачу по багатокритеріальному вибору. В ній повинно бути не менш як 6-7 об`єктів, що порівнюються між собою по 5-6 чи більшій кількості показників. До початку роботи з програмою потрібно провести формалізацію задачі, результатом якої будуть дві таблиці. Одна з них повинна містити список всіх об`єктів, значення показників для кожного об`єкту та мету оптимізації по кожному показнику окремо, тобто яке значення даного показника вважається найкращим – мінімальне чи максимальне. Ця таблиця має наступну форму (табл. 2.1). Таблиця 2.1.
Оскільки в реальних задачах значимість окремих показників для оцінки якості об`єкту різна, то необхідно підготувати таблицю попарного порівняння, буде використана для розрахунку вагових коефіцієнтів (дивись таблицю 2.2). В кожній графі таблиці повинно бути записано значення порівняння двох критеріїв (наприклад, еквівалентно, важливіше тощо). Звертаємо вашу увагу, що ця таблиця не симетрична і порівняння потрібно проводити в напрямку, вказаному стрілкою. Це означає, що в графі, де розміщена стрілка порівнюється “Критерій 2” з “Критерієм 3”, але не навпаки. Враховуючи, використання 9 градацій (як в таблиці 5.1 вимагає певного досвіду та навиків), в лабораторній роботі використовуються тільки три градації порівняння: “А важливіше В”, “В важливіше А”, “А і В рівнозначні ”. Таблиця 2.2
Розв’язати задачу методом введення метрики в простір критеріїв за допомогою спеціального макросу. Склад звіту. Завдання, підготовлені вихідні дані для багатокритеріального вибору з їх описом, результати оптимізації. Приклад виконання роботи. Всі розрахунки виконуються в табличному редакторі Excel за допомогою спеціально розроблених макросів. Тому перед початком роботи необхідно завантажити файл (OW.XLS), в якому є необхідні модулі багатокритеріального вибору. Спочатку необхідно розрахувати вагові коефіцієнти за допомогою методу попарного порівняння. Для цього потрібно послідовно вибрати пункти меню « Сервис» , «Макрос», «Макросы». В вікні, що з’явилося після цього необхідно вибрати макрос Ch_Weight. Потім з’являється вікно (рис. 4.1).
Рис. 4.1 Запит назв критеріїв Вам необхідно відмітити поля, в яких ви внесли назви критеріїв. Після цього з’являється вікно приведене на рис.4.2, в якому ви повинні вказати комірку, з якої почнеться виведення результату.
Рис. 4.2 Запит місця виводу результату Після цього макрос буде запитувати для кожної можливої комбінації пар критеріїв буде запитувати відносно їх взаємної значущості (рис. 2.3).
Рис. 4.3 Запит про взаємну значущість Як відповідь ви мусите вибрати той з критеріїв, який на вашу думку більш важливий, або “Рівнозначні”. Після отримання всіх відповідей макрос видає таблицю вагових коефіцієнтів (табл. 4.3) Таблиці 4.3. Результати роботи макросу попарного порівняння
Після цього в табличному редакторі Excel необхідно підготувати дані. Приклад підготовки даних приведено на рис. 4.4
Рис. 4.4 Приклад підготовки вихідних даних Потім потрібно запустити макрос. Для цього потрібно послідовно вибрати пункти меню « Сервис» , «Макрос», «Макросы». В вікні, що з’явилося після цього необхідно вибрати макрос OptObjCh. Після запуску макросу необхідно відповідати та вводити інформацію через відповідні діалогові вікна. Спочатку необхідно відмітити той масив комірок, в якому для кожного критерію задається окрема ціль оптимізації, тобто min, або max (рис.4.5).
Рисунок 4.5. Запит на введення цілей Потім вводиться посилання на масив вагових коефіцієнтів, що були попередньо розраховані (рис. 4.6).
Рисунок 4.6. Запит на введення вагових коефіцієнтів Далі вводяться посилання на масиви назв критеріїв якості і масив назв об’єктів (рис. 4.7 та 4.8 відповідно).
Рисунок 4.7. Введення назв критеріїв якості
Рисунок 4.8. Введення назв об’єктів Після цього вводиться посилання на таблицю, яка містить вихідні дані для оптимізації (рис. 4.9).
Рисунок 4.9. Введення масиву даних Останнім вводиться посилання на місце таблиці, починаючи з якого буде виводитися результат (рис. 4.10).
Рисунок 4.10. Запит на місце виведення результату Даний макрос виконує ще дві операції, тому після вказаного запиту він пропонує обчислити резерв оптимізації (рис. 4.11). Після цього з’являється запит про проведення порівняння двох об’єктів (рис. 4.12). При ствердній відповіді необхідно буде ввести посилання на імена об’єктів, які ви хочете порівнювати (рис. 4.13 та 4.14).
Рисунок 4.11. Запит на необхідність обчислення резерву оптимізацїї
Рисунок 4.12. на необхідність обчислення резерву оптимізацїї
Рисунок 4.13. Запит першого об’єкту для порівняння
Рисунок 4.14. Запит другого об’єкту для порівняння Результат роботи макросу по ранжуванню об’єкті приведено в таблиці 4.4. Таблиця 4.4 Результати ранжування об’єктів (фрагмент)
Якщо ви відповіли ствердно на запитання про резерв оптимізації, то буде отримана таблиця виду 4.5. Для кожного об’єкту для кожного критерію вказане можливе збільшення його рейтингу, якщо даний критерій довести до оптимального значення. Таблиця 4.5 Результати обчислення резерву оптимізації (фрагмент).
Якщо ви відповіли ствердно на запит про порівняння двох об’єктів, то отримаєте результат порівняння як таблицю виду 4.6. В ній для кожного критерію вказане відставання в мірі рейтингу (комплексного критерію). Таблиця 4.6 Порівняння двох об’єктів
Після закінчення цього етапу роботи можливе моделювання параметрів з метою визначення можливості підвищення рейтингу об`єкту та затрат, необхідних для цього. Контрольні питання 1. Існуючі підходи до проблеми багатокритеріальної оптимізації. 2. Метод лінійної згортки критеріїв. 3. Суть методу введення метрики в простір критеріїв. 4. Чому неефективне завдання вагових коефіцієнтів експертом? 5. Суть методу попарних порівнянь. Література 1. С.Н. Лапач, А.В. Чубенко, П.Н. Бабич Статистика в науке и бизнесе –К.: 2002, Морион. – 640с. Лабораторна робота №5 |










 2.
2.  3.
3.  4.
4. 
 6.
6.  7.
7.  8.
8. 
 10.
10.  11.
11.  12.
12.  13.
13.  14.
14.  15.
15.  16.
16. 
 18.
18.  19.
19. 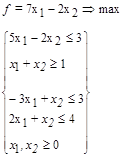 20.
20. 
 22.
22.  23.
23. 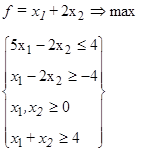
 25.
25. 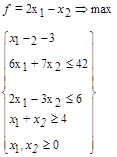 26.
26.  27.
27. 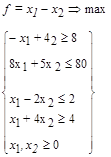
 29.
29.  30.
30.  31.
31. 
 33.
33. 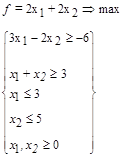 34.
34.  35.
35. 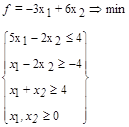 36.
36.  37.
37.  38.
38.  39.
39. 
 41.
41.  42.
42.  43.
43. 
 45.
45. 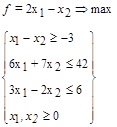 46.
46.  47.
47. 
 49.
49.  50.
50. 
 , а обмеження має вигляд
, а обмеження має вигляд  . Тоді для знаходження умовного екстремуму будується функція Лагранжа
. Тоді для знаходження умовного екстремуму будується функція Лагранжа 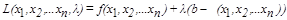 . Таким чином тепер ми можемо розв’язувати задачу як пошук безумовного екстремуму. Взявши часткові похідні по всім невідомим (включаючи l), ми отримаємо систему нелінійних в загальному випадку рівнянь, розв’язок яких дозволить оптимізувати цільову функцію.
. Таким чином тепер ми можемо розв’язувати задачу як пошук безумовного екстремуму. Взявши часткові похідні по всім невідомим (включаючи l), ми отримаємо систему нелінійних в загальному випадку рівнянь, розв’язок яких дозволить оптимізувати цільову функцію.











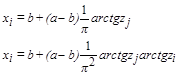




 Приклад виконання роботи
Приклад виконання роботи , якщо залежність окремих витрат від параметрів обчислюється за формулами
, якщо залежність окремих витрат від параметрів обчислюється за формулами  і
і  , а на значення параметрів накладається наступне обмеження
, а на значення параметрів накладається наступне обмеження  . Крім того фізично значення параметрів не можуть бути менше нуля.
. Крім того фізично значення параметрів не можуть бути менше нуля.