ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Простые числа. Генерация простых чисел 12
Простым называют целое число, больше единицы, единственными множителями которого является 1 и оно само. В криптографии, особенно криптографии с открытым ключом, нередко используют большие простые числа (512 бит и даже больше). Для исполнения алгоритмов с открытым ключом также необходимы простые числа. Генерация случайных чисел с последующей попыткой их разложения на множители из-за большого времени вычислений - тупиковый путь поиска простых чисел. Правильный путь - это генерация случайных чисел и последующая проверка, не являются ли они простыми. Существуют различные вероятностные тесты, определяющие с заданной степенью достоверности факт простоты числа. Если «степень достоверности» будет достаточна, то такие тесты достаточно надежны. Причем, если по какой-то причине понадобится большая достоверность простоты числа, можно установить меньший уровень вероятности ошибки. С другой стороны, если установить вероятность ошибочного прохождения теста составным числом в 300 миллионов раз меньшей вероятности выигрыша главного приза в государственной лотерее, о возможности ошибки можно не беспокоиться. Одним из широко используемых является следующий относительно простой алгоритм, разработанный Майклом Рабином (Michael Rabin). Вероятность прохождения этого теста составным числом убывает с ростом числа итераций. Гарантируется, что три четверти возможных значений а окажутся свидетелями простоты числа. Это означает, что составное число ошибочно пройдет t тестов с вероятностью не более (1/4)t, где t - число итераций. Алгоритм RSA Алгоритм RSA был предложен тремя изобретателями – Роном Ривестом (Ron Rivest), Ади Шамиром (Adi Shamir) и Леонардом Адлеманом (Leonard Adlenman) и является полноценным алгоритмом с открытым ключом, который можно использовать и для шифрования, и для создания цифровых подписей. Безопасность алгоритма RSA основана на трудоемкости разложения на множители (факторизации) больших чисел. Открытый и закрытый ключи являются функциями двух больших простых чисел разрядностью 100 - 200 десятичных цифр или даже больше. Предполагается, что восстановление открытого текста по шифротексту и открытому ключу равносильно разложению числа на два больших простых множителя. Для генерации двух ключей применяются два больших случайных простых числа р и q. Для максимальной безопасности р и q должны иметь равную длину. Рассчитывается произведение n=pq Затем случайным образом выбирается ключ шифрования е, такой что е и (p-1)(q-1) являются взаимно простыми числами. Затем, с помощью расширенного алгоритма Евклида вычисляется ключ расшифрования d такой, что
Другими словами,
Заметим, что d и e также взаимно простые числа. Числа е и n - это открытый ключ, а число d - закрытый. Два простых числа p и q больше не нужны. Они могут быть отброшены, но не должны быть раскрыты. При шифровании сообщение т сначала разбивается на цифровые блоки, размерами меньше п (для двоичных данных выбирается самая большая степень числа 2, меньшая п). То есть, если p и q являются 100-разрядными простыми числами, то п будет содержать около 200 разрядов, и каждый блок сообщения т должен быть около 200 разрядов в длину. Зашифрованное сообщение с будет состоять из блоков с той же самой длины. Формула зашифрования выглядит следующим образом:
При расшифровке сообщения для каждого зашифрованного блока
Так как
Таблица 1. Шифрование RSA
Точно также сообщение может быть зашифровано с помощью d, а расшифровано с помощью е, тут возможен любой выбор. Практическая часть
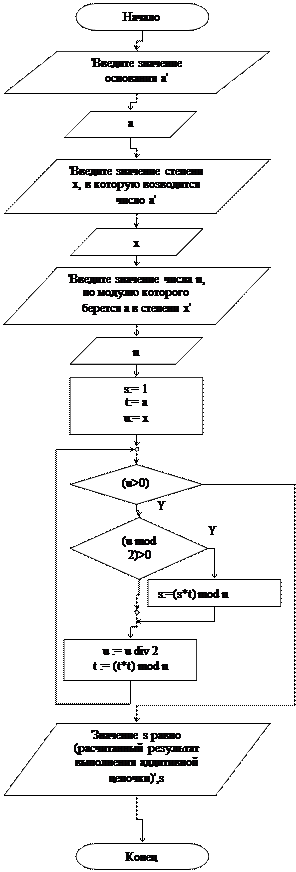
Блок-схема алгоритма:
Program Additional_Chain; Uses Crt; var a,x,n, s,t,u:integer; begin Clrscr; Writeln(‘Введите значение основания а’); Readln(a); Writeln(‘Введите значение степени х, в которую возводится число а’); Readln(x); Writeln(‘Введите значение числа n, по модулю которого берется а в степени х’); Readln(n); s:= 1; t:= a; u:= x; while (u>0) do begin if (u mod 2)>0 then s:=(s*t) mod n; u := u div 2; t := (t*t) mod n; end; Writeln('Значение s равно (рассчитанный результат выполнения аддитивной цепочки)',s); end.
(Примечание: все программные коды написаны в среде Pascal ABC)
Результат выполнения программы:
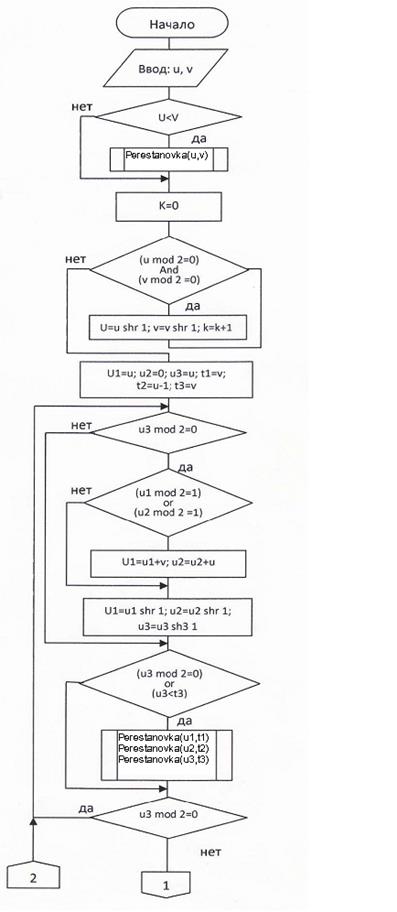
Программа: Program Algoritm_Evklida; Uses Crt; label vozvrat; var u,v,k,u1,u2,u3,t1,t2,t3:integer; procedure Perestanovka(var p1,p2:integer); var Bufer:integer; begin Bufer:=p1; p1:=p2; p2:=Bufer; end; begin Clrscr; Writeln('*Эта программа служит для поиска обратного значения по модулю ("x" из "(u*x) mod v = 1")*'); Writeln('Введите значение числа u'); Readln(u); Writeln('Введите значение числа v, по которому бурутся модуль'); Readln(v); if u<v then Perestanovka(u,v); k:=0; while ((u mod 2=0) and (v mod 2=0)) do begin u:=u shr 1; v:=v shr 1; k:=k+1; end; u1 := 1; u2 := 0; u3 := u; t1 := v; t2 := u-1; t3 := v; vozvrat: if (u3 mod 2=0) then begin if ((u1 mod 2=1) or (u2 mod 2=1)) then begin u1:=u1+v; u2:=u2+u; end; u1:=u1 shr 1; u2:=u2 shr 1; u3:=u3 shr 1; end; if ((t3 mod 2=0) or (u3 < t3)) then begin Perestanovka(u1,t1); Perestanovka(u2,t2); Perestanovka(u3,t3); end; if (u3 mod 2=0) then goto vozvrat; while ((u1 < t1) or (u2 < t2)) do begin u1:=u1+v; u2:=u2+u; end; u1:=u1-t1; u2:=u2-t2; u3:=u3-t3; if (t3>0) then goto vozvrat; while ((u1 >= v) and (u2 >= u)) do begin u1:=u1-v; u2:=u2-u; end; u1:=u1 shl k; u2:=u2 shl k; u3:=u3 shl k; Writeln('Результат поиска, x=',u-u2); end. Результат выполнения программы:
Program Proverka_pr_chisel; Uses Crt; label 10,13; var p,t,a,k,b,b2,m,j,z,newt,newu:integer; r:boolean; begin Randomize; Writeln('Введите число для проверки, является ли оно простым (p)'); Readln(p); k:=p - 1; b:=0; b2:=1; while (k mod 2=0) do begin b := b + 1; b2:=b2 shl 1; k:=k shr 1; end; m := (p-1) div b2; t:=8; r:=true; 10: a:=random(p); j:=0; z:=1; newt:=a; newu:=m; while (newu>0) do begin if (newu mod 2)> 0 then z:=(z*newt) mod p; newu:=newu div 2; newt:=(newt*newt) mod p; end; if b=0 then begin r:=false; Writeln('Число не является простым’); exit; end; if ((z = 1) or (z = p - 1)) then begin if r=false then Writeln('Число не является простым') else Writeln('Число является простым'); exit; end; 13: if ((j > 0) and (z = 1)) then begin r:=false; Writeln('Число не является простым'); exit; end; j := j + 1; if j<b then if (z <> (p-1)) then z:=(z*z) mod p else begin if r=false then Writeln('Число не является простым') else Writeln('Число является простым'); exit; end; if j<>b then goto 13; if ((j = b) and (z <> (p-1))) then begin r:=false; Writeln('Число не является простым'); exit; end; t:=t-1; if t<>0 then goto 10; if r=false then Writeln('Число не является простым') else Writeln('Число является простым'); end.
Результат выполнения программы:
4. Алгоритм RSA
Данная программа объединяет в себе все ранее рассмотренные.
Program RSA; Uses Crt; Function Addit_Ch(a,x,n:longint):longint; var s,t,u:longint; begin s:= 1; t:= a; u:= x; while (u>0) do begin if (u mod 2)>0 then s:=(s*t) mod n; u := u div 2; t := (t*t) mod n; end; Addit_Ch:=s; end;
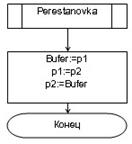
procedure Perestanovka(var p1,p2:longint); var Bufer:longint; begin Bufer:=p1; p1:=p2; p2:=Bufer; end;
Function Alg_Evk(u,v:longint):longint; label vozvrat; var k,u1,u2,u3,t1,t2,t3:longint; begin if u<v then Perestanovka(u,v); k:=0; while ((u mod 2=0) and (v mod 2=0)) do begin u:=u shr 1; v:=v shr 1; k:=k+1; end; u1 := 1; u2 := 0; u3 := u; t1 := v; t2 := u-1; t3 := v; vozvrat: if (u3 mod 2=0) then begin if ((u1 mod 2=1) or (u2 mod 2=1)) then begin u1:=u1+v; u2:=u2+u; end; u1:=u1 shr 1; u2:=u2 shr 1; u3:=u3 shr 1; end; if ((t3 mod 2=0) or (u3 < t3)) then begin Perestanovka(u1,t1); Perestanovka(u2,t2); Perestanovka(u3,t3); end; if (u3 mod 2=0) then goto vozvrat; while ((u1 < t1) or (u2 < t2)) do begin u1:=u1+v; u2:=u2+u; end; u1:=u1-t1; u2:=u2-t2; u3:=u3-t3; if (t3>0) then goto vozvrat; while ((u1 >= v) and (u2 >= u)) do begin u1:=u1-v; u2:=u2-u; end; u1:=u1 shl k; u2:=u2 shl k; u3:=u3 shl k; Alg_Evk:=u-u2; end;
Function ProvChet(a:longint):boolean; begin if (a mod 2=0) then ProvChet:=true else ProvChet:=false; end;
Function Pr_pr_ch(p:longint):boolean; label 10,13; var t,a,k,b,b2,m,j,z,newt,newu:longint; begin Randomize; k:=p - 1; b:=0; b2:=1; while (k mod 2=0) do begin b := b + 1; b2:=b2 shl 1; k:=k shr 1; end; m := (p-1) div b2; t:=8; Pr_pr_ch:=true; 10: a:=random(p); j:=0; z:=1; newt:=a; newu:=m; while (newu>0) do begin if (newu mod 2)> 0 then z:=(z*newt) mod p; newu:=newu div 2; newt:=(newt*newt) mod p; end; if b=0 then begin Pr_pr_ch:=false; exit; end; if ((z = 1) or (z = p - 1)) then begin exit; end; 13: if ((j > 0) and (z = 1)) then begin Pr_pr_ch:=false; exit; end; j := j + 1; if j<b then if (z <> (p-1)) then z:=(z*z) mod p else begin exit; end; if j<>b then goto 13; if ((j = b) and (z <> (p-1))) then begin Pr_pr_ch:=false; exit; end; t:=t-1; if t<>0 then goto 10; end;
Procedure Vzaimno_Pr_chisla; Var i:byte; Rez:array[1..3] of longint; pp:longint; znak,znak1,znak2 : Boolean; Begin Randomize; Znak1:=false; While znak1=false do Begin For i:=1 to 3 do Begin Pp:=10000+random(10000); Znak:=false; While znak=false do Begin Znak:=Pr_pr_ch(pp); If znak=true then Rez[i]:=pp; Znak2:=false; While znak2=false do Begin Pp:=pp+1; If ((pp mod 2=0) or (pp mod 3=0) or (pp mod 5=0) or (pp mod 7=0) or (pp mod 11=0) or (pp mod 13=0) or (pp mod 17=0) or (pp mod 19=0)) then znak2:=false Else znak2:=true; End; End; End; If (((Rez[1]-1)*(Rez[2]-2)) mod Rez[3] <>0) and (Rez[1]<>Rez[2]) and (Rez[1]<>Rez[3]) and (Rez[2]<>Rez[3]) Then znak1:=true; End; Writeln('Числа ', Rez[1],' ',Rez[2],' ', Rez[3],' ', 'являются взаимно простыми'); Readln; End;
Function Simple(n: integer):Boolean; Var i:integer; Begin Simple:=true; For i:=2 to (n div 2)+1 do Begin If n mod i=0 then Begin Simple:=false; Break; End; End; End;
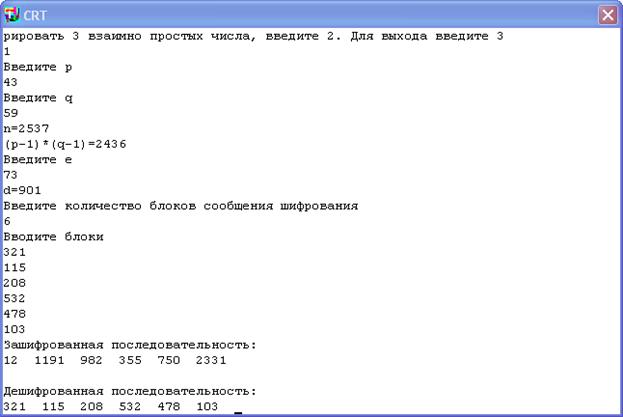
Var p,q,e,n,n1,d:longint; mo,co,moc:array[1..10] of longint; kb,i:integer; a,b,c:Boolean; enter:byte; Begin Clrscr; Writeln(‘Если Вы хотите произвести шифрование данных, введите 1, если Вам необходимо сгенерировать 3 взаимно простых числа, нажмите 2. Для выхода нажмите 3'); Readln(enter); if enter=1 then begin Repeat Begin Writeln(' Введите p'); Readln(p); a:=Simple(p); End Until a=true; Repeat Begin Writeln('Введите q'); Readln(q); b:=Simple(q); End Until b=true; n:=p*q; n1:=(p-1)*(q-1); Writeln('n=',n); Writeln('(p-1)*(q-1)=',n1); Repeat Begin Writeln('Введите e'); Readln(e); c:=Simple(e); End; Until c=true; d:=Alg_Evk(e,n1); Writeln('d=',d); Writeln('Введите количество блоков сообщения шифрования'); Readln(kb); Writeln('Введите блоки'); For i:=1 to kb do Readln(mo[i]); For i:=1 to kb do Co[i]:=Addit_Ch(mo[i],e,n); Writeln('Зашифрованная последовательность:'); For i:=1 to kb do Write(co[i],' '); Readln; For i:=1 to kb do Moc[i]:=Addit_Ch(co[i],d,n); Readln; Writeln('Дешифрованная последовательность:'); For i:=1 to kb do write(moc[i],' '); Readln; Readln; end; if enter=2 then Vzaimno_Pr_Chisla else exit; End.
Результат выполнения программы:
Вывод:в ходе выполнения данной лабораторной работы были закреплены на практике теоретические знания основ работы с алгоритмом шифрования RSA, который, в свою очередь, объединяет такие подразднлы, как вычисление степени числа по модулю другого числа, вычисление обратного значения по модулю, а также проверка чисел на правильность и генерация правильных чисел. 12 |



 .
. .
. .
. вычисляется
вычисляется .
.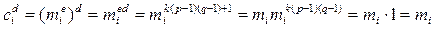 , все операции по (mod n), то формула восстанавливает сообщение. Сказанное выше суммировано в табл. 1.
, все операции по (mod n), то формула восстанавливает сообщение. Сказанное выше суммировано в табл. 1. .
.