ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Использование моста Сотти для экспериментального определения емкости конденсатора и вывод рабочей формулы
ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЕМКОСТИ КОНДЕНСАТОРА Методические указания к лабораторной работе №8 по физике
(Раздел «Электричество»)
Ростов-на-Дону 2011
Составители: Т.П. Жданова, А.Б. Гордеева, И.Г. Попова, Е.С. Богославская
УДК 530.1
ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЕМКОСТИ КОНДЕНСАТОРА: метод. указания к лабораторной работе № 8 - Ростов н/Д: Издательский центр ДГТУ, 2011.-9с.
Указания содержат краткое описание рабочей установки и методики определения электроемкости конденсатора методом моста Сотти. Методические указания предназначены для студентов инженерных специальностей всех форм обучения в лабораторном практикуме по физике (раздел «Электричество»).
Печатается по решению методической комиссии факультета «Нанотехнологии и композиционные материалы»
Научный редактор к.ф.-м.н., доц. Г. Ф. Лемешко
© Издательский центр ДГТУ, 2011
ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЕМКОСТИ КОНДЕНСАТОРА Цель работы: 1. Ознакомление с мостовым методом измерения электрической емкости конденсатора. 2. Определение законов сложения емкостей при параллельном и последовательном соединении конденсаторов. Оборудование: источник переменного тока, магазин эталонных конденсаторов, измеряемые неизвестные конденсаторы, осциллограф, реохорд (реостат, включенный как потенциометр).
Теоретическая часть Если уединенному проводнику сообщить электрический заряд
электрическая емкость уединенного проводника. Единица ёмкости – фарад (Ф). Конденсатором называется система из двух близко расположенных проводников (обкладок), разделенных слоем диэлектрика. В зависимости от формы обкладок конденсаторы бывают плоские, цилиндрические и сферические. Под емкостью
Электроемкость конденсатора зависит от его формы, геометрических размеров и диэлектрической проницаемости среды, заполняющей пространство между обкладками. В случае плоского конденсатора
где Другой важнейшей характеристикой конденсатора является напряжение пробоя, т.е. минимальная разность потенциалов на обкладках, при которой происходит электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы и размеров обкладок и от свойств диэлектрика. При практическом использовании конденсаторов для получения необходимой емкости собирают батареи из отдельных элементов, соединяя их последовательно или параллельно. При последовательном соединении конденсаторов заряд на обкладках остается величиной постоянной: Тогда электроемкость:
При последовательном соединении на каждый из конденсаторов приходится лишь часть разности потенциалов Δφ напряжения источника, вследствие чего уменьшается возможность пробоя конденсаторов. При параллельном соединении конденсаторов напряжение остается величиной постоянной: Тогда общая электроемкость:
Пробивное напряжение такой батареи равно пробивному напряжению того из конденсаторов, у которого оно наименьшее.
Использование моста Сотти для экспериментального определения емкости конденсатора и вывод рабочей формулы
В данной работе емкость измеряется при помощи мостовой схемы – моста Сотти (рис. 1).
Если источник тока включен, то в цепи, в том числе и на участке При равновесии моста потенциалы точек
По аналогичным соображениям:
Токи в ветвях
Сопротивление участка цепи переменного тока, содержащего конденсатор, определяется по формуле
где К однородным участкам цепи АЕ, ЕВ, АD и DВприменим закон Ома в виде:
тогда равенства (6) и (7) примут вид:
Разделив почленно равенство (9) на (10), учитывая при этом равенства (4), (5) и (8) получим:
Поскольку сопротивления плеч потенциометра
где
Порядок выполнения работы
1. Собрать цепь по схеме, изображенной на рис. 1, подключив конденсатор неизвестной электроёмкости 2. Включить источник питания и осциллограф, дождаться появления на экране осциллографа синусоиды. 3. На магазине емкостей установить значение емкости 0,5мкФ. С помощью движка реостата добиться на экране осциллографа прямой линии. Внести значения 4. По формуле (12) вычислить 5. Повторить пункты 1-4 для 6. Повторить п. 1-5 для конденсатора неизвестной электроёмкости 7. Рассчитать средние значения неизвестных емкостей, абсолютную и относительную погрешности измерений и занести в таблицу 1. 8. Соединить измеренные конденсаторы 9. Рассчитать по формуле (12)
10. Найти общую электроемкость при последовательном соединении 11. Оценить относительную погрешность:
12. Соединить измеренные конденсаторы 13. Рассчитать по формуле (12) 14. Найти общую электроемкость 15. Оценить относительную погрешность по формуле (13)
Таблица 1.
Таблица 2.
Контрольные вопросы
1. Что называется электроемкостью уединенного проводника? От чего она зависит? 2. В каких единицах измеряется электроемкость? 3. Что представляет собой конденсатор? 4. Опишите устройство и принцип действия моста Сотти. 5. Три одинаковых конденсатора один раз соединены последовательно, другой – параллельно. Во сколько раз и когда электроемкость батареи будет больше? 6. Написать формулу электроемкости плоского конденсатора. 7. Как определить общую электроемкость при параллельном и последовательном соединении? 8. Какой радиус должен иметь проводящий шар, чтобы в вакууме его емкость равнялась 1 Ф? 10. Можно ли, имея два одинаковых конденсатора, получить емкость вдвое меньшую и вдвое большую, чем у одного из них? Если можно, то, как это сделать?
Рекомендуемая литература
1. Трофимова Т. И. Курс физики.- М.: Высш. шк., 2004 2. Электростатика. Постоянный электрический ток: учеб. пособие. /B.C. Кунаков, И.В. Мардасова, О.М. Холодова, В.А. Тызыхян. – Ростов н/Д: Издательский центр ДГТУ, 2010. – 66 с. 3. Яворский Б. М., Детлаф А. А. Справочник по физике.-М.:Наука, 2006 4. Калашников С.Г. 6-е изд., стереот. - М.: ФИЗМАТЛИТ, 2003.- 624 с.
Редактор А.А.Литвинова В печать Объём 0,7 усл.п.л. Офсет. Формат 60х84/16. Бумага тип №3. Заказ № . Тираж 50 экз . Цена Издательский центр ДГТУ Адрес университета и полиграфического предприятия: 344010, г.Ростов-на-Дону, пл.Гагарина,1. |



 , то потенциал проводника примет некоторое значение
, то потенциал проводника примет некоторое значение  , причем
, причем  , т.е.
, т.е.  . Следовательно,
. Следовательно, -
- конденсатора понимается физическая величина, равная отношению заряда
конденсатора понимается физическая величина, равная отношению заряда 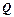 , накопленного в конденсаторе, к разности потенциалов (
, накопленного в конденсаторе, к разности потенциалов (  ) между его обкладками:
) между его обкладками:
 , (1)
, (1) =8,85·10–12 Ф/м – электрическая постоянная;
=8,85·10–12 Ф/м – электрическая постоянная;  – диэлектрическая проницаемость среды, заполняющей пространство между обкладками;
– диэлектрическая проницаемость среды, заполняющей пространство между обкладками;  – расстояние между пластинами,
– расстояние между пластинами,  - площадь обкладок.
- площадь обкладок. , напряжения суммируются:
, напряжения суммируются: 
 . (2)
. (2) , заряд батареи конденсаторов:
, заряд батареи конденсаторов:  .
. . (3)
. (3)
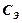 – магазин емкостей (эталонная емкость);
– магазин емкостей (эталонная емкость);  – конденсатор, емкость которого надо измерить; источник переменного тока (
– конденсатор, емкость которого надо измерить; источник переменного тока (  и
и  - плечи реохорда;
- плечи реохорда;  и
и  - сопротивления плеч
- сопротивления плеч  , течет ток, а на экране осциллографа видна синусоида. Подбором сопротивлений
, течет ток, а на экране осциллографа видна синусоида. Подбором сопротивлений  ) равна нулю (состояние равновесия моста), а на экране осциллографа синусоида сменяется горизонтальной прямой. После перехода через положение равновесия амплитуда синусоиды снова увеличивается.
) равна нулю (состояние равновесия моста), а на экране осциллографа синусоида сменяется горизонтальной прямой. После перехода через положение равновесия амплитуда синусоиды снова увеличивается. и
и  равны (
равны (  ). Это значит, что разность потенциалов на участке
). Это значит, что разность потенциалов на участке  по величине равна разности потенциалов на участке
по величине равна разности потенциалов на участке  :
: . (4)
. (4) . (5)
. (5) ,
,  будут равны по величине:
будут равны по величине: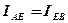 , (6)
, (6) . (7)
. (7) , (8)
, (8) – электроемкость конденсатора; ω – циклическая частота.
– электроемкость конденсатора; ω – циклическая частота. ,
, , (9)
, (9) . (10)
. (10)
 . (11)
. (11) и
и  пропорциональны их длине, условие равновесия запишется в виде:
пропорциональны их длине, условие равновесия запишется в виде: , (12)
, (12) - длина реохорда,
- длина реохорда,  .
. ,
,  ,
,  в таблицу 1.
в таблицу 1. . Результаты занести в таблицу 1.
. Результаты занести в таблицу 1. = 2,0; 4,0 мкФ. Записать значения
= 2,0; 4,0 мкФ. Записать значения  .
.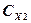 последовательно и повторить пункты 1-5. Записать значения
последовательно и повторить пункты 1-5. Записать значения 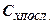 . Результаты занести в таблицу 2.
. Результаты занести в таблицу 2. по формуле (2) для средних значений
по формуле (2) для средних значений  (13)
(13) в таблицу 2.
в таблицу 2. . Результаты занести в таблицу 2.
. Результаты занести в таблицу 2. при параллельном соединении по формуле (3) для средних значений
при параллельном соединении по формуле (3) для средних значений 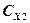 .
.