 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Профиль скорости при Профиль скорости при 12
Ламинарном движении. турбулентном движении
Итак, кинетическая энергия ламинарного потока вдвое больше кинетической энергии, подсчитанной по средней скорости. Если же эпюра скоростей в сечении близка к прямоугольной, т.е. скорости в разных точках сечения примерно равны средней скорости, как при турбулентном движении, то коэффициент Кориолиса a близок к 1. На основе обработки многочисленных данных, полученных при испытаниях на реках и каналах, установлено, что для больших открытых потоков a=1,1. Это безнапорное движение. При напорном (когда нет свободной поверхности жидкости) турбулентном движении жидкости в трубах коэффициент Кориолиса a=1+2,65l , где l - коэффициент гидравлического трения (Дарси); Vmax/Vср=1+1,3 В наших опытах движение турбулентное (a » 1), поэтому в расчетах его не учитываем. Итак, Учитывая уравнение неразрывности потока Q=V1w1= Vсwс получим формулу, справедливую для всех дроссельных расходомеров: где m - коэффициент расхода дроссельногоприбора; С- коэффициент дроссельного прибора. Теоретически вычислить значение коэффициентов m и С затруднительно. Они зависят не только от геометрических характеристик, но и от числа Рейнольдса и определяются опытным путем.
К дроссельным приборам, применяющимся для измерения установившихся расходов жидкостей, в т. ч. и газов, относятся: 1) РАСХОДОМЕРНАЯ ДИАФРАГМА. ( см. рис.2) 2) РАСХОДОМЕРНОЕ СОПЛО. (см. рис.3) 3) РАСХОДОМЕРНАЯ ТРУБА. ( Труба Вентури. см рис. 4 ) Для диафрагм и сопл значения m взяты из экспериментальных данных в зависимости от m=d/D (где d- диаметр сопла или диафрагмы; D- диаметр трубы) и от числа Рейнольдса Re. При Re > 105, m уже не зависит от Re (квадратичная зона сопротивления),а зависит только от отношения площадей(см. табл. 1).
Таблица 1-Коэффициенты расхода m
Расходомерная труба (труба Вентури) представляет собой вставку в основную трубу диаметром D трубы меньшего диаметра d, которая соединена с основной коническими переходами. В основной трубе и в суженном сечении присоединены пьезометры, по разнице показаний которых можно определить расход Q. Для трубы Вентури, показанной на рисунке 4, значение m практически совпадает со значением для сопл. Для трубы с коническим входом (двухконусного расходомера) m » 0,96 - 0,98. Итак, дроссельные приборы основаны на зависимости, устанавливающейся по уравнению Бернулли в потоке жидкости между расходом и искусственно создаваемым в 2-х сечениях перепадом давления.
РАСХОДОМЕРНАЯ ДИАФРАГМА
В данной работе необходимо измерить расход с помощью расходомерной диафрагмы. Рассмотрим поток жидкости, проходящий через отверстие диафрагмы (см. рис. 5) Его можно рассматривать как внезапное сжатие (происходящее на диафрагме, где жидкость, движущаяся по трубе диаметром D=20 мм, вынуждена проходить через отверстие с острой кромкой в диафрагме диаметром d=12 мм.) с последующим расширением потока после диафрагмы, когда площадь живого сечения потока на некотором расстоянии от диафрагмы снова становится равной площади сечения трубы. Сразу после прохождения отверстия в диафрагме площадь живого сечения потока wс будет меньше площади отверстия wотв из-за сжатия струи, характеризуемом коэффициентом сжатия: e=wс/wотв Наибольшую скорость поток будет иметь в сечении wс. Из-за возрастания скорости Vс в сжатом сечении (по уравнению неразрывности) увеличивается удельная кинетическая энергия потока, что по уравнению Бернулли вызывает соответствующее уменьшение удельной потенциальной энергии потока (падение давления в сечении с-с по сравнению с давлением в сечении 1-1). Таким образом, между сечениями 1-1 и с-с создается перепад давлений. Выбрав плоскость сравнения по оси потока, запишем уравнение Бернулли для сечений 1-1 и с-с. Учитывая, что z1= z2 и a1=aс » 1, получим
где x1-2 = xдиаф - коэффициент сопротивления отверстия диафрагмы. Из уравнения неразрывности Q=V1w1= Vсwс находим
Тогда из уравнения Бернулли Dh= Пренебрегая в первом приближении местными потерями на диафрагме (x диаф » 0), получим Dh= откуда выразим скорость в сжатом сечении
Тогда расход найдем как
Q = wс×Vс = wотв Vс =e×wотв
Обозначив через mт = mт будем называть теоретическим коэффициентом расхода. Разность (перепад) давлений замеряется двумя пьезометрами и расход определяется по формуле Q=Ст где Ст=mт×w mт и Ст отличаются от действительных значений mдейств и Сдейств, т.к. мы приняли a1=aс=1; x диаф » 0 ; e=0,64. Кроме того, на практике замер давлений производится в сечениях, не совпадающих с расчетными по уравнению Бернулли. Для турбулентного движения жидкости квадратичной зоны сопротивления Сдейств называется постоянной расходомера. В связи с вышеизложенным действительные значения коэффициентов mдейств и Сдейств определяют опытным путем. Для этого проводят опыт: измеряют Dh по разности показаний пьезометров; измеряют расход Qоб объемным способом. Подставляя в уравнение Qоб=Cдейств Дроссельные расходомеры широко применяют для измерения расходов различных жидкостей и газов. Однако все они обладают значительным гидравлическим сопротивлением (трубы Вентури-меньшим, диафрагмы-большим) и вызывают большие потери давления (напора) в измеряемом потоке. Кроме того, при больших расходах жидкости в самом узком сечении этих расходомеров часто возникает кавитация. В этом случае использование дроссельных расходомеров исключается. Для получения хорошей точности измерений перед расходомером должен быть прямой участок трубы достаточной длины.
12 |





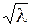 ; a » 1.
; a » 1.

 =mw
=mw  ,
,
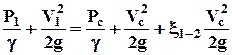

 =
=  +xдиаф×
+xдиаф×  ×
× 
 =wотв
=wотв 
 постоянную для данной диафрагмы величину, получим Q=mт wотв
постоянную для данной диафрагмы величину, получим Q=mт wотв  .
.
 -теоретический коэффициент дроссельного прибора.
-теоретический коэффициент дроссельного прибора.