 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Для элементарной струйки идеальной жидкости
По гидравлике ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
Ижевск 2007 Лабораторная работа № 6 «Исследование движения жидкости в трубе переменного Сечения» ( иллюстрация уравнения Бернулли) I. Цель работы: 1. Исследовать движения жидкости в трубе переменного сечения, зафиксировать изменения скоростей и давлений на участках трубы. 2. Определить скорости и скоростные напоры на участках опытным и теоретическим путем. 3. Построить графическое изображение уравнения Бернулли для исследуемой трубы. II. Описание опытной установки Лабораторная установка для исследования уравнения Бернулли и иллюстрации пьезометрической и напорной линии изображена на рисунке 1. Установка состоит из бака А, к которому присоединена горизонтальная труба В, состоящая из труб различных диаметров d1= 40,2 мм, d2 = 20 мм и d3 = 26,5 мм. Труба снабжена на выходе краном С, предназначенным для регулирования расхода жидкости. К трубе присоединены пьезометры 1, 2, 3, 4, 5, 6 и гидрометрические трубки 1′, 2′, 3′, 4′, 5′, 6′, расположенные на определенных расстояниях друг относительно друга. Бак заполняется водой из водонапорной трубы Е при закрытом кране С. При этом уровни жидкости во всех пьезометрах и гидрометрических трубках находятся на одинаковой высоте с уровнем жидкости в баке. Далее кран открывают и наблюдают положение уровней в пьезометрах и гидрометрических трубках при установившемся движении по трубе В (установившийся уровень жидкости в баке поддерживают открытием крана Е). При данном положении крана С определяют расход жидкости.
III. Порядок проведения работы: 1. Измерение расхода жидкости. Наиболее простым и вместе с тем точным методом измерения расхода жидкости является объемный способ. При объемном способе измеренияпротекающая в исследуемом потоке жидкость поступает в мерный бак. Мерный бак М (рисунок 1) состоит из открытого резервуара с водомерным стеклом. Уровень воды в нем соответствует уровню воды в баке. Рядом со стеклом нанесена шкала, по которой можно отсчитать количество воды поступившей в мерный бак за время опыта. Для определения расхода жидкости необходимо замерить объем поступившей жидкости и время заполнения. Для этого, записывают начальный уровень жидкости в баке. Включают секундомер, проводят опыт, в конце опыта записывают конечный уровень жидкости в баке, определяют увеличение уровня Δh см за время опыта t с. Определяют объем воды W поступившей в мерный бак W = Δh · S. Где S – площадь поперечного сечения бака равная в нашем случае 1500 см2.
Рисунок 1 – Схема лабораторной установки 1,2,3,4,5,6 – пьезометрические трубки; 1′,2′,3′4′,5′,6′ - гидрометрические трубки.
Тогда искомый расход жидкости находится из соотношения
Хотя объемный способ определения расхода является точным, однако при больших расходах жидкости этот способ не применяется, т. к. требует наличия весьма громоздких баков. Для измерения больших расходов на практике пользуются специальными приборами: водомер Вентури, водомерная шайба (диафрагма) и сопло. В данной лабораторной работе расход определяется объемным способом.
2. Порядок проведения и оформления работы Открывают вентиль С (рисунок 1), обеспечивая в трубе установившийся режим движения (это достигается путем открытия вентиля Е, с помощью которого заполняется резервуар А) и только после этого приступают к измерению расхода воды с помощью водомерного бака М и секундомера. Одновременно с этим записываются показания всех пьезометров и гидрометрических трубок. Данные заносят в таблицу 1. Затем увеличивают расход. (Это достигается путем большего открытия вентиля С). При этом следят, чтобы уровень воды в баке поддерживался постоянным и производят те же самые замеры, что и в первом опыте. Сделав еще один-два увеличения расхода, можно приступить к оформлению работы. Замеры и вычисления заносятся в таблицу 1. IV. К отчету прилагается: Оформление лабораторной работы заключается в записи основных формул, зарисовке соответствующей схемы установки, составлении таблицы с результатами испытаний и вычислений,
Таблица 1 – Результаты измерений и вычислений
построении графиков изменения полного и пьезометрического напоров вдоль трубы переменного сечения. График полного напора строится при помощи подсчитанных в таблице 1 средних скоростей в сечениях. При построении графиков берутся средние значения пьезометрических и гидрометрических напоров.
V. Обработка опытных данных: Для измерения малых пьезометрических напоров в сечениях 1, 2, 3 и т.д. к трубе присоединяют пьезометры. Высота поднятия воды в пьезометре h = Скоростной напор Гидрометрическая трубка или, как ее называют, трубка Пито, представляет собой согнутую под прямым углом трубку, открытый конец которой устанавливается против движения потока (см. рисунок 2). Трубкой Пито измеряется скорость течения в той точке, в которую помещен ее открытый конец. При этом в начальный момент трубка заполняется жидкостью и работает как обыкновенный пьезометр. Затем последующие частицы набегают со скоростью V на неподвижную жидкость в трубке, от этого их скорость падает практически до нуля, и они оказывают на неподвижную в трубке жидкость дополнительное давление, соответствующее их потерянной кинетической энергии
Рисунок 2 – Схема работы пьезометрической и гидрометрической трубок Выражение этого давленияможнополучить, пользуясь уравнением Бернулли. Принимая за ось сравнения горизонтальную прямую, совпадающую с осью открытого выступающего конца трубки, напишем уравнение Бернулли для открытого конца пьезометра вдали от трубки Пито и для ее выступающего конца, принимаяa1= a2= a
где Рп- гидродинамическое давление на месте установки трубки Пито; V1, P1 - соответственно скорость и давление вдали от нее в той же струйке, в невозмущенной части потока. Из последней формулы следует, что где hск - разность высот уровней в трубке Пито и пьезометре. Таким образом, hск =
где Vср1, Vср2 и т.д. - средние скорости в сечениях 1, 2, и т.д. ω1 , w2 и т.д. - площади живых сечений 1, 2, и т.д. потока жидкости; Q- расход жидкости через трубопровод, см3 / сек. На основании уравнения(1) средняя скорость в любом сечении трубы равна: Vср = Q = const и не зависит от выбора сечения. ω – площадь живого сечения потока, см2
Диаметр участков d1 = 4,02 см; d2 = 2,0 см; d3 = 2,65 см.
VI. Материалы к работе: Фундаментальным уравнением, устанавливающим зависимость между средней скоростью движения жидкости, гидродинамическим давлением в ней и высотной отметкой центра тяжести, является уравнение Бернулли. Это уравнение справедливо только для установившегося движения. Если скорость в каждой точке данного поперечного сечения потока жидкости с течением времени остается неизменной по величине и направлению, а также давление в данной точке с течением времени остается постоянным, то такое движение называется УСТАНОВИВШИМСЯ. Следовательно, чтобы получить установившееся течение в трубе, необходимо поддерживать в ней постоянный напор (Н=соnst), т. е. уровень воды в напорном баке не должен изменяться.. Уравнение Бернулли записывается относительно плоскости сравнения, которая обязательно должна быть горизонтальной. Для элементарной струйки идеальной жидкости уравнение Бернулли можно представить в следующем виде:
где z - геометрическая высота , м; P/γ - приведенная пьезометрическая высота (если Р - абсолютное давление) или пьезометрическая высота (если Р - избыточное давление), м; V2/2g - скоростной напор, м.
Сумма геометрической и пьезометрической высот называется пьезометрическим напором. Все слагаемые в уравнении Бернулли измеряются единицами длины. Действительно, величиной z измеряется вертикальная координата центра тяжести сечения трубки (см. рисунок 3), размерность В соответствии с этим, уравнение Бернулли можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полный напор, т. е. сумма пьезометрического и скоростного напоров есть величина постоянная по всем сечениям струйки. В то же время члены, входящие в уравнение Бернулли, являются мерами удельной потенциальной и удельной кинетической энергий движущейся жидкости.
Рисунок 3 – Графическое изображение уравнения Бернулли для элементарной струйки идеальной жидкости
Частица жидкости, имеющая массуm , весом mg , расположенная на высоте zотносительно некоторой плоскости, способна совершить работу, т.е. ее потенциальная энергия относительно плоскости равна mgz. Эта потенциальная энергия (относительно плоскости), будучи поделена на вес частицы, дает величинуmgz/mg = z, которая называется удельной потенциальной энергией положения.
Для получения физического представления о том, что величиной P/ g также измеряется потенциальная энергия, рассмотрим следующую схему : пусть к трубе Б, заполненной жидкостью с избыточным давлением Р (рисунок 4), присоединен пьезометр, снабженный краном при входе в него. До открытия крана частица жидкости весом mg находится под давлением Р.
Рисунок 4 – Схема работы пьезометра
После открытия крана частица жидкости поднимается на высоту h, т.е. потенциальная энергия единицы веса жидкости увеличивается на величину h, в то же время высота жидкости в пьезометре: h = следовательно, удельная потенциальная энергия увеличится на величину
Удельная кинетическая энергия, т.е. энергия, отнесенная к единице веса, будет равна:
Следовательно, напор определяет энергию, отнесенную к единице веса жидкости или так называемуюполную удельную энергию жидкости. Отсюда следует, что в случае идеальной жидкости уравнение Бернулли представляет собой закон сохранения механической энергии, составленный применительно к единице веса жидкости. Напоры измеряются линейными величинами. Это дает возможность строить графики уравнения Бернулли. По оси абсцисс откладывается расстояние между сечениями струйки от некоторого сечения, принимаемого за начальное, начальным сечением является какое-то крайнее сечение, а от него в выбранном масштабе откладывается расстояние между сечениями (рисунок 3: 1-е сеч.,2-е сеч., 3-е сеч., ... n-е сеч.), а по оси ординат - значения составляющих напора для всех сечений струйки. Подобная графическая иллюстрация уравнения Бернулли изображена на рисунке 3. Так как сумма трех членов располагаются на одинаковых вертикальных расстояниях от плоскости сравнения. Линия, проходящая через точки В1, В2, В3, называется напорной линией (для идеальной жидкости она параллельна плоскости сравнения, т.е. горизонтальна). Линия, проходящая через точки а1, а2, а3, называется пьезометрической линией. Она показывает изменение удельной потенциальной энергии по длине струйки. В данной лабораторной работе необходимо построить линии пьезометрического и полного напоров. При постановке опыта мы будем иметь дело с реальной жидкостью, в которой, при ее движении возникают касательные напряжения. В этом случае уравнение Бернулли должно существенным образом измениться. Для реальной жидкости полная удельная энергия или напор Н будет убывать по направлению движения. Причина этого - затрата энергии на преодоление сопротивления движению, обусловленного внутренним трением, возникающим из-за вязкости реальной жидкости. Тогда уравнение Бернулли приобретает вид:
где - h1-2 - потери напора между сечениями 1 и 2; a - коэффициент неравномерности распределения скоростей по сечению потока. Для ламинарного теченияa = 2, для турбулентного режима движения среднее значение a = 1,1. V1 , V2 - средние скорости в сечениях 1 и 2.
ЛАМИНАРНЫЙ режим движения - это режим, при котором поток жидкости движется отдельными струйками или слоями, причем траектории движения отдельных частиц между собой не пересекаются. (Re < 2320) ТУРБУЛЕНТНЫЙ режим движения характеризуется беспорядочностью движения частиц, причем частицы жидкости сталкиваются между собой, в результате чего теряется больше энергии, чем при ламинарном движении. (Re > 2320)
|




 , см3/с
, см3/с




 и дает пьезометрический напор, (плоскость сравнения совмещаем с осью трубы, поэтому z= 0). При больших пьезометрических напорах к сечениям отбора давления 1, 2, 3 и т.д. присоединяют обычно манометры.
и дает пьезометрический напор, (плоскость сравнения совмещаем с осью трубы, поэтому z= 0). При больших пьезометрических напорах к сечениям отбора давления 1, 2, 3 и т.д. присоединяют обычно манометры. можно измерить с помощью гидрометрических трубок, поставленных в каждом сечении, или вычислить по средней скорости Vср.
можно измерить с помощью гидрометрических трубок, поставленных в каждом сечении, или вычислить по средней скорости Vср.

 ; т. к. V=0,то
; т. к. V=0,то  =
=  +
+ 
 ,
, . Как отмечалось выше, скоростные напоры
. Как отмечалось выше, скоростные напоры  могут вычисляться еще и по средним скоростямVср. При установившемся режиме движения жидкости в трубке, в каждом ее сечении расход будет постоянным, т.е.
могут вычисляться еще и по средним скоростямVср. При установившемся режиме движения жидкости в трубке, в каждом ее сечении расход будет постоянным, т.е. (1)
(1) (2)
(2)
 (3)
(3)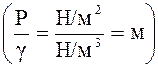 , размерность величины
, размерность величины 




 (4)
(4) , м
, м (5)
(5)