 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Решение задачи аппроксимации с использованием математических пакетов
Вопросы, подлежащие изучению
1.Постановка задачи аппроксимации. 2.Основные понятия: базисные функции, матрица Грама, система нормальных уравнений, критерий аппроксимации. 3.Матрица Грама для степенного базиса. 4.Правило построения системы нормальных уравнений и число уравнений в системе. 5.Алгоритм получения коэффициентов линейных и квадратичных аппроксимирующих функций. 6.Графическая иллюстрация метода МНК. 7.Формулы оценки качества аппроксимации для линейной и квадратичной функции.
Задание 1. Выбрать индивидуальное заданиеиз табл. 6.7-1 и табл. 6.7-2 для решения задачи аппроксимации методом наименьших квадратов: · аппроксимируемую функцию f1 или f2 из табл. 6.7-1, заданную в предписанных узлах (при «ручном расчете» 4 точки); · значения функции f1 или f2из табл. 6.7-2 в предписанных узлах. 2. Выполнить линейную и квадратичную аппроксимацию: · составить систему нормальных уравнений и решить её; · вычислить значения аппроксимирующих функций в узловых точках и сравнить их со значениями исходной функции; · оценить погрешность. 3. Построить график заданной функции (по множеству точек) и отобразить на графике зависимости, полученные МНК. Получить решения с помощью математических пакетов.
Варианты задания
Таблица 6.7-1
Таблица 6.7-2
Содержание отчета
1.Индивидуальное задание. 2.Линейная и квадратичная аппроксимация: · значения элементов матрицы Грама и столбцов свободных членов, представленные в табл. 6.7-3: Таблица 6.7-3
· системы нормальных уравнений и их решения, аппроксимирующие функции; · исходная функция и результаты аппроксимации Таблица 6.7-4
· оценка погрешности (среднеквадратическое отклонение). 3.Графики исходной аппроксимируемой функции 4.Результаты аппроксимации, полученные с помощью математического пакета.
Пример выполнения задания
Задание для решения задачи аппроксимации Для решения задачи аппроксимации методом наименьших квадратов выберем функцию y(x), заданную следующей таблицей:
2. Линейная и квадратичная аппроксимация: · Вычислить и записать в табл. 6.7-3 элементы матрицы Грама и столбец свободных членов:
· составить системы нормальных уравнений: для линейной функции
· решить систему уравнений: получим коэффициенты C0=5.744 и C1=-0.442, тогда Для квадратичной функции
решая систему, получим коэффициенты C0=22.507, C1=-9.299 и С3=0.974, тогда
· вычислить значения аппроксимирующих функций в узловых точках и занести эти значения в табл. 6.7-4:
· оценить погрешность (среднеквадратическое отклонение): - для линейной аппроксимации - для квадратичной аппроксимации Приведенные расчеты показали, что для рассматриваемой функции предпочтительнее квадратичная аппроксимация, т.к. 3. Графики заданной
Решение задачи аппроксимации с использованием математических пакетов При использовании пакетаMathcad для решения задачи аппроксимации используется функция linfit(X, Y, x), позволяющая определить коэффициенты, аппроксимирующей функции. Аппроксимируемая функция задается в виде матриц-столбцов (Х – аргументы, Y – значения функции). Вспомогательная функция f(x) - определяет порядок аппроксимирующего многочлена. Матрица S содержит полученные значения коэффициентов аппроксимирующего многочлена. Ниже приведены расчеты и графические иллюстрации аппроксимации таблично заданной функции многочленом 1-й, 2-й и 3-й степени, а также вычислены соответствующие погрешности по методу наименьших квадратов:
При использовании пакета MatLabдля решения задачи аппроксимации используется функция p=polyfit(x,y,n), где x,y – соответственно векторы значений аргументов и функции, n – порядок аппроксимирующего полинома, а p – полученный в результате вектор коэффициентов аппроксимирующего полинома длинной n+1.
6.7.4. Контрольные вопросы по теме Аппроксимация функций
1. Что называется аппроксимацией функций? 2. Как называется функция, приближенно описывающая таблично заданную функцию? 3. Как называется полином, построенный по таблично заданной функции и обеспечивающий полное совпадение в используемых для его построения точках? 4. Какое минимальное количество узлов нужно для построения аппроксимирующего многочлена 2-й степени? 5. Каким полиномом проводится аппроксимация, если система нормальных уравнений содержит два уравнения? 6. Каким полиномом проводится аппроксимация, если система нормальных уравнений содержит три уравнения? 7. Для чего предназначен метод наименьших квадратов? 8. Как изменяется точность описания исходной функции аппроксимирующим многочленом, если увеличить число табличных значений функции? 9. Что служит критерием близости аппроксимируемой и аппроксимирующей функций при использовании метода наименьших квадратов? 10. Что показывает критерий аппроксимации? 11. Какой термин используется при решении задачи аппроксимации? 12. Можно ли аппроксимировать функцию, заданную таблицей из 20 точек, многочленом 2-й степени? 13. Из какого условия в методе наименьших квадратов определяются параметры аппроксимирующей функции? 14. Что происходит с точностью аппроксимации с увеличением количества узлов аппроксимации? 15. Когда используется метод наименьших квадратов для построения аппроксимирующей функции? 16. Что служит мерой погрешности аппроксимации в точке? 17. Как называется матрица системы нормальных уравнений? 18. Как выбирается степень аппроксимирующего полинома (m) в методе наименьших квадратов в соответствии с количеством узлов таблично заданной функции- (n)? 19. Чем являются элементы матрицы Грама? 20. Когда система нормальных уравнений имеет единственное решение?
|








 -номер узла
-номер узла

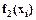



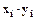




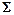
 и
и  в узловых точках, представленные в табл. 6.7-4:
в узловых точках, представленные в табл. 6.7-4:


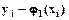

 (
(  ) и аппроксимирующих функций
) и аппроксимирующих функций 
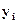







 система нормальных уравнений примет вид (линейная аппроксимация):
система нормальных уравнений примет вид (линейная аппроксимация): .
. .
. система нормальных уравнений примет вид (квадратичная аппроксимация):
система нормальных уравнений примет вид (квадратичная аппроксимация):
 .
.
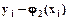
 ,
,
 .
.

 Пример ЛР-6-7
Пример ЛР-6-7 >> plot(X,Y,'ko',t,gg2,'k-');
>> plot(X,Y,'ko',t,gg2,'k-');  >> plot(X,Y,'ko',t,gg3,'k-');
>> plot(X,Y,'ko',t,gg3,'k-'); 