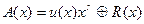ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Код Хэмминга для исправления одиночных ошибок и обнаружения двойных ошибок

Для получения кода с дополнительным обнаружением двойных ошибок из кода с исправлением одиночных ошибок, добавим еще одну проверку на четность (и еще одну позицию), охватив этой проверкой все сообщение.

Если произойдет одиночная ошибка, то ее выявит проверка на четность всего слова, а место ошибки определится анализом четности количества единиц в подмножествах. При искажениях содержимого двух разрядов общая проверка на четность ошибку не зафиксирует, но проверка в соответствии с таблицей 2 укажет, что ошибка есть, хотя определить ее место становится уже невозможным.

Коды, исправляющие ошибки, иногда используются при передаче данных, например в случае симплексного канала, в котором нельзя запросить повторную передачу. Однако чаще более эффективным оказывается обнаружение ошибки с последующей повторной передачей.

Циклические коды

Циклические коды (CRC - Cyclic Redundance Code) – это семейство помехоустойчивых кодов, включающее в себя в качестве одной из разновидностей коды Хэмминга. В целом оно обеспечивает большую гибкость с точки зрения возможности реализации кодов с необходимой способностью обнаружения и исправления ошибок, определяемой параметром d0, по сравнению с кодами Хэмминга (для которых d0=3 или d0=4). Широкое использование циклических кодов на практике обусловлено также простотой реализации соответствующих кодеров и декодеров.

Основные свойства и название циклических кодов связаны с тем, что все разрешенные комбинации бит в передаваемом сообщении (кодовые слова) могут быть получены путем операции циклического сдвига некоторого исходного кодового слова:

Циклические коды задаются с помощью так называемых порождающих полиномов (многочленов) или их корней. Порождающий полином имеет вид

где .

Кроме того, вводятся полином исходного сообщения:

и кодированного сообщения

Для этих полиномов, представляющих собой по существу альтернативную запись чисел в двоичной системе счисления, определяются операции сложения, умножения и деления, необходимые для организации кодирования и декодирования сообщения. Все операции выполняются по модулю 2.

Рассмотрим последовательность кодирования на примере циклического кода (7,4,3), имеющего . Код характеризуется тройкой чисел , где – общее число разрядов в передаваемом сообщении, включая проверочные ( ), – число информационных разрядов, – минимальное кодовое расстояние между разрешенными кодовыми комбинациями, определяемое как минимальное число различающихся бит в этих комбинациях.

1) информационная часть сообщения записывается в виде полинома:

В рассматриваемом примере =4 и для сообщения 0111 получается

2) умножается , что соответствует циклическому сдвигу исходного сообщения на разрядов влево:

3) полученный многочлен делится на :

где – полином-частное с максимальной степенью ;

– полином-остаток с максимальной степенью ;

– обозначение поразрядной операции суммирования по модулю 2 (исключающее ИЛИ). Кодированное сообщение представляется в виде

Таким образом, в этом случае

Передаваемое кодированное сообщение в обычной двоичной форме имеет вид:


↔	↔
– бит	– бит

Три порождающих многочлена стали международными стандартами:

CRC-12 = x12 + x11 +x3 + x2 + x1 + 1;

CRC-16 = x16 + x15 + x2 + 1;

CRC-CCITT = x16 + x12 + x5 + 1.

Все три многочлена делятся на x + 1. CRC-12 используется для символов длиной в 6 бит. Остальные применяются для 8-битовых символов. 16-битовые контрольные суммы, такие как CRC-16 и CRC-CCITT, обнаруживают все одинарные и двойные ошибки, все ошибки с нечетным количеством бит, все пакеты ошибок длиной не более 16 бит, 99,997 процента 17-битовых пакетов ошибок и 99,998 процента пакетов ошибок длиной в 18 и более бит.

Порядок выполнения работы

1. Ознакомиться с теоретической частью к лабораторной работе.

2. Представить алгоритмы, по которым происходит кодирование передаваемого сообщения с использованием кодов представленных в 1.2… 1.5 на передающей стороне.

3. Представить алгоритмы, по которым происходит декодирование принимаемого сообщения с использованием кодов представленных в 1.2…1.5 на приемной стороне.

4. Написать программу по пункту 2 для передаваемого сообщения (приложение А) с использованием алфавита кода КОИ-7 (приложение Б).

5. Написать программу по пункту 3 для принимаемого сообщения (приложение А) с использованием алфавита кода КОИ-7 (приложение Б).

6. Исследовать канал передачи сообщения при наличии одной ошибки в передаваемом сообщении (приложение В) с использованием кодов представленных в пунктах 1.2… 1.5.

7. Исследовать канал передачи сообщения при наличии двух ошибок в передаваемом сообщении (приложение В) с использованием кодов представленных в 1.2… 1.5.

8. Исследовать канал передачи сообщения при наличии трех ошибок в передаваемом сообщении (приложение В) с использованием кодов представленных в 1.2… 1.5.

9. Представить отчет.

Примечание - Для циклического кода использовать порождающий полином

Требования к отчету

Отчет по лабораторной работе должен содержать:

а) Ф.И.О. и номер группы студента, номер и название работы, цель.

б) Алгоритмы* кодирования передаваемого сообщения с использованием кода проверки на четность, кода Хэмминга для исправления одиночных ошибок, кода Хемминга для исправления одиночных ошибок и обнаружения двойных, а так же циклических кодов.

в) Алгоритмы декодирования принимаемого сообщения с использованием кода проверки на четность, кода Хэмминга для исправления одиночных ошибок, кода Хемминга для исправления одиночных ошибок и обнаружения двойных, а так же циклических кодов.

г) Переданное сообщение.

д) Результаты приема сообщения на приемной стороне с использованием кода проверки на четность, кода Хэмминга для исправления одиночных ошибок, кода Хемминга для исправления одиночных ошибок и обнаружения двойных, а так же циклических кодов при наличии в сообщении одной ошибки.

е) Результаты приема сообщения на приемной стороне с использованием кода проверки на четность, кода Хэмминга для исправления одиночных ошибок, кода Хемминга для исправления одиночных ошибок и обнаружения двойных, а так же циклических кодов при наличии в сообщении двух ошибок.

ж) Результаты приема сообщения на приемной стороне с использованием кода проверки на четность, кода Хэмминга для исправления одиночных ошибок, кода Хемминга для исправления одиночных ошибок и обнаружения двойных, а так же циклических кодов при наличии в сообщении трех ошибок.

з) Выводы по пунктам д) е) и ж).

Примечание – Алгоритм (последовательность действий, направленных на получение определённого результата за конечное число шагов) это, не в коем случае, не листинг (текст компьютерной программы или её части, записанный на каком-либо языке программирования, обычно — на бумаге).

5 Контрольные вопросы

1. Дайте определение корректирующего кода.

2. Что понимают под кодовым расстоянием корректирующего кода.

3. Приведите алгоритм кодирования/декодирования передаваемой/принимаемой информации при использовании кода с проверкой на четность.

4. Приведите алгоритм кодирования/декодирования передаваемой/принимаемой информации при использовании кода Хэмминга для исправления одиночных ошибок.

5. Приведите алгоритм кодирования/декодирования передаваемой/принимаемой информации при использовании кода Хэмминга для исправления одиночных ошибок и обнаружения двойных.

6. Приведите алгоритм кодирования/декодирования передаваемой/принимаемой информации при использовании циклических кодов.

ПРИЛОЖЕНИЕ Б

Таблица 1 - код КОИ-7 (сокращенный) /3/

Восьмеричный код	Знак	Восьмеричный код	Знак	Восьмеричный код	Знак	Восьмеричный код	Знак
	Пробел		:		Q		Л
	!		;		R		М
	«		<		S		Н
	‘		=		T		О
	(		>		U		П
	)		?		V		Я
	*		A		W		Р
	+		B		X		С
	,		C		Y		Т
	-		D		Z		У
	.		E		Ю		Ж
	/		F		А		В
			G		Б		Ь
			H		Ц		Ы
			I		Д		З
			J		Е		Ш
			K		Ф		Э
			L		Г		Щ
			M		Х		Ч
			N		И
			O		Й
			P		К

Примечание - Код КОИ-7 в существенной степени совпадает с кодом ASCII, за исключением кодов строчных латинских букв, которые используются для прописных букв русского алфавита.