 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Порядок выполнения работы.
Лабораторная работа № 12. Тема: «Исследование резонанса напряжений в электрических цепях». Цель: Исследование резонанса напряжений: снять резонансные кривые при переменной ёмкости, определить на опыте соотношения между сопротивлениями отдельных участков и падениями напряжения на них, между активными и реактивными мощностями. Снять резонансные кривые при переменной ёмкости.
Приборы и оборудование: 1. Источник питания 2. Вольтметр 3. Амперметры 4. Блок конденсаторов 5. Катушка индуктивности 6. Резистор 7. Провода
Сведения из теории. Резонансом напряжений называют такой режим работы неразветвлённой электрической цепи, содержащий участки с индуктивностью и ёмкостью, при котором разность фаз напряжения на зажимах цепи и тока на входе цепи равна нулю. При этом сопротивления на реактивных участках равны между собой: 2πfL=1/2πfC=Zв, где Zв= Резонанс можно получить изменением частоты, индуктивности или ёмкости. При резонансе напряжений сила тока в цепи максимальная, что позволяет на опыте фиксировать точку резонанса по показаниям амперметра. Падения напряжения на реактивных участках равны между собой: UL=I*XL=I*XC=UC, кроме того UL=U(XL / R) и UC=U(XC /R), т.е. они будут больше напряжения на зажимах цепи, если XL=XC>R. Векторы напряжений UL и UC сдвинуты относительно друг друга на угол 1800, поэтому взаимно компенсируются при сложении: U= Полная мощность будет иметь активный характер: S=U*I= Форма резонансных кривых в значительной степени зависит от соотношения активного и волнового сопротивлений в цепи. Это соотношение учитывается добротностью контура: Q = Чем больше добротность, тем более острую форму будут иметь кривые тока, напряжений и мощностей.
Из анализа этой формулы следует, что резонанса можно добиться, изменяя частоту генератора, индуктивность катушки, ёмкость конденсатора или активные сопротивления. При резонансе токов: BL=BC; IL=IC; IL-IC=0; I=IQ1+IQ2, т.е. ток чисто активный и, следовательно, совпадает по фазе с напряжением на зажимах цепи (φ=0). Кроме того, он минимален, так как отсутствуют реактивные токи. Если BL>G1, a BC>G2, то IL>IQ1 и XC>IQ2, тогда возможен случай, при котором: I1>I=IQ1+IQ2, I2>I, т.е. сила токов в отдельных ветвях может оказаться больше, чем сила тока на входе цепи. Активная мощность в ветвях: P1=IQ1*U= P2=IQ2*U= S= т.е. полная мощность цепи равна активной. Это означает, что генератор снабжает цепь энергией, превращающейся в теплоту в активном сопротивлении катушки и конденсатора. Добротность контура Q=IL / I=IC / I=YB / Q , где YB=BL=BC – волновая проводимость цепи; IL и IC – реактивные токи при резонансе. Чем меньше активные сопротивление цепи, тем меньше потери энергии в ней и тем больше добротность контура.
Порядок выполнения работы. 1. Ознакомится с приборами, необходимыми для работы. Собрать схему согласно рисунку 1показать её преподавателю и объяснить принцип и особенности работы.
Рисунок 1
2. Установить в цепи по максимуму тока резонансный режим работы. Изменением величины ёмкости конденсатора добиться равенства индуктивного и ёмкостного сопротивлений. 3. Вычислить значение индуктивности катушки по результатам опыта, приняв Rк=18 Ом. 4. Измерить напряжение на элементах схемы и ток в цепи. Значения записать в таблицу 1. 5. Установить значение ёмкости больше, чем С0, затем меньше С0, снять значение напряжений на элементах цепи и записать их в таблицу 1. 6. Построить по результатам опыта векторные диаграммы для всех трёх режимов работы электрической цепи. 7. Определить кратность превышения индуктивного или ёмкостного напряжения над напряжением на входе цепи при резонансе, т.е. добротность: Q= Таблица 1.
8. Рассчитать частотные характеристики и изобразить их графики: XL=f(ω), XL=f(ω), Z=f(ω), I=f(ω), φ=f(ω). Результаты расчёта занести в таблицу 2. Таблица 2.
9. Определить полосу пропускания контура, проведя линию на высоте отношения I / / I0=1 / L= P=U*I*cosφ; S=
10. Сделать заключение относительно: а) возможности получения резонанса путём изменения ёмкости цепи; б) характера изменения резонансных кривых. Выводы записать в отчёт.
Контрольные вопросы: 1. Что называют резонансом напряжений? 2. Каким образом можно достичь резонанса напряжений? 3. Каковы характерные особенности сопротивлений цепи при резонансе напряжений? 4. Какую величину имеет коэффициент мощности и угол φ при резонансе напряжений? 5. Каким образом можно определить на опыте состояние резонанса напряжений? 6. Каковы особенности падений напряжений на отдельных участках исследуемой цепи при резонансе напряжений? 7. Что называют добротностью контура? 8. Что называют резонансом токов? 9. Каким образом можно достичь резонанса токов? 10. Каковы характерные особенности проводимости цепи при резонансе токов? 11. Каким образом можно определить на опыте и зафиксировать резонанс токов? 12. Какова особенность токов в ветвях при резонансе токов? |



 – волновое сопротивление.
– волновое сопротивление. =Ua.
=Ua. =р.
=р. =
=  .
. =U2*G1;
=U2*G1; =U2*G2.
=U2*G2. =P1+P2,
=P1+P2,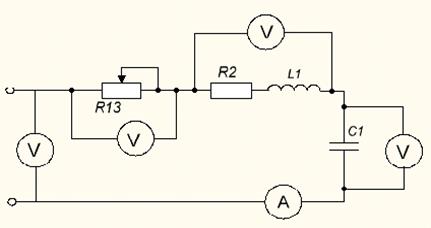
 .
.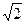 на резонансной кривой. Формулы для расчёта:
на резонансной кривой. Формулы для расчёта: ; XL=ω*L; XC=
; XL=ω*L; XC=  ; QC=UC*I; QL=UL*I;
; QC=UC*I; QL=UL*I; ; I=
; I=  ; sinφ=
; sinφ=  ; Q=QL-QC;
; Q=QL-QC; .
.