 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Построение диаграммы плавкости двухкомпонентной системы
ФИЗИКО-ХИМИЧЕСКИЙ АНАЛИЗ. ПОСТРОЕНИЕ ДИАГРАММЫ ПЛАВКОСТИ ДВУХКОМПОНЕНТНОЙ СИСТЕМЫ Методические указания к лабораторной работе № 10
Самара 2010
Составители: Ю.П. КОВРИГА, В.В. СЛЕПУШКИН, Б.М. СТИФАТОВ
УДК 541.123.2
Физико-химический анализ. Построение диаграммы плавкости двухкомпонентной системы:Метод. указ. к лаб. занятиям и задания для самостоятельной работыстудентов / Сам. гос. техн. ун-т; Сост. Ю. П. Ковригаа, В.В. Слепушкин, Б.М. Стифатов. Самара, 2010. 16с.
Кратко рассмотрены теоретические основы физико-химического анализа, построения диаграммы состояния двухкомпонентной системы по результатам термического анализа, даны задания для самостоятельной подготовки студентов. Методические указания рассчитаны на студентов специальностей химико-технологического, инженерно-технологического, физико-технологическо-го факультетов.
Табл. 4. Ил. 4. Библиогр. 5 назв.
Печатается по решению редакционно-издательского совета СамГТУ ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ФИЗИКО-ХИМИЧЕСКОГО АНАЛИЗА
В гетерогенных системах возможны переходы вещества из одной фазы в другую путем испарения, плавления, растворения твердых веществ, перераспределения растворенного вещества между двумя растворителями, кристаллизации и др. Равновесие в гетерогенной системе достигается при равенстве химических потенциалов каждого компонента во всех фазах системы. К основным понятиям фазового равновесия относятся: система, фаза, составная часть системы, компонент, число степеней свободы (вариантность). Система представляет собой тело или группу тел, находящихся во взаимодействии и мысленно или реально обособляемых от окружающей среды. Фазой называют однородную часть системы с одинаковыми физико-химическими и термодинамическими свойствами, отделенную от других частей поверхностью раздела. Фаза может быть прерывной в случае ее получения измельчением (диспергированием) тел. Например совокупность кристаллов поваренной соли или капель ртути на поверхности. Система называется гомогенной (от лат. ген - род) или однородной, если содержит только одну фазу, и гетерогенной, если несколько фаз. Составными частями системы называют химически индивидуальные вещества, которые могут быть выделены из системы и существовать вне её самостоятельно. Независимыми компонентами называют составные части системы, наименьшее число которых достаточно для образования всех фаз данной системы. Число независимых компонентов равно числу составных частей системы минус число возможных равновесных реакций между этими составными частями. Например, смесь NH3, HC1 и NH4CI при низкой температуре будет трехкомпонентной системой. Если возникнет взаимодействие
NH3 + HC1 =NH4C1,
то система становится двухкомпонентной. Если в системе концентрации NH3 и HC1 будут связаны уравнением с(NH3) = с(НСl), то число компонентов будет равно единице. Состояние системы характеризуется совокупностью термодинамических параметров - давлением, температурой, объемом, концентрацией. Термодинамические параметры, которые можно менять без изменения числа и вида фаз называют степенями свободы или вариантностью системы. Если система не имеет ни одной степени свободы, то она называется инвариантной (нонвариантной, безвариантной), если одну степень свободы - моновариантной, если две – двух- или бивариантной и т.д. При рассмотрении фазового равновесия в гетерогенных системах ставится задача установить взаимосвязь между параметрами, характеризующими состояние изучаемой системы. Для анализа фазовых равновесий широко используется графическое отображение соотношений между параметрами состояния, называемое диаграммой состояния. Фазовые равновесия определяются правилом фаз Гиббса, являющимся основным законом фазового равновесия. В соответствии с ним для любых изолированных систем, находящихся в термодинамическом равновесии, число степеней свободы системы (С) равно числу ее компонентов (К) минус число фаз (Ф) плюс число независимых термодинамических параметров (N), способных оказывать влияние на равновесие системы:
C = K - Ф + N ,
Если на состояние равновесия системы влияют только давление и температура, то число степеней свободы C = K - Ф + 2. Если давление мало влияет на состояние равновесия, то C = K - Ф + 1. Как правило, влияние давления не учитывается в конденсированных системах или при р = const. В этом случае говорят об условной вариантности системы. Правило фаз позволяет предсказать, что в двухкомпонентной (К = 2) конденсированной (р = const) системе максимальное число равновесно-сосуществующих фаз равно трем, так как вариантность системы не может быть меньше нуля. Считая С = 0, по уравнению C = K - Ф + 1 получим Ф = 0 +2 + 1 = 3. Двухкомпонентные конденсированные системы (растворы, сплавы и др.) имеют большое практическое значение. В уравнениях состояния двухкомпонентных систем общее число переменных равно четырем: Т, р, с1, и с2. Это предполагает построение диаграмм состояния в четырехкоординатной системе измерений, что невозможно. В конденсированных системах давление можно не принимать во внимание, а из трех переменных Т, с1, и с2 две являются независимыми (Т, с1), а третью находят из соотношения с2 = 100 - с1, выражая концентрацию в массовых или молярных долях (%). Поэтому диаграммы состояния таких систем изображают на плоскости, откладывая по оси абсцисс температуру, а по оси ординат – концентрацию (%), отражающую химический состав системы. Изучение многокомпонентных гетерогенных систем проводят с помощью физико-химического анализа, который основан на установлении зависимости между физическими свойствами (тепловыми, электрическими, оптическими и др.) равновесной химической системы и ее химическим составом. На основании результатов изучения физических свойств равновесной системы строят диаграммы состояния в координатах «состав – свойство». По геометрическим особенностям диаграмм, совокупности линий на них, поверхностей и т.д. можно судить о характере взаимодействия компонентов, о наличии химических соединений, о числе, границах устойчивости, условиях существования различных фаз в системе. В основе исследования диаграмм состояния лежат принципы непрерывности и соответствия, сформулированные одним из создателей физико-химического анализа - академиком Н.С. Курнаковым. Принцип непрерывности устанавливает, что при непрерывном изменении параметров, определяющих состояние системы, свойства отдельных фаз её изменяются непрерывно. Свойства всей системы изменяются непрерывно до тех пор, пока не изменится число или характер её фаз. При появлении новых или исчезновении имевшихся фаз свойства системы в целом меняются скачком. Принцип соответствия гласит: каждой совокупности фаз, находящихся в равновесии в данной систем, отвечает на диаграмме определенный геометрический образ. Например, каждой твердой фазе на плоской диаграмме соответствует своя кривая температур начала кристаллизации (рис. 1). Физико-химический анализ особенно широко используют для изучения гетерогенных фазовых равновесий. Особенно велика его роль как теоретической основы производства специальных сталей, авиационных, полупроводниковых сплавов. Большое значение физико-химический анализ имеет для галургии, занимающейся исследованием равновесий в водно-солевых системах. Физико-химический анализ дает возможность, не прибегая к разделению системы на составные части, судить о свойствах системы, о наличии химических соединений и составе этих соединений. Физико-химический анализ имеет большое значение для контроля промышленных производственных процессов. Применение различных методов физико-химического анализа дает возможность проводить автоматический контроль процессов и автоматическое регулирование их. Одним из наиболее распространенных видов физико-химического анализа является термический, который представляет собой совокупность экспериментальных методов определения температуры, при которой в равновесной системе изменяется число фаз. Термический анализ основан на наблюдении кривых охлаждения. Кривые охлаждения – это графики зависимости изменения температуры от времени в данной системе. Если при охлаждении системы не происходит никаких фазовых превращений, то температура равномерно уменьшается. Если в системе происходит какое-либо превращение, сопровождающееся тепловым эффектом, то непрерывность хода кривой нарушается (рис. 1а).
Рис. 1. Кривые охлаждения (а) и диаграмма состояния системы с эвтектикой (б): L - расплав; L+A - расплав + первичные кристаллы A: L+B - расплав + первичные кристаллы В; A+E(A+B) - кристаллы А + твердая эвтектика; В+Е(А+В) - кристаллы В + твердая эвтектика: Е- эвтектика. На основании кривых охлаждения строят диаграмму состояния в координатах «температура - состав», по которой судят о наличии тех или других фаз, их числе, температуре кристаллизации смеси определенного состава и т.п. (см. рис. 1б). Для изучения равновесия между жидкой и твердой фазами системы применяют диаграммы состояния, называемые диаграммами плавкости. Они выражают зависимость температуры плавления смеси от ее состава. Диаграммы плавкости представляют собой совокупность линий, плоскостей и точек, отражающих химические процессы, происходящие в системе при изменении температуры или состава, отвечающих равновесию, таких как образование и распад химических соединений, появление и (или) исчезновение твердых или жидких растворов и т.п. На диаграмме линия температуры, выше которой компоненты системы находятся только в жидком состоянии, называется линией ликвидуса (от лат. liquor - жидкость), а линия ниже которой компоненты смеси находятся только в твердом состоянии – линией солидуса (от лат. solid - твердый). Точки на диаграмме состояния, отражающие равновесное состояние системы, при данных температуре и составе называют фигуративными. Исследование диаграмм плавкости проводят с помощью нод (или коннод), т. е. горизонтальных прямых, отвечающих постоянной температуре, соединяющих фигуративные точки двух находящихся в равновесии фаз. Особыми точками диаграмм плавкости являются точка эвтектики (т. Е) и точка перитектики (т. С). Обе точки отвечают состоянию двухкомпонетной системы, когда в равновесии одновременно находятся две твердые фазы и одна жидкая - их расплав. Однако процессы при охлаждении трехфазной системы существенно отличаются. В эвтектической точке одновременно выпадают две твердые фазы, а в перетектической одна выпадает, а другая растворяется, переставая существовать. Диаграммы плавкости можно разделить на четыре типа в зависимости от того, какая фаза выделяется из расплава: I тип - системы, компоненты которых А и В абсолютно растворимы друг в друге в жидком состоянии и абсолютно нерастворимы в твердом, называют неизоморфными (см. рис. 1б), т.к. при кристаллизации компоненты выделяются в виде смеси индивидуальных кристаллов А и В. Изоморфизм (от греч. изо - одинаковый и morphe – вид, форма) – это способность атомов, ионов или молекул сходных по строению замещать друг друга в кристаллических структурах. Неиоморфные диаграммы называют также диаграммами с эвтектикой (от греч. eutektik – хорошо плавящийся), т.к. эвтектическая смесь компонентов А и В плавится при наиболее низкой температуре по сравнению с чистыми компонентами А и В и их смесями.
кристаллизации которых из расплава выделяются твердые растворы с ограниченной областью взаимной растворимости (см. рис. 3 а-б), обозначаемые греческими прописными буквами α, β и т.д.
IV тип - системы, компоненты которых абсолютно растворимы друг в друге в жидком состоянии, а при кристаллизации которых из жидких расплавов выделяются химические соединения, плавящиеся конгруэнтно (без разложения) и инконгруентно (с разложением) (см. рис. 4 а-б).
Плавление называется конгруентным (от лат. congruentis - совпадающй), если состав жидкости совпадает с составом твердого химического соединения, из которого жидкость образовалась. При конгруетном плавлении компоненты смеси А и В образуют устойчивое соединение АmВn, не распадающееся при отвердевании расплава соответствующего состава. При инконгруентном плавлении соединение АmВn (АВ) является неустойчивым и распадается при отвердевании расплава. Это объясняется тем, что максимум, отвечающий температуре плавления инконгруентно плавящегося соединения (фигуративная т. F), не реализуется и попадает в область, находящуюся под линией ликвидуса одного из компонентов (в примере компонента В). Такой максимум называется скрытым. Поэтому химическое соединение является устойчивым только до температуры, отвечающей т.D. При более высокой температуре химическое соединение распадается на жидкий расплав L и кристаллы компонента В. Точка С называется переходной или перетектической. Химические соединения металлов называют интерметаллическими (межметаллическими) или интерметаллидами. Рассмотрим диаграмму состояния неизоморфной системы с простой эвтектикой (см. рис. 1б). Образующие систему два компонента А и В в жидком состоянии полностью растворимы друг в друге, а в твердом состоянии нерастворимы. Диаграмму состояния строят на основании кривых охлаждения (см. рис. 1а). Если чистое вещество А или В нагреть выше его температуры плавления (tA, tB), а затем охлаждать, то температура будет равномерно понижаться до момента образования твердой фазы. Кривые охлаждения чистых веществ будут иметь вид 1 и 6 на рис. 1а. Если смесь, состоящую из двух компонентов состава, отвечающего т. h, нагреть выше температуры плавления, то сначала будет происходить охлаждение однофазного жидкого расплава L. Число степеней свободы для расплава равно С = 2 -1 + 1 = 2, т.е. система двухвариантная. Это значит, что можно произвольно менять температуру и состав, сохраняя существование одной жидкой фазы. Наличие двух степеней свободы графически изображают плоскостью L, ограниченный снизу линией ликвидуса (аЕb) - (см. рис. 1б). По мере охлаждения при некоторой температуре расплав становится насыщенным относительно одного компонента А, который начинает кристаллизоваться. Выделяющаяся теплота кристаллизации замедляет скорость охлаждения и кривая (2, 3, 5, рис. 1а) в этом месте делает излом (точки g, k, r). Далее кривая идет не горизонтально, а постоянно понижаясь, так как состав жидкой фазы непрерывно изменяется. Таким образом, процесс кристаллизации вещества А из расплава отличается от процесса кристаллизации чистого вещества тем, что происходит при непрерывном изменении температуры и состава жидкой фазы (участок gE, kE, rЕ - рис, 1а). Число степеней свободы равно: C = 2 – 2 + 1 = 1, т.е. произвольно можно менять только один параметр - либо температуру, либо состав. Так как с момента образования твердой фазы система стала одновариантной, то между температурой и составом насыщенного раствора будет существовать связь, которая выражается графически кривой аЕb - рис. 1б. Это значит, что каждому составу соответствует определенная температура начала кристаллизации. Дальнейшее охлаждение приводит к тому, что раствор становится насыщенным относительно обоих веществ. При температуре tE оба компонента начинают кристаллизоваться одновременно. Состав жидкой фазы при этом не изменяется, кристаллизация идет при постоянной температуре. Кривая охлаждения дает горизонтальный участок. Длина горизонтального участка (ЕЕ - рис. 1а) пропорциональна количеству затвердевшего вещества. Число степеней свободы С = 2 – 3 + 1 = 0. Пока одновременно сосуществуют три фазы (две твердые и одна жидкая), система остается инвариантной. Графически это выражается на диаграмме состояния точкой Е, называемой эвтектической (см. рис. 1б). Отвердевание эвтектического расплава вызовет и изменение состава твердой фазы, так как она пополняется не только веществом А, но и веществом В. В момент исчезновения последней капли жидкости состав твердой фазы совпадает с составом исходного расплава (т.h смеси 3, рис.1б). После этого температура начнет снижаться, так как система с исчезновением жидкой фазы становится одновариантной. Для смеси 3 на рис. 1б показан процесс охлаждения: по линии ликвидуса (kЕ) указано изменение состава жидкой фазы, а по линии солидуса (tEC) - изменение состава твердой фазы. У смеси 4, точно отвечающей эвтектическому составу, при достижении температуры эвтектики будут выделяться сразу оба компонента при постоянной температуре tE (см. рис. 1а). Эвтектический состав имеет самую низкую температуру плавления (кристаллизации) по сравнению со смесями иных концентраций этой системы. Эвтектическая смесь кристаллизуется так же, как чистый компонент, хотя составные части эвтектики могут быть отделены друг от друга. Рассмотренная диаграмма позволяет решить вопрос, в каком состоянии находится система, образованная данной парой веществ, при различных температурах. Если нужно определить состав того или иного сплава (например, смесь 2 - рис. 1б), то, опуская перпендикуляр на ось состава, получим точку d, которая покажет, сколько в сплаве содержится компонента А (отрезок Bd) и компонента В (отрезок Ad), т.е.
где ω- массовые доли компонентов (ω(А) = 100 - ω(В)), %. Для определения соотношения масс твердой и жидкой фаз применяют правило рычага: массы сосуществующих фаз обратно пропорциональны отрезкам, на которые фигуративная точка системы делит прямую (ноду), соединяющую фигуративные точки фаз. Например, если состояние системы описывается фигуративной точкой n, то для определения состава и масс твердой и жидкой фаз проводят горизонтальную линию (ноду) через точку и до пересечения с границами области, в которой лежит эта точка. Перпендикуляр, опущенный из точки f, покажет состав кристаллической фазы (в данном случае кристаллы чистого вещества А), а перпендикуляр, опущенный на ось абсцисс из точки k, покажет состав жидкой фазы. Массы жидкой (L) и твердой фазы (А) определим по правилу рычага: массы равновесных фаз обратно пропорциональны длинам отрезков, на которые делит ноду фигуративная точка системы, т.е.
Жидкость состава точки К содержит компоненты А и В в следующем соотношении:
Таким образом, диаграмма состояния позволяет определить не только число фаз и их состав, но и массу каждой фазы.
Цель работы - освоение метода термического анализа, построение диаграммы плавкости бинарной неизоморфной системы.
Порядок выполнения работы 1. Регистрация кривых охлаждения образцов исследуемой смеси азобензол-нафталин с различной массовой долей компонентов проводится в следующем порядке: 1.1. Включить нагреватель водяной бани в сеть. 1.2. Поместить в неё комплект пробирок с исследуемыми смесями веществ и помещенными в них термопарами. Смеси состоят из нафталина и азобензола. Составы смесей и номера пробирок указаны в табл. 1.
Таблица 1
1.3. Построить диаграмму состояния в координатах «температура – состав». Точки температур окончания кристаллизации (Тк) соединить линией солидуса. 1.4. Определить состав эвтектической точки с помощью треугольника Таммана, построенного под диаграммой. Для этого проводят перпендикуляры из точек оси абсцисс, соответствующих исследуемым составам смесей, и откладывают на них длину горизонтальных отрезков кривых охлаждения при температуре кристаллизации эвтектики. Полученные точки соединяют прямыми, образующими треугольник. Вершина треугольника указывает состав эвтектики. Найденный по треугольнику Таммана состав эвтектики отметить на кривой солидуса. Провести через точки температур начала кристаллизации (Тн) плавные кривые ликвидуса, соединив их в точке состава эвтектики на кривой солидуса. 1.5. Включить самописец-потенциометр «КСП» в сеть. На передней панели потенциометра включить тумблер «Прибор». В процессе нагревания и расплавления веществ указатель температур на шкале прибора перемещается от комнатной температуры до 100°С. Регистрация температуры осуществляется при помощи термопар, подключенных к потенциометру марки «КСП». Это печатающий прибор, т.е. на диаграмме получается не линия, а точки с цифрой. Каждой точке с цифрой на диаграммной ленте соответствует температура смеси под тем же номером (см. табл. 1). 1.6. При температуре 70°С пробирки встряхнуть для равномерного расплавления смесей. При температуре 80°С включить тумблер «Диаграмма» на передней панели прибора. Перенести пробирку № 1 из водяной бани в воздушную рубашку (широкогорлая пробирка) для охлаждения. Последовательно с интервалом в 4 мин переносить из водяной бани остальные пробирки со смесями и помещать их в воздушные рубашки. 1.7. Водяную баню отключить от сети при температуре 90°С. 1.8. Запись кривых охлаждения прекратить после появления на диаграммной ленте для всех смесей второй вертикальной площадки, соответствующей температурной остановке кристаллизации эвтектики (~ 40°С). Выключить тумблер «Диаграмма», тумблер «Прибор». Оторвать диаграммную ленту с записью кривых охлаждения. 2. Построение диаграммы состояния по кривым охлаждения. Провести анализ всех кривых охлаждения, записанных на диаграммной ленте. Определить температуры начала Тн и окончания Тк кристаллизации каждой смеси; длительность температурной остановки l (в мм) для всех смесей при температуре кристаллизации эвтектики. Занести значения Тн, Тк, l в табл. 2. Таблица 2
Построить диаграмму состояния в координатах «температура – состав». Точки температур окончания кристаллизации (Тк) соединить линией солидуса. Определить состав эвтектической точки с помощью треугольника Таммана, построенного под диаграммой. Для этого проводят перпендикуляры из точек оси абсцисс, соответствующих исследуемым составам смесей, и откладывают на них длину горизонтальных отрезков кривых охлаждения при температуре кристаллизации эвтектики. Полученные точки соединяют прямыми, образующими треугольник. Вершина треугольника указывает состав эвтектики. Найденный по треугольнику Таммана состав эвтектики отметить на кривой солидуса. Провести через точки температур начала кристаллизации (Тн) плавные кривые ликвидуса, соединив их в точке состава эвтектики на кривой солидуса. 3. Расчет теплоты плавления компонентов. Если компоненты образуют между собой идеальный раствор (расплав), то зависимость растворимости твердого вещества в растворе (расплаве) от температуры выражают уравнением Шредера:
где N - молярная доля i-того компонента; ΔНПЛ - молярная теплота плавления i-того компонента, кДж/моль; Т - температура плавления i-того компонента, К. Интегральная форма уравнения Шредера для кривой ликвидуса вещества А:
Кривая ликвидуса компонента В опишется уравнением
где ΔН(А), ΔН(В) - молярные теплоты плавления чистых веществ А и В, кДж/моль; Т(А), Т(В) - температуры плавления чистых компонентов А и В, К; N(A), N(B) - молярные доли компонентов в расплаве, %; Т - температура плавления смеси, содержащей N расплавленного вещества, К. На основании диаграммы состояния и уравнений (1), (2), рассчитать теплоты плавления азобензола и нафталина. Рассчитать криоскопические константы заданного вещества (азобензола или нафталина) по формуле:
где К - криоскопическая константа; Т0 - температура кристаллизации чистого вещества, К; М - молярная масса вещества, г/моль; lПЛ = ΔΗпл/М - удельная теплота плавления, Дж/моль.
Контрольные вопросы 1. Важнейшие особенности физико-химического анализа как метода исследования многокомпонентных систем. 2. Сущность метода физико-химического анализа. 3. Основные принципы метода физико-химического анализа. 4. Каковы признаки и свойства гетерогенного фазового равновесия. 5. Сформулируйте правило фаз Гиббса и объясните, что понимают под терминами «фаза», «независимый компонент», «степень свободы». 6. Объясните принцип построения диаграммы состояния двухкомпонентной системы. 7. Разберите применение правила фаз Гиббса к процессу охлаждения системы азобензол - нафталин, используя диаграмму состояния. 8. Нарисуйте схематически диаграммы состояния для двухкомпонентных систем из: а) изоморфных и б) неизоморфных веществ (при р = const). Перечислите совокупности из одной, двух и трех сосуществующих фаз, в той и другой системах укажите поля фаз. 9. Как отражается на диаграмме состояния образование химического соединения? Нарисуйте диаграмму состояния с образованием химического соединения. 10. Определите вариантность системы, состоящей: а) из водного раствора хлоридов натрия и калия в присутствии кристаллов обеих солей и паров воды; б) из водного раствора, насыщенного хлоридом калия, в присутствии паров воды. 11. Чему равно максимальное число степеней свободы в одно-, двух-, трехкомпонентных системах при условии, что внешними факторами равновесия являются температура и давление?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Физическая химия:Учеб для.хим.спец.вузов/А.Г. Стромберг, Д.П. Семченко; под. ред. А.Г. Стромберга. - М.: Высш. шк., 2003. - 528 с. 2. Практикум по физической химии./ Под ред. В.В.Буданова, Н.К.Воробьёва. - М.:Химия, 2000. – 387 с. 3. Практические работы по физической химии. / Под ред. К.П. Мищенко, А.А. Равделя, А.М.Пономаревой.- СПб, изд-во «Профессия», 2002. – 384с. 4. Краткий справочник физико-химических величин /Под ред. А.А.Равделя, А.М.Пономаревой. - М.:Химия, 2002. - 327 с. 5. Киселева Е.В.,Каретников Г.С.,Кудряшов И.В. Сборник примеров и задач по физической химии.-М.:Высш.шк., 2001. – 389 с. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ К РАБОТЕ ПО ТЕРМИЧЕСКОМУ АНАЛИЗУ
Построить диаграмму фазового состояния двухкомпонентной системы А-В, зная температуру начала кристаллизации (Тн) системы (табл.3). Состав выражен в молярных процентах вещества В. 1. Обозначить на диаграмме точками: 1 - жидкий расплав, содержащий а мол. % вещества А при температуре T1 (табл. 4); 2 - расплав, содержащий а мол.% вещества А, находящийся в равновесии с кристаллами химического соединения; 3 - равновесие фаз одинакового состава; 4 -равновесие трех фаз. 2. Определить эмпирическую формулу химического соединения АmВn. 3. Начертить все типы кривых охлаждения, возможные для данной системы; указать на диаграмме, каким составам эти кривые соответствуют. Определить число степеней свободы системы в точках 1 - 4. 4. При какой температуре начнет отвердевать расплав, содержащий b мол. % вещества В (см. табл. 4)? При какой температуре он отвердеет полностью? Каков состав первых кристаллов? 5. Вычислить теплоту плавления ΔНi каждого компонента. 6. Какой компонент и в каком количестве (по массе) выкристаллизуется из системы, если 5 кг расплава, содержащего с мол. % вещества В, охладить до температуры Т2?
Таблица 3
Продолжение табл. 3
Окончание табл. 3
Таблица 4
Физико-химический анализ. Построение диаграммы плавкости двухкомпонентной системы
Составители: КОВРИГА Юрий Павлович СЛЕПУШКИН Вячеслав Васильевич СТИФАТОВ Борис Михайлович
Редактор В.Ф. Е л и с е е в а Технический редактор Г.Н. Ш а н ь к о в а
Подп.в печать 09.11.10 Формат 60х84 1/16. Бум.типор.№2 Усл.п.л. 1,16. Усл.кр.-отт. 1,16. Уч.-изд.л. 1,11 Тираж 50 экз.
Государственное образовательное учреждение высшего профессионального образования «Самарский государственный технический университет» 443100. г. Самара, ул. Молодогвардейская, 244. Главный корпус.
Отпечатано в типографии Самарского государственного технического университета 443100. г. Самара, ул. Молодогвардейская, 244. Корпус №8.
|
















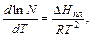
 (1)
(1) (2)
(2)