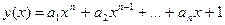ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Средства Matlab для проведения интерполяции

Для интерполирования функций в Matlab можно использовать операторы polyfit и polyval.

Оператор polyfit(x,у,n) находит массив коэффициентов а длиной (n+1) полинома степени n по массивам длиной m узлов х и значений функции в узлах у, m≥n+1. Этот полином аппроксимирует функцию у(х) по методу наименьших квадратов. Предполагается, что полином задается в виде

Если m=n+1, то программа возвращает коэффициенты интерполяционного полинома.

Оператор polyval(a,x) возвращает значение полинома в точке х, коэффициенты которого определены в векторе а.

Кроме это, существуют операторы позволяющие проводить интерполяцию одно- и многомерных данных.

interpft(y,n,dim)–аппроксимация периодической функции на основе быстрого преобразования Фурье (y – одномерный массив значений функции; n – число узлов в массиве значений):

spline(x,y,z) – интерполяция y=y(x) кубическим сплайном и вывод соответствующих значений в точках z. Для получения большей информации используется конструкция pp=spline(x,y):здесь командой v=ppval(pp,z) можно найти значения в точках z, a командой [xs,Coef,m,L]=unmkpp(pp) получить данные о векторе разбиений аргумента xs, коэффициентах Coef, m=length(xs), L=length(Coef)/m .

interp1(x,y,z),interp1(x,y,z,’method’)– одномерная табличная интерполяция (если y двумерный массив, интерполяция ведется по каждому столбцу; значения z должны входить в диапазон значений x). Можно указать метод интерполяции – кусочно-линейной (linear, по умолчанию), ступенчатой (nearest), кубической (cubic), кубическими сплайнами (spline). Функция interp1q(x,y,z)реализует быструю линейную интерполяцию на неравномерной сетке.

interp2(x1,x2,y,z1,z2),interp1(x1,x2,y,z1,z2,’method’)– двумерная табличная интерполяция y=y(x1,x2), аргументы должны меняться монотонно и заданы в формате функции meshgrid.

interp3(x1,x2,x3,y,z1,z2,z3),interp3(...,’method’)–трехмерная табличная интерполяция y=y(x1,x2,x3);

interpn(x1,x2,...,y,z1,z2,...),interp3(...,’method’)–многомерная табличная интерполяция y=y(x1,x2,...);

griddata(x1,x2,y,z1,z2),griddata(x1,x2,y,z1,z2,’method’)-двумерная табличная интерполяция на неравномерной сетке.

Для реализации программы полезными являются следующие операторы:

sum(x) и prod(x)– суммирование и произведение элементов вектора (для двумерного массива выполняется поиск сумм и произведений по столбцам).

diff(x),diff(x,n),diff(x,n,dim)– вычисление конечных разностей (первых, n-го порядка или по указанному измерению); если x – массив, берутся разности между столбцами:

Порядок выполнения работы

Написать соответствующие m-файлы сценарии и m-файлы функции для реализации следующих задач:

1. Провести интерполяцию функции Рунге на отрезке [-1,1] по формуле Лагранжа для n=11 при равномерном распределении узлов интерполяции.

2. Провести интерполяцию функции Рунге на отрезке [-1,1] по формуле Лагранжа для n=11 для чебышевских узлов.

3. Построить графики функции Рунге и ее интерполянт не менее чем в 100 узлах. Сравнить результаты.

4. Выбрать функцию согласно номера компьютера и провести ее интерполяцию по формуле Лагранжа при равномерном распределении узлов на заданном интервале для n=11 и n=6.

5. Провести интерполяцию по тем же узлам, используя стандартные функции Matlab.

6. Построить графики исходной функции и интерполянт не менее чем в 100 узлах. Сравнить результаты.

7. Вычислить и построить графики функций ошибок интерполяции.

Содержание отчета

1. Цель работы. Задание.

2. Описание метода решения, краткие сведения из теории (формулы, алгоритм и т.п.).

3. Программа (распечатка), ее описание.

4. Сравнение результатов расчета.

5. Краткие выводы по работе.