 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Лабораторная работа 7 Определение изменения энтропии в реальных системах.
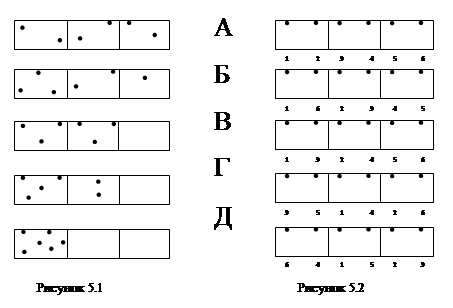
Основные понятия по теме Качественным отличием теплового движения молекул и атомов от других форм движения является его хаотичность и беспорядочность. Для характеристики теплового движения следует вывести количественную меру степени молекулярного беспорядка. Меру степени молекулярного беспорядка можно характеризовать термодинамической вероятностью, под которой понимают число микросостояний (микрораспределений), которыми может осуществляться рассматриваемое макро состояние (макро распределение). Термодинамическая вероятность отличается от математической вероятности, которая выражается дробным числом, не превышающим единицы. Термодинамическая вероятность выражается целым, и как известно, очень большим числом. Смысл термодинамической вероятности W поясним на следующем примере. Пусть имеется сосуд, разделенный мысленно на три отсека. В сосуде находится шесть частиц, например молекул, которые могут хаотически двигаться. И располагаясь тем или иным образом в отсеках сосуда, создавать определенные макрораспределения. Некоторые из возможных макрораспределений для указанного случая изображены на рисунке 5.1. Если частицы пронумеровать, то любое макрораспределение может быть реализовано рядом микрораспределений. На рис представлены некоторые возможные сочетания частиц (микрораспределения), дающие макрораспределение А. В теоретической физике доказано, что число микрораспределений, N частиц по n состояниям, например, N частиц в n отсеках, т.е. термодинамическая вероятность определяется формулой:
где N1- число частиц в первом состоянии (первом отсеке); N2 - число частиц во втором состоянии (втором отсеке)и т.д.
Вычислив термодинамические вероятности макросостояний А, Б, В, Г, Д (рисунок 5.1) соответственно, получим: WA = 90; WБ = 60; WB = 20; WГ= 15; WД =1. Как видно, наибольшая термодинамическая вероятность у равномерного распределения. Оно может осуществляться наибольшим числом способов (числом микрораспределений). Состояние, соответствующее равномерному распределению молекул по всему объему, реализуется огромным числом микрораспределений (при большом числе молекул) и является наиболее вероятным. Макроскопическое состояние газа с определенным средним значением параметров представляет собой непрерывную схему близких микроскопических состояний, отличающихся друг от друга распределением одних и тех же молекул в разных частях объема. Число этих непрерывно сменяющих друг друга микросостояний и характеризует степень беспорядочности макроскопического состояния всей системы. Это число есть термодинамическая вероятность W макросостояния. Однако, характеризовать степень хаотичности молекулярного движения с помощью W неудобно. Если система состоит из n независимых частей с соответствующими термодинамическими вероятностями W1 ,W2 , W3 , W4 ,…, Wn , то вероятность всей системы будет определяться произведением вероятностей Целесообразнее величину, характеризующую систему, представить не произведением, а суммой величин, характеризующих разные части системы. Больцман предложил в качестве величины, характеризующей меру беспорядочности теплового движения, взять не W , а величину, пропорциональную логарифму термодинамической вероятности Так как Величина S называется энтропией системы и зависит от значения макроскопических параметров ( V, P, T ), определяющих состояние системы. Следовательно, энтропия системы является однозначной функцией состояния системы. При расширении идеального газа в пустоту, средняя энергия молекул и их распределение по скоростям не меняется, а изменяется лишь распределение молекул в пространстве. При увеличении объема газа молекулы приобретают возможность попасть в области пространства, ранее не доступные. Благодаря этому, увеличивается число возможных микросостояний и степень беспорядочности увеличивается. Число таких возможных микросостояний для одной молекулы прямо пропорционально представленному объему V . Для идеального газа, содержащего N молекул в этом объеме
При расширении газа в пустоту и увеличении его объема от V1 до V2, энтропия газа возрастает на величину Направление течения процессов в природе устанавливает второй закон термодинамики. В формулировке Больцмана, выявляющей статический характер этого закона, он определяется так: все процессы в природе протекают в направлении, приводящем к увеличению вероятности состояния. Общее математическое выражение второго закона термодинамики дано Клаузисом
Впервые определение энтропии дано Клаузисом исходя из понятия приведенной теплоты. Физический смысл этой величины стал понятен после того, как Больцман связал ее с термодинамической вероятностью. При некоторой температуре внутренняя энергия тела известным образом распределяется между его молекулами и тело обладает определенной энтропией S. При сообщении телу некоторого количества теплоты DQ интенсивность и энергия теплового движения возрастает и становятся возможными новые микросостояния. Увеличение числа возможных микросостояний приводит к возрастанию энтропии тела на некоторую величину
Знак равенства соответствует обратимым, а неравенства - необратимым процессам. В изолированной (замкнутой) системе, состоящей из нескольких тел, при любом обратимом процессе энтропия системы остается неизменной. Представим, что процесс обмена теплотой между двумя телами обратимый, то есть температуры тел одинаковы. Изменение энтропии системы
Если температуры тел различны
Так как dS >0 , то энтропия системы при необратимом процессе в ней возрастает. Следовательно, процесс теплообмена протекает сам по себе в направлении, при котором степень беспорядка молекулярного движения возрастает, а следовательно, увеличивается энтропия и окончательное состояние оказывается более вероятным, чем начальное. Увеличение энтропии системы при теплообмене, указывает на то, что теплота самопроизвольно может передаваться от более нагретого тела, к менее нагретому. Используя понятие энтропии, второй закон термодинамики запишется
Знак равенства соответствует обратимым, а неравенства - необратимым процессам, происходящим в замкнутой системе. Отметим, что все реальные процессы, протекающие с конечной скоростью, являются необратимыми. Степень обратимости процессов в изолированной системе, можно определить, рассчитав изменение энтропии. В силу аддитивности энтропии, ее изменение для системы тел равно
где n - число тел системы. Изменение энтропии тела при переходе из состояния 1 в состояние 2
Для твердых и жидких тел можно считать
В качестве исследуемой системы выберем калориметр с водой и твердые тела, различной массы. Наличие внешнего стакана калориметра делают систему почти адиабатно - изолированной. Если в калориметр, содержащий определенное количество воды при заданной температуре Т0 , опустить тело с другой температурой Т1, происходит процесс теплообмена и установиться некоторая общая температура Т . Введем обозначение параметров, характеризующих тела системы. mT , cT , T1 - масса, удельная теплоемкость и начальная температура испытуемого тела; mK , cK , T0 - масса, удельная теплоемкость и начальная температура стакана калориметра; mM , cM , T0 - масса, удельная теплоемкость и начальная температура мешалки; mB , cB , T0 - масса, удельная теплоемкость и начальная температура воды калориметра. При выравнивании температуры произойдет изменение энтропии: тела стакана калориметра мешалки воды Изменение энтропии всей системы
Вопросы для самоконтроля 1 Физический смысл неравенства Клаузиуса. 2 Коэффициент полезного действия цикла Карно. 3 Физический смысл энтропии. 4 Вывод рабочей формулы для определения энтропии. Лабораторная работа 7 Определение изменения энтропии в реальных системах. Цель работы: определение изменения энтропии при нагревании различных тел. Материалы и оборудование: калориметр с мешалкой, нагреватель, набор тел, весы, набор гирь. Описание установки Установка рисунок 5.3 состоит из калориметра, включающего внешний стакан Д и внутренний стакан А , сосуда К с
Ход работы 1 Включить электроплитку Е, предварительно поставив на нее сосуд с водой К. 2 Определить массу испытуемого тела mT , массу мешалки mM и массу калориметрического стакана А. . 3 Поместить тело в стакан К нагревателя, а мешалку в калориметрический стакан. 4 Наполнить калориметрический стакан А на 2/3 водой, находящейся при комнатной температуре Т0. Определить массу воды mB. 5 Через 2-3 минуты после закипания воды в сосуде К, тело из него быстро перенести в калориметрический стакан А. Внешний стакан калориметра закрыть крышкой. 6 Наблюдая за изменением температуры в калориметре по микроамперметру или вольтметр - термометру, отметить показание n микроамперметра или температуру по вольтметр - термометру соответствующее равновесной температуре Т. Мешалку используют в конце процесса роста температуры, делая не более 3 - 5 перемешиваний. 7 По градуировочному графику отметить температуру Т. 8 Определить изменение энтропии системы в процессе теплообмена. 9 Аналогичные измерения проделать для двухдругих тел. При этом: количество воды в калориметрическом стакане А для всех тел брать одинаковым и с одинаковой температурой Т0 . 10 Построить график зависимости
|




 .
. , где k - постоянная Больцмана.
, где k - постоянная Больцмана. , то
, то  .
. и
и  .
. . Величина
. Величина  представляет собой количественную меру увеличения степени хаотичности теплового движения в данном процессе. Обратный процесс собирания молекул газа в одной половине представленного им объема самопроизвольно не осуществляется, так как он маловероятен. Если бы такой процесс имел место, то это означало бы , что степень беспорядка в газе и его энтропия могут самопроизвольно уменьшаться, и газ, находившийся в более вероятном состоянии самопроизвольно перешел бы в состояние, во много раз менее вероятное.
представляет собой количественную меру увеличения степени хаотичности теплового движения в данном процессе. Обратный процесс собирания молекул газа в одной половине представленного им объема самопроизвольно не осуществляется, так как он маловероятен. Если бы такой процесс имел место, то это означало бы , что степень беспорядка в газе и его энтропия могут самопроизвольно уменьшаться, и газ, находившийся в более вероятном состоянии самопроизвольно перешел бы в состояние, во много раз менее вероятное.

 , где
, где  ,
, 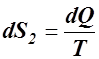 – изменение энтропии тел системы. Общее изменение dS энтропии всей замкнутой системы равно нулю.
– изменение энтропии тел системы. Общее изменение dS энтропии всей замкнутой системы равно нулю.
 (процесс теплообмена необратимый), то энтропия системы, состоящей из этих двух тел, изменяется на величину
(процесс теплообмена необратимый), то энтропия системы, состоящей из этих двух тел, изменяется на величину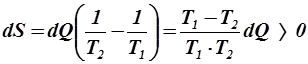

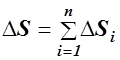
 - изменение энтропии одного тела, входящего в систему;
- изменение энтропии одного тела, входящего в систему;
 . Тогда,
. Тогда,  . Подставив
. Подставив  , получим
, получим





 электроплиткой и термопары В с микроамперметром. Исследуемое тело Б опускается в калориметрический стакан на нити, подвешенной на специальную планку.
электроплиткой и термопары В с микроамперметром. Исследуемое тело Б опускается в калориметрический стакан на нити, подвешенной на специальную планку. .
.