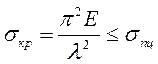ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Формулы Эйлера и Ясинского

Иркутский государственный университет путей сообщения

Лабораторная работа № 16

по дисциплине«Сопротивление материалов»

ОПЫТНОЕ ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ СИЛ

ПРИ ПРОДОЛЬНОМ ИЗГИБЕ

Кафедра ПМ

Лабораторная работа № 16

Опытное определение критических сил при продольном изгибе

Цель работы:исследование явления потери устойчивости сжатого стального стержня в упругой

стадии. Экспериментальное определение значений критических нагрузок сжатых

стержней при различных способах закрепления и сравнение их с теоретическими

значениями.

Общие положения

Сжатые стержни недостаточно проверять на прочность по известному условию:

где [σ] – допускаемое напряжение для материала стержня, P – сжимающая сила, F – площадь поперечного сечения.

В практической деятельности инженеры имеют дело с подвергающимися сжатию гибкими стержнями, тонкими сжатыми пластинами, тонкостенными конструкциями, выход из строя которых вызывается ен потерей несущей способности, а потерей устойчивости.

Под потерей устойчивости понимается потеря первоначальной формы равновесия.

В сопротивлении материалов рассматривается устойчивость элементов конструкций, работающих на сжатие.

Рассмотрим длинный тонкий стержень (рис. 1), нагруженный осевой сжимающей силой P.

P < P_кр P > P_кр

Рис. 1. Стержень, нагруженный осевой сжимающей силой P.

При малых значениях силы F стержень сжимается, оставаясь прямолинейным. Причем, если стержень отклонить от этого положения небольшой поперечной нагрузкой, то он изогнется, но при снятии ее стержень возвращается в прямолинейное состояние. Это значит, что при данной силе Pпрямолинейная форма равновесия стержня устойчива.

Если продолжить увеличивать сжимающую силу P, то при некотором ее значении прямолинейная форма равновесия становится неустойчивой и возникает новая форма равновесия стержня — криволинейная (рис. 1, б). Вследствие изгиба стержня в его сечениях появится изгибающий момент, который вызовет дополнительные напряжения, и стержень может внезапно разрушиться.

Искривление длинного стержня, сжимаемого продольной силой, называется продольным изгибом.

Наибольшее значение сжимающей силы, при котором прямолинейная форма равновесия стержня устойчива, называется критическим - P_кр.

При достижении критической нагрузки происходит резкое качественное изменение первоначальной формы равновесия, что ведет к выходу конструкции из строя. Поэтому критическая сила рассматривается как разрушающая нагрузка.

Формулы Эйлера и Ясинского

Задачу определения критической силы сжатого стержня впервые решил член Петербургской академии наук Л. Эйлер в 1744 г. Формула Эйлера имеет вид

(1)

где Е – модуль упругости материала стержня; J_min — наименьший момент инерции поперечного сечения стержня (поскольку искривление стержня при потере устойчивости происходит в плоскости наименьшей жесткости, т. е. поперечные сечения стержня поворачиваются вокруг оси, относительно которой момент инерции минимален, т.е. либо вокруг оси x, либо вокруг оси y);

(μ·l) – приведенная длина стержня, это произведение длины стержня l на коэффициент μ, зависящий от способов закрепления концов стержня.

Коэффициент μ называют коэффициентом приведения длины;его значение для наиболее часто встречающихся случаев закрепления концов стержня приведены на рис. 2:

а— оба конца стержня закреплены шарнирно и могут сближаться;

б— один конец жестко защемлен, другой свободен;

в— один конец закреплен шарнирно, второй имеет «поперечно-плавающую заделку»;

г — один конец жестко защемлен, второй имеет «поперечно-плавающую заделку»;

д— один конец заделан жестко, на другом шарнирно-подвижная опора;

е— оба конца жестко защемлены, но могут сближаться.

Из этих примеров видно, что коэффициент μпредставляет собой величину, обратную числу полуволн упругой линии стержня при потере устойчивости.

Рис. 2. Коэффициент μ для наиболее часто

встречающихся случаев закрепления концов стержня.

Нормальное напряжение в поперечном сечении сжатого стержня, соответствующее критическому значению сжимающей силы, также называется критическим.

Определим его исходя из формулы Эйлера:

(2)

Геометрическую характеристику сечения i_min, определяемую по формуле

, (3)

называют радиусом инерции сечения(относительно оси с J_min). Для прямоугольного сечения

С учетом (3) формула (2) примет вид:

(4)

Отношение приведенной длины стержня к минимальному радиусу инерции его поперечного сечения по предложению профессора Санкт-Петербургского института инженеров путей сообщения Ф.С. Ясинского (1856—1899) называют гибкостью стержняи обозначают буквой λ:

(5)

В этой безразмерной величине одновременно отражаются такие параметры: длина стержня, способ его закрепления и характеристика поперечного сечения.

Окончательно, подставив (5) в формулу (4), получим

(6)

При выводе формулы Эйлера предполагалось, что материал стержня упруг и следует закону Гука. Следовательно, формулу Эйлера можно применять только при напряжениях, меньших предела пропорциональности σ_пц, т. е. когда

Этим условием определяется предел применимости формулы Эйлера:

Величину, стоящую в правой части этого неравенства, называют предельной гибкостью:

ее значение зависит от физико-механических свойств материала стержня.

Для низкоуглеродистой стали Ст. 3, у которой σ_пц= 200 МПа, Е = 2·10⁵ МПа:

Аналогично можно вычислить значение предельной гибкости для других материалов: для чугуна λ_пред = 80, для сосны λ_пред = 110.

Таким образом, формула Эйлера применима для стержней, гибкость которых больше или равна предельной гибкости, т. е.

λ ≥ λ_пред

Понимать это надо так: если гибкость стержня больше предельной гибкости, то критическую силу надо определять по формуле Эйлера.

При λ < λ_пред формула Эйлера для стержней неприменима. В этих случаях, когда гибкость стержней меньше предельной, при расчетах пользуются эмпирической формулой Ясинского:

σ_кр = a – b·λ , (7)

где аи b— определяемые опытным путем коэффициенты, постоянные для данного материала; они имеют размерность напряжения.

При некотором значении гибкости λ_онапряжение σ_кр, вычисленное по формуле (7), становится равным предельному напряжению при сжатии, т. е. пределу текучести σ_т для пластичных материалов или пределу прочности при сжатии σ_вс – для хрупких материалов. Стержни малой гибкости (λ < λ_о)рассчитывают не на устойчивость, а на прочность при простом сжатии.

Таким образом, в зависимости от гибкости расчет сжатых стержней на устойчивость производится различно:

v у стержней большой гибкости (λ ≥ λ_пред) критические напряжения определяются по формуле Эйлера (6);

v у стержней средней гибкости (λ_о ≤ λ < λ_пред) критические напряжения определяются по формуле Ясинского (7);

v у стержней малой гибкости (λ < λ_о)расчет производится как при простом сжатии.

График зависимости σ_кр от λ для стержней из пластичного материала (низкоуглеродистой стали) показан на рис. 3.

Рис. 3. График зависимости σ_кр от λ для стержней из пластичного материала.

В табл. 1 приведены для некоторых материалов значения коэффициентов аи b,а также гибкостей λиλ_пред, в интервале между которыми для данного материала применима формула Ясинского.

Для стержней из чугунного литья (при λ < λ_пред ≈ 80) критические напряжения определяют по более сложной эмпирической зависимости:

где а= 776 МПа, b = 12 МПа, с = 0,053 МПа.

Таблица 1

Материал	а, Н/мм²	b, Н/мм²	λ_о	λ_пред
Сталь Ст. 2		0,70
Сталь Ст. 3		1,14
Сталь 20, Ст. 4		1,15
Сталь 45		1,67
Дюралюмин Д16Т		1,83
Сосна, ель	29,3	0,194	—