ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Гистограмма, полигон, кумулята и огива
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное Учреждение высшего профессионального образования «Юго-Западный государственный университет» (ЮЗГУ)
Кафедра финансов и кредита
Лабораторная работа №1 Методы группировки статистических данных
Выполнил студент 1 курса группы ЭБ-21 Гревцева Наталья
Проверил к.э.н., ст. преподаватель Обухова Анна Сергеевна Курск 2013 Выборочный метод. Статистическое распределение выборки При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом. При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность. Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, - генеральной совокупностью. Существуют различные способы формирования выборки (случайный, механический, типический, серийный (гнездовой)), но в математической статистике изучается собственно-случайная выборка с повторным отбором или бесповторным отбором. Собственно-случайная выборка формируется с помощью жеребьевки либо по таблице случайных чисел. Всем элементам генеральной совокупности присваиваются порядковые номера, затем производится выбор случайных номеров с помощью датчиков случайных чисел или из специальных таблиц, которые образуют порядковые номера для отбора. При повторном отборе единица наблюдения после извлечения из генеральной совокупности регистрируется и вновь возвращается в генеральную совокупность, откуда опять может быть извлечена случайным образом. При бесповоротном отборе элемент в выборку не возвращается. Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности n. Если объем генеральной совокупности велик, то разница между повторной или бесповторной выборками незначительна. Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна). Сущность выборочного метода заключается в том, что выводы, сделанные на основе изучения части совокупности (случайной выборки), распространяются на всю генеральную совокупность. Математическая статистика занимается обоснованием такого приема, применяя теорию вероятностей. Вариационный ряд Элементами выборки { Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если выборка соответствует дискретной случайной величине, то вариационный ряд представляет собой таблицу, которая ставит в соответствие каждому значению Например, на основе наблюдения за ростом растения получены n=50 значений числа почек на единицу длины ветки (пример 3.1, табл.3.2). Понятно, что здесь мы имеем пример дискретной случайной величины, так как число почек может быть только целым. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала (a,b), то строим интервальный вариационный ряд с помощью группировки вариант. Существуют различные способы группировки вариант, среди которых является метод равных интервалов. Рассмотрим алгоритм группировки методом равных интервалов. 1. Сначала определяют число интервалов m. Для этого обычно применяют формулу Стреджесса: m = 1 + 3,22 × lg n. (3.1) Число m округляют до целого значения. Приведем еще несколько формул расчета числа интервалов: m = m = 1,72 m = В программе Excel есть процедура «Гистограмма», которая умеет строить вариационный ряд и вычисляет число интервалов по формуле (3.1с). Пример применения процедуры «Гистограмма» приведен ниже. В табл. 3.1 вычислены рекомендуемые формулами (3.1), (3.1а), (3.1b) и (3.1с) числа интервалов. Значения приведены с округлением до целого. Таблица 3.1
2. Далее вычисляют границы интервалов. Приведём два способа определения границ. В первом способе длину интервала вычисляют по формуле. h= xmin=min {xi}, xmax={xi}, (3.2a) и определяют границы интервалов по формулам: x0=xmin –h/2, x1=x0+h, …., xm=xm-1+h (3.3a) При таком выборе хmin попадает в середину первого интервала, а xmax – в середину последнего, и число интервалов m. Во втором способе длина интервала и границы вычисляются по формулам: h= x0=xmin , x1=x0+h, …., xm=xm-1+h. (3.3б) При этом хmin относится к первому, а xmax – к последнему интервалам. h= 3. После определения границ интервалов вычисляют для каждого j-того интервала Xср.j и частоту nj т.е. число таких элементов xi выборки, которые удовлетворяют условиям
Вычисляют также для каждого интервала относительную частоту (частость): wj = nj/n , (3.6) накопленные частоты и накопленные относительные частоты (накопленные частости): njнакопл= Вариационный ряд записывают в виде таблицы (табл.3.2)
Приведем два способа определения границ. В первом способе длину интервала определяют по формуле. h= определяют границы интервалов по формулам: x0=7-10/2=2, x1=x0+h, …, xm=xm-1+h. (3.3a) При таком выборе xmin попадет в середину первого интервала, а xmax - в середину последнего, и число интервалов равно m. Во втором способе длина интервала и границы вычисляются по формулам: h= x0 = xmin , x1 = x0+h, …, xm = xm-1 + h. (3.3б) При этом хmin относят к первому, а хmax - к последнему интервалам
Таблица 3.2
Замечание. Вариационный ряд можно задать двумя столбцами: интервалами (или их серединами) и частотами. Остальные столбцы легко вычисляются. При повторном отборе единица наблюде6ния после извлечения из генеральной совокупности регистрируется и вновь возвращается генеральная совокупность, откуда опять может быть извлечена случайным образом. При бесповторном отборе элемент в выборку не возвращается. Число единиц (Элементов) статистической совокупности называется ее объемом. Объем генеральн6ой совокупности обозначается N, а объем выборочной совокупности n. Если объем генеральной совокупности велик, то разница между повторным или бесповторными выборками незначительна. Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна). Сущность выборочного метода заключается в том, что выводы, сделанные на основе изучения части совокупности (случайной выборки), распространяется на всю генеральную совокупность. Математическая статистика занимается обоснованием такого приема, применяя теорию вероятности.
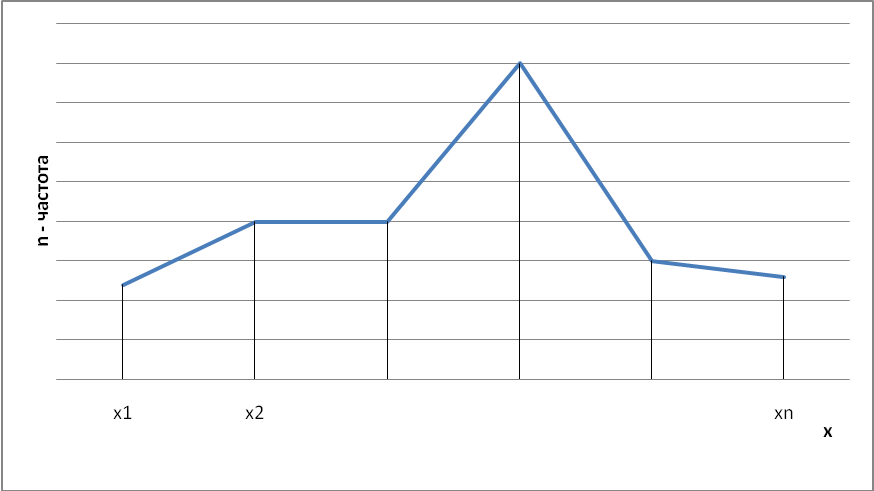
Гистограмма, полигон, кумулята и огива Для графического изображения вариационного ряда используются гистограмма, полигонов, кумулята и огива. Для дискретного вариационного ряда полигон частот представляет собой многоугольник (рис. 3.1), ограниченный осью ОХ и ломанной, соединяющей точки (
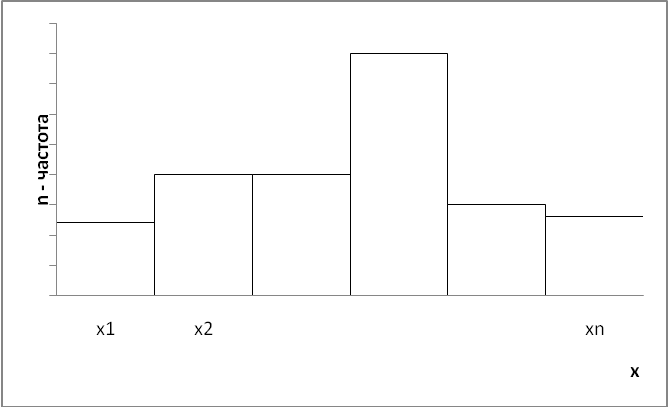
Рис. 3.1 Для интервального вариационного ряда с равными интервалами гистограмма частот состоит из прямоугольников, ширина которых равна длине интервала, а высота пропорциональна частоте (рис. 3.2). Для интервального ряда с неравными интервалами ширина прямоугольника равна длине соответствующего интервала, а высота пропорциональна плотности частоты, равной отношению частоты к длине интервала. В общем случае гистограмма состоит из прямоугольников, ширина каждого из которых равна длине соответствующего интервала, а площадь прямоугольников пропорциональна частоте или относительной частоте. При этом сумма площадей всех прямоугольников равна сумме частот или единице. Обычно гистограмму состоят по относительным частотам, так чтобы сумма площадей прямоугольников была равна единице. Тогда ломаная, соединяющая середины верхних сторон прямоугольников (полигон), является аналогом графика плотности вероятностей распределения. При больших объемах выборки полигон относительных частот приближенно отображает график функции плотности вероятностей генерального распределения.
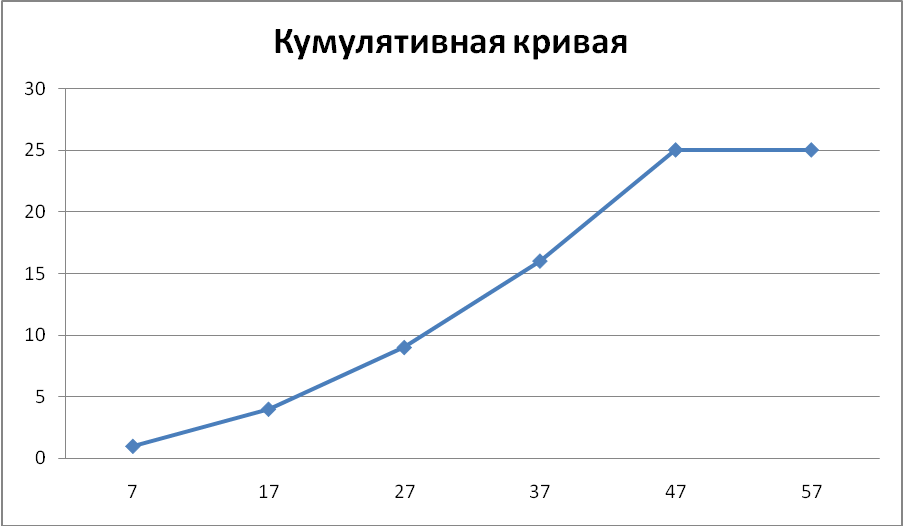
Рис. 3.2 Полигон накопленных частот строится так же, как и полигон частот, при этом вместо частот используются накопленные частоты. Для непрерывного признака на оси абсцисс откладываются значения середин интервалов, а на оси ординат – накопленные частоты или накопленные частости. Полученные точки соединяют гладкой кривой, которая называется кумулятивной кривой (или кумулятой). Кумулята, построенная по накопленным частотам, при больших объемах выборки является приближением к графику функции распределения вероятностей генеральной совокупности. Огива в англоязычной литературе определяется как сглаженный график накопленных частот, т.е. это кумулята. В российских учебниках по статистике огива определяется по-разному. В одном случае огива — это ломаная, соединяющая точки, полученные при откладывании значений вариант на оси ординат, а накопленные частот — на оси абсцисс (Шмойлова Р. А., Минашкин В. Г., Садовникова Н. А., Шувалова Е. Б. Теория статистики: учебник,М.: Финансы и статистика, 2006). В другом случае огива строится так же, как и кумулята, только вместо накопленных частот используются частоты, подсчитанные с условием «больше чем» (Теория статистики: учебник / под ред.: «проф. Г. Л. Громыко. — М.: ИНФРА-М, 2000). Таблица 3.2
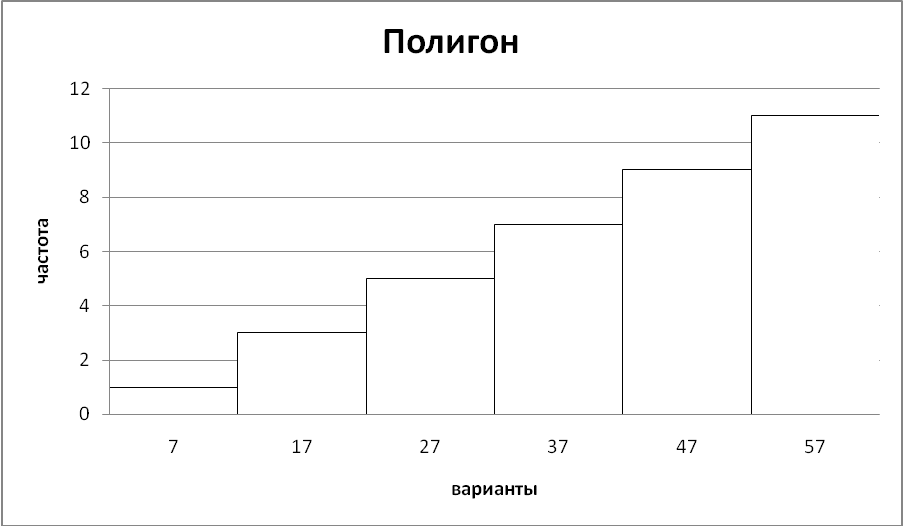
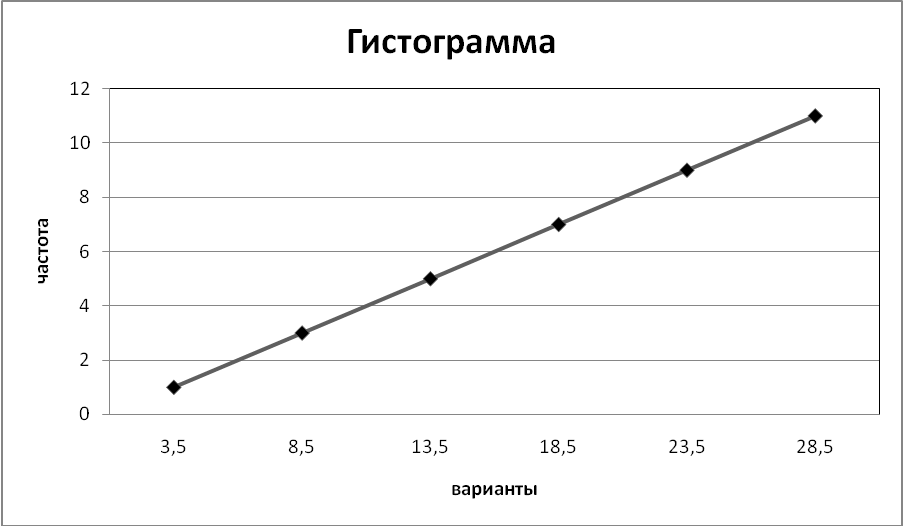
Введем в программе Excel исходные данные из таблицы 3.2 и построим полигон (рис.3.3) и гистограмму (рис. 3.4).
Рис. 3.3
Рис. 3.4 Построим кумулятивную кривую. Введем варианты и накопленные частоты в Exel, выделим диапАзон A1:B2, выберем тип диаграммы «Точечная диаграмма со значениями, соединенными сглаживающими линиями». После преобразований получим диаграмму, изображенную на рис. 3.5.
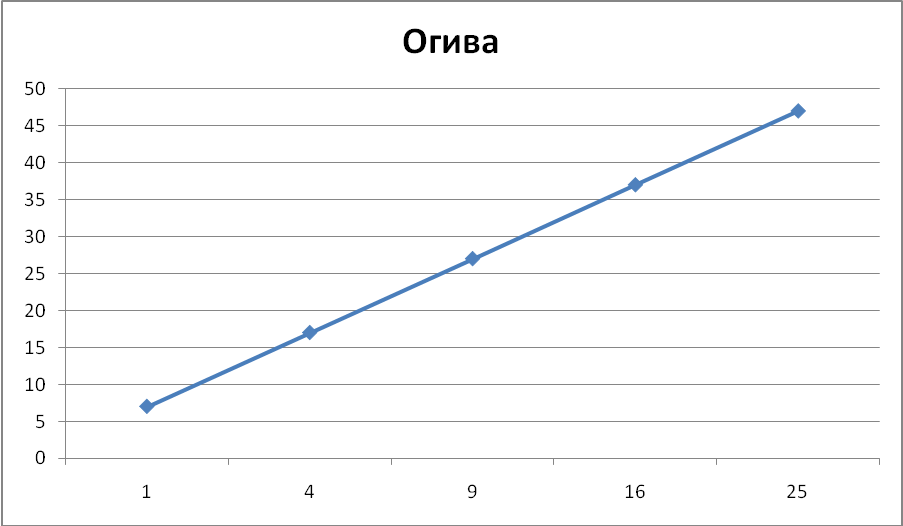
Рис. 3.5 Если мы просто поменяем местами столбцы A1 :A6 и B1: B6, то диаграмма преобразуется в огиву. После замены заголовка и форматирования осей получим диаграмму на рис. 3.6. Эта кривая соответствует определению огивы из первого из указанных выше учебников.
Рис. 3.6 В одном случае огива – это ломаная, соединяющая точки, полученные при откладывании значений вариант на оси ординат, а накопленных частот – на оси абсцисс (Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник. – М.: Финансы и статистика, 2006). В другом случае огива строится так же, как и кумулята, только вместо накопленных частот используются частоты, подсчитанные с условием «больше чем» (Теория статистики: учебник / под ред. проф. Г.Л. Громыко. – М.: ИНФРА-М,2000).
|



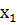 ,
, 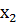 …,
…, 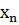 } являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (a,b). Другими словами, выборка может быть частью генеральной совокупности, которая соответствует дискретной или непрерывной случайной величине.
} являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (a,b). Другими словами, выборка может быть частью генеральной совокупности, которая соответствует дискретной или непрерывной случайной величине.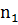 . Такой ряд носит название дискретный вариационный ряд.
. Такой ряд носит название дискретный вариационный ряд.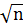 - 0,013n , (3.1a)
- 0,013n , (3.1a)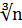 (3.1b)
(3.1b)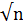 + 1. (3.1c)
+ 1. (3.1c)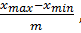
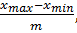 (3.2б)
(3.2б)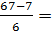 10
10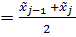 (3.4)
(3.4) j-1 < xi ≤
j-1 < xi ≤  j . (3.5)
j . (3.5)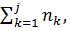 wjнакопл=
wjнакопл= 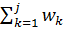 =
= 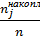 , j= 1,…,m. (3.7)
, j= 1,…,m. (3.7)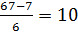 , xmin= min{xi}, xmax{xi}, (3.2a)
, xmin= min{xi}, xmax{xi}, (3.2a)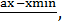 (3.3а)
(3.3а)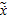 j-1,
j-1, 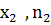 ),…,(
),…,( 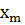 ,
, 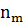 ), (
), ( 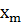 ,0)
,0)