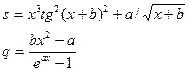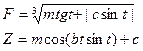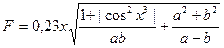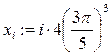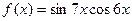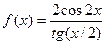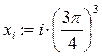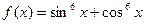ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Простейшие математические вычисления 12
Задача 1. Найти ребро куба, равновеликого шару, площадь поверхности которого равна площади боковой поверхности прямого кругового конуса, у которого высота вдвое меньше, чем длина образующей. Объем этого конуса равен 1. Анализ. Основные геометрические формулы, используемые при расчете. Объем конуса - Площадь боковой поверхности конуса - Соотношение в конусе между радиусом основания, высотой и длиной образующей - Площадь поверхности шара - Объем шара - Выполнение. 1.Запустите программу MathCad через Главное меню (Пуск \Программы\MathSoft Apps\MathCad) или с рабочего стола щелкнув по ярлыку Mathcad 2001 Professional. 2. Откройте панель инструментов с помощью команды Вид \ Панели инструментов \ Математика (View\Toolbars\Arithmetic) или Arithmetic (Математика) щелчком на кнопке Arithmetic Toolbar (Панель инструментов \ Математика) на панели инструментов Math (Математика). На рабочем поле появится панель инструментов Math.
На ней, щелкнув на кнопке Calculator (Калькулятор) - 3. Для удобства расчета будем обозначать каждую из вычисляемых величин отдельной переменной. Объем конуса обозначим как V и присвоим ему значение 1. Оператор присваивания вводится символом « : = » щелчком по значку на панели Calculator (Калькулятор) или кнопкой Assign Value (Присвоить значение) на панели инструментов Arithmetic (Арифметика). Итак, надо ввести V:=1. В документе появится полноценный оператор присваивания: V: =l. 4. Путем несложных преобразований получим, что радиус основания конуса можно вычислить по формуле Вводить эту формулу следует слева направо. Порядок ввода этой формулы следующий: - с начала введите r : = ; - затем введите знак корня произвольной степени, находящийся на панели инструментов Calculator (Калькулятор) или комбинацией клавиш CTRL+V. Щелкните на черном квадратике, стоящем на месте показателя степени и введите цифру 3. - щелкните на квадратике, замещающем подкоренное выражение, нажмите клавиши [V][*]. - введите знак квадратного корня: кнопка Квадратный корень на панели инструментов Calculator (Калькулятор) или клавиша[\] и цифру 3. - прежде чем вводить знаменатель, дважды нажмите клавишу ПРОБЕЛ. Обратите внимание на синий уголок, который указывает на текущее выражение. Предполагается, что знак операции связывает выбранное выражение со следующим. В данном случае это безразлично, но в целом этот прием позволяет вводить сложные формулы, избегая ручного ввода дополнительных скобок, нажмите клавишу [/]. - чтобы ввести число 5. Введите формулы для вычисления длины образующей и площади боковой поверхности конуса:
Указание знака умножения между переменными обязательно, так как иначе MathCad сочтет, что указана одна переменная с именем из нескольких букв. 6. Для вычисления радиуса шара R введите формулу 7. Для вычисления объема шара введите формулу 8. Заключительная формула а = 0.7102. 9. Вернитесь к самому первому выражению и отредактируйте его. Вместо значения 1 присвойте переменной значение 8. Сразу же перейдите к последней введенной формуле и обратите внимание, что результат расчета сразу же стал отражать новые начальные данные.
2. Вычисление дискретной функции с дискретным аргументом. Задача 2. Построить таблицу значений функции 1. Определим диапазон значений дискретного аргумента. Для этого введите выражение i:=0..25. При вводе диапазона щелкните по кнопке 2. Зададим изменение аргумента х на заданном интервале [0, 4p2]. Введите следующую формулу:
Для введения индекса аргумента используйте кнопку «Нижний индекс» на панели «Арифметика» или клавишу на клавиатуре «[». 3. Ниже введенной формулы введите 4. Вычислим функцию. Для этого наберите формулу:
5. Ниже этой формулы наберите f(x,i) и введите знак « = ». Появится таблица значений функции (Рис. 1).
Рисунок 1 - Таблицы значений дискретного аргумента и функции Задания Задание 1.Вычислить значения функции при заданных значениях её переменных.
Задание 2. Вычислить дискретную функцию с дискретным аргументом и представить в виде таблиц.
Содержание отчета и его форма 1. Форма отчета – письменная с электронным приложением. 2. Отчет выполняется в тонкой тетради. 3. Отчет, должен содержать: - тему; - цель лабораторной работы; - краткий отчет выполнение лабораторной работы в тетради. - выводы. 4. Электронное приложение должно содержать протокол выполнения задний лабораторной работы. (три экземпляра сохраняемые в трех разных местах) Пример оформления письменного отчета Лабораторная работа № Тема (название) Цель. См. выше Цель работы Краткий конспект алгоритма выполнения лабораторной работы Выводы. Отметка о защите работы
Контрольные вопросы и защита работы Контрольные вопросы: 1. Опишите интерфейс MathCad. 2. Как записываются формулы в MathCad. 3. Опишите, как вычисляются функции с дискретным аргументом.
Защита лабораторной работы включает: - Выполнение работы на компьютере, - ответы на контрольные вопросы, - предоставление отчета.
12 |



 .
. .
.
 .
. . Объем куба – V= a3.
. Объем куба – V= a3.
 , появляется панель управления Arithmetic (Арифметика) или Calculator (Калькулятор)
, появляется панель управления Arithmetic (Арифметика) или Calculator (Калькулятор) .
. , можно воспользоваться комбинацией клавиш CTRL+SHIFT+P или на панели инструментов Math (Математика) щелкните по кнопке
, можно воспользоваться комбинацией клавиш CTRL+SHIFT+P или на панели инструментов Math (Математика) щелкните по кнопке  , появится еще одна панель Greek (Греческий алфавит),на ней щелкните по кнопке
, появится еще одна панель Greek (Греческий алфавит),на ней щелкните по кнопке  ;
;  .
. .
. . Использовать переменную V во второй раз не следует, так как теперь мы определяем совершенно другой объем.
. Использовать переменную V во второй раз не следует, так как теперь мы определяем совершенно другой объем. позволит получить окончательный результат. После этого снова наберите имя переменной а и нажмите клавишу « = »или щелкните на кнопке Evaluate Expression (Вычислить выражение) на панели инструментов Arithmetic (Счет). После формулы появится знак равенства и вычисленный результат.
позволит получить окончательный результат. После этого снова наберите имя переменной а и нажмите клавишу « = »или щелкните на кнопке Evaluate Expression (Вычислить выражение) на панели инструментов Arithmetic (Счет). После формулы появится знак равенства и вычисленный результат. на отрезке [0, 4p2].
на отрезке [0, 4p2]. на панели инструментов. На панели Matrix (Матрицы)щелкните по«m…n».
на панели инструментов. На панели Matrix (Матрицы)щелкните по«m…n». .
. и введите знак « = ». Появится таблица значений дискретного аргумента (Рис. 1).
и введите знак « = ». Появится таблица значений дискретного аргумента (Рис. 1). .
.
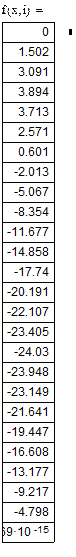



 g = x (sin x3+cos2y)
g = x (sin x3+cos2y)