 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Синтез АСР температуры в методической печи
Цель работы –выполнить расчет и исследование АСР температуры в методической печи с учетом требований к качеству функционирования системы.
Выбрать простейший регулятор, обеспечивающий поддержание заданных параметров переходного процесса, и определить его настройки для стабилизации температуры в сварочной зоне методической нагревательной печи, имеющей запаздывание tоб, постоянную времени Тоб, коэффициент передачи koб и максимальное возмущающее воздействие xвх. Технологические требования: допустимая статическая ошибка не должна превышать Dxстдоп;максимальноединамическое отклонение - x1доп; допустимое время регулирования - tрдоп в соответствии с заданным типовым законом (табл. 1). Проверку соответствия качества системы заданным требованиям выполнить на ПЭВМ с использованием прикладного пакета моделирования. Табл. 1.
Краткие сведения из теории Автоматический регулятор - это комплекс устройств, подключаемых к объекту регулирования и обеспечивающих автоматическое поддержание заданных значений его регулируемых величин или автоматическое изменение их по определенному закону. Определяющим условием при выборе регулятора и расчета его настроек является качество регулирования, определяющее точность поддержания технологического режима и ее экономическую эффективность. При этом под выбором регулятора понимают выбор закона регулирования. Закон регулирования - это математическая зависимость между входной и выходной величинами регулятора. Наиболее широкое распространение получили регуляторы непрерывного действия, использующие линейные законы регулирования
где x вых.р - выходная величина регулятора; xвх.р - его входная величина; C1, C2, C3 - коэффициенты пропорциональности, называемые параметрами настройки регулятора; t - время. Сумма трех составляющих образует ПИД-закон регулирования. При отсутствии отдельных составляющих будут образовываться П-, И-, ПИ-, ПД-законы регулирования. В соответствии с реализуемыми законами регулирования регуляторы непрерывного действия делятся на различные типы. 1. Пропорциональные регуляторы, у которых выходная величина xвых.р связана с входной величиной xвх.рсоотношением xвых.р = kрxвх.р, где kр - коэффициент передачи регулятора. Передаточная функция П-регулятора имеет вид Wп(p) = kр. 2. Интегральные регуляторы, у которых изменение выходной величины пропорционально интегралу изменения входной
где kр1 - коэффициент передачи И-регулятора, характеризующий скорость исполнительного механизма при отклонении входной величины. Передаточная функция И-регулятора Wи(p) = kр1/p. 3. Пропорционально-интегральные регуляторы, у которых изменение выходной величины пропорционально как изменению входной величины, так и интегралу ее изменения
где Tи - время изодрома. Передаточная функция такого ПИ-регулятора
4. Пропорционально-дифференциальные регуляторы, которые оказывают суммарное воздействие на регулирующий орган, пропорциональное как отклонению регулируемой величины, так и скорости ее отклонения
где Tп - время предварения. Передаточная функция регулятора имеет вид Wпд(p)=kр(1+Tпp). 5. Пропорционально-интегрально-дифференциальные регуляторы, у которых изменение выходной величины пропорционально отклонению регулируемой величины, интегралу этого изменения и скорости изменения этой величины
Передаточная функция ПИД-регулятора
В соответствии с законами регулирования настройками этих регуляторов являются: для П-регулятора - коэффициент передачи kp, % хода регулирующего органа/единица измерения регулируемой величины; для И-регулятора - коэффициент передачи kр1, % хода регулирующего органа/с×единица измерения регулируемой величины; для ПИ-регулятора - коэффициент передачи kp, % хода регулирующего органа/единица измерения регулируемой величины; время изодрома Tи, с; для ПИД-регулятора - коэффициент передачи kp; время изодрома Tи, с; время предварения Tп, с. Настройки непрерывных регуляторов П-, И-, ПИ-, и ПИД-действия позволяют получить любой из трех типовых оптимальных процессов регулирования: апериодический процесс с минимальным временем регулирования, с 20%-ным перерегулированием или процесс с минимальной квадратичной площадью отклонения с min òx2dt.
Рис. 1. Типовые переходные процессы регулирования
Апериодический процесс (граничный) с минимальным временем регулирования, кроме минимальной величины общего времени регулирования tр, характеризуется отсутствием перерегулирования и минимальным регулирующим воздействием. Применяют тогда, когда требуется минимальное время регулирования, перерегулирование не допускается, а динамическое отклонение x1 может быть сравнительно большим (рис. 1, а). Процесс с 20%-ным перерегулированием и минимальным временем первого полупериода колебаний рекомендуется применять в тех случаях, когда допускают определенную величину перерегулирования, но предъявляют более жесткие, чем в предыдущем случае, требования к величине максимального динамического отклонения регулируемой величины (рис. 1, б). Процесс с min òx2dt - процесс с минимальной квадратичной площадью отклонения характеризуется наибольшим перерегулированием (40 - 45%) и временем регулирования, а также наибольшим регулирующим воздействием, но и наименьшей величиной динамического отклонения (рис. 1, в). Регулятор выбирается по известным характеристикам объекта регулирования и возмущения и при заданных требованиях, предъявляемых к качеству переходных процессов. Сначала следует выбрать тип регулятора, затем закон регулирования и соответствующие параметры его настроек. С приемлемой для практических целей точностью большинство объектов регулирования в черной металлургии можно аппроксимировать статическим объектом с запаздыванием:
или астатическим объектом с запаздыванием
Исходные данные для выбора регулятора: 1. Статические и динамические параметры объекта регулирования, определяемые по кривой разгона: чистое запаздывание tоб; постоянная времени Тоб; их отношение tоб/Тоб; коэффициент передачи koб. 2. Максимально возможные значения возмущений по нагрузке xвх, % хода регулирующего органа, - пиковых, скачкообразных длительных и непрерывных монотонных (при непрерывных возмущениях должна быть известна также максимальная скорость возмущения х'вх, %/с). 3. Требуемые показатели качества регулирования объекта. При установке регулятора непрерывного действия должны обеспечиваться: максимальное динамическое отклонение x1доп (единицах измерения регулируемой величины); допустимое или желаемое перерегулирование x2доп/x1доп, %; допустимое остаточное отклонение (статическая ошибка) Dxстдоп(единицах измерения регулируемой величины); предельно допустимое время регулирования tрдоп, с.
При инженерных методах выбора и расчета регуляторов закон регулирования и значение настроек регулятора могут быть определены по следующей методике: 1. Определить тип регулятора по величине отношения tоб/Tоб.
2. Рассчитать величину допустимого динамического коэффициента регулирования
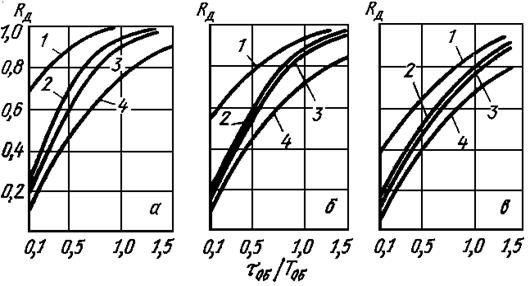
3. По графикам Rд(tоб/Tоб), приведенным на рис. 2 для заданного типового оптимального процесса регулирования, выбрать простейший регулятор (закон регулирования), обеспечивающий при заданном значении tоб/Tоб значение динамического коэффициента регулирования Rд £ Rддоп.
Рис. 2. Динамические коэффициенты регулирования на статических объектах при процессах: а - апериодическом; б - с 20%‑ным перерегулированием; в - с min òx2dt; 1 - И-регулятор; 2 - П-регулятор; 3 - ПИ-регулятор; 4 - ПИД-регулятор
4. По графикам, приведенным на рис. 3 для статических ОР, проверить, обеспечит ли выбранный регулятор допустимое время регулирования tр.
Рис. 3. Время регулирования на статических объектах: а - апериодический процесс; б - процесс с 20%-ным перерегулированием; в - процесс с min òx2dt; 1 - 4 - соответственно И-, П-, ПИ, ПИД-регуляторы
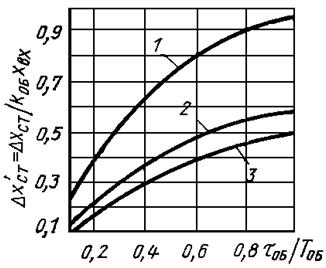
5. Для П-регулятора, необходимо по рис. 4 найти величину статической ошибки, и если она больше допустимой, то вместо П-регулятора нужно установить более сложный регулятор.
6. Для выбранного регулятора подсчитать значения настроек по формулам, приведенным в табл. 2.
Рис. 4. Остаточное отклонение на статических объектах: 1 - апериодический процесс; 2 - процесс с 20%-ным перерегулированием; 3 - процесс с min òx2dt
Табл. 2.
Порядок работы 1) Краткое описание объекта регулирования, составление функциональной схемы АСР. 2) Выбор типа регулятора и расчет его параметров, исходя из требований к АСР. 3) Составление структурной схемы АСР с выбранным регулятором и заданной моделью ОР. 4) Анализ устойчивости и определение по ЛЧХ запасов устойчивости по модулю и фазе. 5) Определение степени устойчивости и колебательности по корням характеристического уравнения, оценка времени регулирования. 6) Определение вынужденной ошибки при произвольном задающем воздействии. 7) Анализ качества АСР (прямые оценки) путем моделирования на ПЭВМ; 8) Коррекция параметров регулятора с использованием известных инструментариев пакета Matlab. 9) Анализ качества АСР со скорректированными параметрами регулятора и выбор наилучшего варианта. 10) Оценка степени устойчивости и колебательности после коррекции параметров регулятора. 11) Оценка запасов устойчивости и качества конечного варианта АСР.
Литература
1. Попов Е.П. Теория линейных систем автоматического регулирования и управления. - М.: Наука. 1989. 2. Теория автоматического управления. Учеб. для вузов. Часть 1/ Под редакц. А.А.Воронова. - М.: Высшая школа, 1986. 3. Глинков Г.М., Климовицкий М.Д. Теоретические основы автоматического управления металлургическими процессами. - М.: Металлургия, 1985. 4. Технические средства автоматики / Кишнев В.В., Иванов В.А., Тохтобаев Г.М., Афанасьев А.А. - М.: Металлургия,1981. 5. Попович Н.Г., Ковальчук А.В., Красовский. Автоматизация производственных процессов и установок. - Киев: Вища школа, 1986. 6. Стрыгин В.В. Автоматика и вычислительная техника. - М.: Высшая школа, 1977. 7. Автоматическое управление металлургическими процессами: Учебник для вузов./ Беленький А.М., Бердышев В.Ф., Блинов О.М., Каганов В.Ю. - М.: Металлургия, 1989. 8. Шевакин Ю.Ф., Рытиков А.М., Касатин Н.И. Технологические измерения и приборы в прокатном производстве. - М.: Металлургия, 1973. 9. АСУ ТП современных балочных прокатных станов / Под редакц. Б.Б.Тимофеева и В.И.Попельнуха. - М.: Металлургия, 1984. 10. Выдрин В.Н., Федосиенко А.С. Автоматизация прокатного производства. - М.: Металлургия, 1984. 11. Котов К.И., Шершевер М.А. Автоматическое регулирование и регуляторы. Учебник для техникумов. - М.: Металлургия, 1987.
|



 ,
, ,
,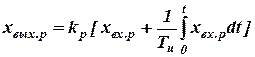 ,
, .
. ,
,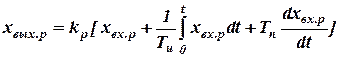 .
.


 .
.

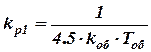 ;
; ;
; ;
; ;
; ;
; ;
; ; Ти = 0.6Тоб;
; Ти = 0.6Тоб; ; Ти = Тоб;
; Ти = Тоб; ; Ти=2.4tоб; Тп=0.4tоб.
; Ти=2.4tоб; Тп=0.4tоб. ; Ти=2.0tоб; Тп=0.4tоб.
; Ти=2.0tоб; Тп=0.4tоб. ; Ти=1.3tоб; Тп=0.5tоб.
; Ти=1.3tоб; Тп=0.5tоб.