 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ НАГРУЗКИ ЗВЕЗДОЙ
ОПД.Ф.09 ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
Методические указания к выполнению лабораторных работ по дисциплине
Часть 1. Электротехника
Специальность 280402 Природоохранное обустройство территорий Уфа 2011 УДК 378.147.88:621.3.024 ББК 74 58:31.21 М 54
Рекомендовано к изданию методической комиссией факультета землеустройства и лесного хозяйства (протокол № __ от ______2011 г.)
Составители: ст. преподаватель Толмачева Л.Р., ст. преподаватель Филиппова О.Г.
Рецензент: заведующий кафедрой электрических машин и электрооборудования д.т.н., профессор Аипов Р.С.
Ответственный за выпуск: заведующий кафедрой автоматики и электротехники к.т.н., доцент Галимарданов И.И. ОГЛАВЛЕНИЕ
Лабораторная работа № 1
Исследование электрической цепи переменного тока при последовательном соединении катушки индуктивности и конденсатора. Исследование резонанса напряжений Цель работы Исследовать электрическую цепь с последовательно соединенными активным сопротивлением, конденсатором и катушкой с регулируемой индуктивностью. Выяснить условия возникновения резонанса напряжений.
Теоретические сведения В неразветвленной электрической цепи (рисунок 1.1) при прохождении гармонического тока i = Im sinωt на зажимах создается гармоническое напряжение, равное алгебраической сумме мгновенных значений напряжений на отдельных элементах (второй закон Кирхгофа): u = uR + uL + uC . (1.1)
Рисунок 1.1 Неразветвленная электрическая цепь
На рисунке 1.2,а показаны кривые тока и напряжения, при этом напряжение на активном сопротивлении (uR) совпадает по фазе с током, на индуктивном элементе напряжение (uL) опережает ток на угол π/2, а на емкостном элементе напряжение (uC) отстает от тока на угол π/2.
Рисунок 1.2 Напряжение на активном, индуктивном, емкостном сопротивлении при гармоническом токе: а) кривые напряжений; б) векторная диаграмма
Построение векторной диаграммы (рисунок 1.2, б) осуществляется с учетом известных фазовых соотношений. Вектор напряжения на резисторе совпадает по фазе с вектором тока, на конденсаторе он отстает от вектора тока на 90°, а на катушке опережает вектор тока на 90°. Сумма этих векторов напряжений на элементах цепи, даст вектор напряжения источника. Из векторной диаграммы определяем напряжение на зажимах всей цепи: U = где UR = IR – активная составляющая напряжения, UL = IXL – индуктивная составляющая напряжения, UС = IXС – емкостная составляющая напряжения.
Полное сопротивление цепи найдем из закона Ома, либо из треугольника сопротивлений (рисунок 1.3): z = z = где Х = XL - XС – реактивная составляющая сопротивления; XL = ω L – индуктивная составляющая реактивного сопротивления; XС = ω = 2πf – угловая частота (f = 50 Гц).
Рисунок 1.3 Треугольник сопротивлений
Сдвиг фаз определяется из треугольника напряжений или сопротивлений: φ = arctg В зависимости от знака величины (ХL – XC) сдвиг фаз может быть либо положительным (φ > 0 – индуктивный характер цепи), либо отрицательным (φ < 0 – емкостный характер цепи), но всегда φ ≤ ±π/2. В неразветвленной электрической цепи при последовательном соединении катушки индуктивности и конденсатора может возникнуть резонансное явление – резонанс напряжений, при котором ток в цепи и напряжение на входе совпадают по фазе. Название “резонанс напряжений” отражает равенство действующих значений напряжений на катушке индуктивности и конденсаторе. При резонансе напряжений сопротивления реактивного участка равны между собой: ХL = XC. (1.6) Таким образом, при резонансе напряжений Х = ХL – XC = 0, следовательно, полное сопротивление цепи минимальное и равно активному z = R.
Экспериментальная часть
На рисунке 1.4 приведена электрическая схема опыта. Буквенно-цифровые обозначения элементов и приборов, используемых в схеме: ЛАТР – лабораторный автотрансформатор; РА1 – амперметр; РV1 – вольтметр, регистрирующий величину входного напряжения, регулируемого автотрансформатором; РV2 и РV3 – вольтметры, измеряющие напряжения на индуктивном и емкостном элементах; L1 – катушка индуктивности с выдвижным сердечником; С1 – батарея конденсаторов; Д – датчик тока.
Рисунок 1.4 Схема неразветвленной электрической цепи
Порядок проведения работы 1.4.1 Ознакомиться с оборудованием и приборами лабораторной установки и записать их паспортные данные в таблицу 1.1.
Таблица 1.1 Данные приборов и оборудования
В установке использован осциллограф для визуального наблюдения за опережением или отставанием напряжения от тока по фазе на угол jв зависимости от соотношения между напряжениями UL и UC. Для одновременного наблюдения на экране осциллографа двух процессов в нем имеется электронный коммутатор. Клеммы коммутатора расположены с левой стороны осциллографа («Вход 1», «Вход 2»). Ручками «Усиление 1» и «Усиление 2» устанавливают требуемую величину амплитуд исследуемых сигналов. Смещение осциллограмм по вертикали относительно друг друга осуществляют ручкой «Смещение». 1.4.2 Собрать электрическую схему установки (рисунок 2.4), уяснить назначение отдельных ее элементов и дать проверить ее преподавателю. 1.4.3 Перед подачей напряжения к установке рукоятку ползунка Т1 устанавливают на «0». На экране осциллографа будут две горизонтальные линии, которые совмещают в одну, пользуясь ручкой «Смещение». С помощью ЛАТРа устанавливают напряжение 30 или 60 В (по указанию преподавателя). Величину этого напряжения сохранять неизменной. 1.4.4 Изменяя индуктивное сопротивление цепи, при различных значениях
Таблица 1.2 Параметры электрической цепи при различных видах нагрузки
1.4.5 По результатам измерений построить векторные диаграммы в масштабе для трех различных режимов исследуемой цепи ХL > XC ; ХL = XC ; ХL < XC. 1.4.6 Проанализировать результаты эксперимента и сделать выводы о влиянии реактивного сопротивления на сдвиг фаз. 1.4.7 При анализе векторных диаграмм уясняют, какие параметры относительно друг друга сдвинуты по фазе, что вызывает этот сдвиг, какой вид нагрузки преобладает, что определяет величину тока и напряжения на отдельных участках цепи. Выводы записать в отчет.
1.5 Контрольные вопросы
1.5.1 Изобразите треугольники напряжений, сопротивлений и мощностей для цепи с активно-емкостной нагрузкой. Чем они отличаются от треугольников для активно-индуктивной нагрузки? 1.5.2 Что называют резонансом напряжений, и каким образом он достигается? 1.5.3 Какую величину имеет коэффициент мощности и угол j при резонансе напряжений? 1.5.4 Каким образом можно определить в эксперименте состояние резонанса напряжений (по показаниям приборов)? 1.5.5 Может ли представлять опасность режим резонанса напряжений? 1.5.6 Где может применяться резонанс напряжений в технике?
Лабораторная работа № 2
ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ НАГРУЗКИ ЗВЕЗДОЙ
Цель работы Исследование трехфазной цепи, соединенной звездой при симметричной и несимметричной нагрузке. Вычисление соотношений между номинальными линейными и фазными напряжениями и токами, выяснение роли нейтрального провода. Теоретические сведения
При соединении обмоток фаз звездой, их концы объединены в один общий узел, который называется нейтралью, а начала обмоток соединяются с источником тока проводами, которые называются линейными. В трехфазной системе напряжение между линейными проводами называется линейным (UAВ, UBС, UCА, Uл), а напряжение между началом и концом одной обмотки называется фазным (UA, UB, UC, Uф) (рисунок 2.1).
Рисунок 2.1 Схема соединения обмоток фаз приемника звездой
Ток, идущий по линейному проводу называется линейным, а ток, идущий непосредственно через потребитель, называется фазным. При соединении нагрузки звездой линейный и фазный токи одинаковы: Iф = Iл (2.1) Приемник с одинаковым сопротивлением всех трех фаз называется симметричным (ZA = ZB = ZC), при этом токи всех фаз одинаковы, и одинаковы сдвиги фаз относительно соответствующих напряжений, ток в нейтральном проводе равен нулю. У симметричной трехфазной системы фазные напряжения равны UA = UB = UC = Uф и образуют симметричную систему векторов (рисунок 2.2).
Рисунок 2.2 Векторная диаграмма напряжений и токов при соединении нагрузки звездой
Из диаграммы следует, что линейные векторы напряжения равны между собой и сдвинуты относительно друг друга на 120°. Uл = 2 Uфcos30° =
Экспериментальная часть
На рисунке 2.2 приведена электрическая схема опыта. Буквенно-цифровые обозначения элементов и приборов, используемых в схеме: РА1-РА3 – амперметры для измерения линейных (фазных) токов; РА4 – амперметр нейтрального провода; РV1- РV3 – вольтметр для измерения линейных и фазных напряжений; UAB, UBС, UСА – линейные напряжения; Q – автомат трехфазной сети.
Рисунок 2.3 Электрическая схема трехфазной нагрузки, включенной по схеме «звезда с нейтральным проводом»
Порядок проведения работы
2.4.1 Ознакомиться с оборудованием и приборами лабораторной установки и записать их паспортные данные в таблицу 2.1.
Таблица 2.1 Данные приборов и оборудования
2.4.2 Собрать электрическую схему установки и уяснить назначение отдельных ее элементов. В качестве нагрузки фаз приемника используется ламповый реостат (активная нагрузка). 2.4.3 После проверки схемы преподавателем, исследовать режимы. 2.4.3.1 Симметричная нагрузка без нейтрального провода. Симметричную нагрузку осуществляют включением одинакового количества ламп одной мощности в каждой фазе. 2.4.3.2 Симметричная нагрузка с нейтральным проводом. 2.4.3.3 Несимметричная нагрузка с нейтральным проводом. Несимметричную нагрузку создают путем изменения сопротивления в фазах, при этом в нейтральном проводе появится ток IN. 2.4.3.4 Несимметричная нагрузка без нейтрального провода. 2.4.3.5 Восстановив симметрию, выполняют обрыв линейного провода без нейтрального провода, отсоединяя один из линейных проводов, при выключенной схеме установки. 2.4.3.6 Обрыв линейного провода с нейтральным проводом. 2.4.3.7 Короткое замыкание фазы. Режим короткого замыкания в фазе выполняют при отключенном нулевом проводе, предварительно установив симметричную нагрузку и выключив схему установки, при этом накоротко замыкают проводником клеммы батареи ламп. 2.4.4 Результаты измерений занести в таблицу 2.2. 2.4.5 Построить векторные диаграммы напряжений в масштабе для каждого режима без нейтрального провода. 2.4.6 Для всех режимов вычислить мощность фаз и полную мощность нагрузки. Р = РА + РВ + РС (2.3) Рф = Uф Iф cosj (2.4) 2.4.7 Установить влияние нейтрального провода на работу системы; по полученным результатам измерений проверить справедливость соотношений между линейными и фазными величинами и сделать выводы.
2.5 Контрольные вопросы 2.5.1 Что называется соединением звездой и каковы его особенности? 2.5.2 Каковы соотношения между фазными и линейными величинами токов и напряжений при симметричной нагрузке? 2.5.3 В каком случае отсутствует ток в нулевом проводе и почему? 2.5.4 Почему на нулевой провод не ставят предохранитель? 2.5.5 Какие потребители в хозяйстве, как правило, имеют симметричную и несимметричную нагрузку? 2.5.6 Какую роль выполняет нулевой провод при несимметричной нагрузке?
Лабораторная работа № 3 |





 , (1.2)
, (1.2) ; (1.3)
; (1.3) , (1.4)
, (1.4) – емкостная составляющая реактивного сопротивления;
– емкостная составляющая реактивного сопротивления;
 = arctg
= arctg  . (1.5)
. (1.5)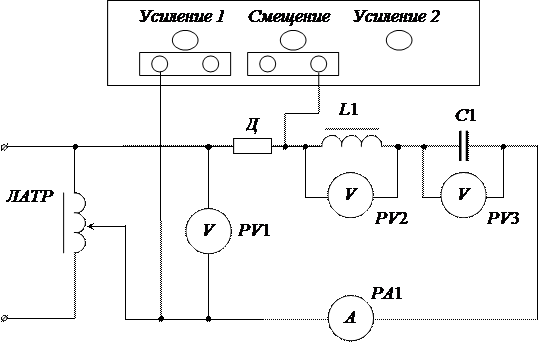
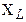 снять показания приборов, в том числе для резонанса напряжений при UL = UC . В лабораторной работе индуктивное сопротивление ХL изменяют перемещением сердечника в катушке, причем по мере выдвижения сердечника индуктивное сопротивление катушки уменьшается. Результаты измерений записать в таблицу 1.2.
снять показания приборов, в том числе для резонанса напряжений при UL = UC . В лабораторной работе индуктивное сопротивление ХL изменяют перемещением сердечника в катушке, причем по мере выдвижения сердечника индуктивное сопротивление катушки уменьшается. Результаты измерений записать в таблицу 1.2.
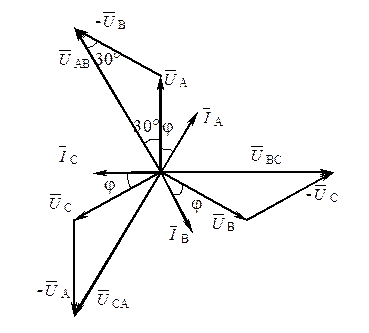
 - вектор, начинающийся в точке В и заканчивающийся в точке А, т.е первая буква индекса обозначает точку конца вектора, вторая – начало. Из диаграммы следует, что между действующими значениями линейных и фазных напряжений справедливо соотношение
- вектор, начинающийся в точке В и заканчивающийся в точке А, т.е первая буква индекса обозначает точку конца вектора, вторая – начало. Из диаграммы следует, что между действующими значениями линейных и фазных напряжений справедливо соотношение Uф . (2.2)
Uф . (2.2)