 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Закономерности свечения дискретных центров
Лабораторная работа № 7.6
Затухание люминесценции
(учебно-методическое пособие к лабораторному практикуму)
Составил проф. Михайленко В.И Утверждено на заседании кафедры протокол №4 от 16 января 2003 г.
Одесса-2003
Теоретическая часть
Общая характеристика люминесценции
Кроме термодинамически равновесного теплового излучения, существуют также неравновесные излучения, одним из видов которого является люминесценция. По определению С.И.Вавилова ЛЮМИНЕСЦЕНЦИЕЙ НАЗЫВАЕТСЯ ИЗБЫТОЧНОЕ НАД ТЕПЛОВЫМ ИЗЛУЧЕНИЕ, ЕСЛИ ЕГО ДЛИТЕЛЬНОСТЬ ПРЕВЫШАЕТ 10-10 с. Это определение позволяет отличить люминесценцию, спектр которой, как правило, расположен в видимом диапазоне, от равновесного теплового излучения, которое при комнатной температуре в видимой части спектра практически отсутствует. В отличие от отражённого света, который исчезает практически мгновенно после перекрытия падающего луча, люминесценция характеризуется определенной «инерционностью», т.е. после прекращения подвода энергии от внешнего источника люминесценция продолжается от 10-10 с до нескольких секунд и более. По механизму возбуждения люминесценции различают следующие её виды. 1. Фотолюминесценция - возбуждение молекул вещества ультрафиолетовым (или видимым) излучением. 2. Корпускулярная люминесценция - возбуждение молекул ударами микрочастиц (чаще всего электронов). 3. Хемилюминесценция - возникновение свечения в ходе химических реакций, в которых энергия химических процессов превращается непосредственно в световую. Чрезвычайно интересный вид хеми-люминесценции - биолюминесценция - свечение живых объектов (бактерий, светлячков, рыб и др.). 4. Электролюминесценция - свечение, возникающее при помещении некоторых полупроводников в электрическое поле, под действием которого электроны переходят на более высокие энергетические уровни с последующими переходами на более низкие уровни энергии, сопровождающиеся испусканием световых квантов. Этот вид люминесценции широко используется для отображения информации (дисплеи, цифровые табло и др.). В зависимости от механизма «высвечивания» аккумулированной энергии различают два типа люминесценции: · свечение дискретных центров, · рекомбинационное свечение. Свечение дискретных центров характерно для изолированных молекул (газы, разбавленные жидкие и твёрдые растворы), Этот тип люминесценции характерен тем, что все процессы, начиная от акта поглощения фотона и заканчивая излучением фотона люминесценции, происходят в одном и том же центре (атоме, молекуле). При рекомбинационном свечении поглощение фотона возбуждающего света приводит к отрыву электрона от атома (внутренний фотоэффект). Далее этот электрон некоторое время перемещается внутри кристалла и затем рекомбинирует с каким-либо ионом, излучая избыток энергии в виде фотона люминесценции.
Закономерности свечения дискретных центров
Рассмотрим основные законы свечения дискретных центров на примере люминесценции изолированных сложных молекул. Энергия молекулы в этом случае состоит из энергии электронов Wэл и энергии колебаний атомов Wкол, имеющих дискретный ряд значений. При этом Wкол <<Wэл и колебательные уровни расположены более тесно по сравнению с электронными, Типичная схема энергетических уровней молекулы показана на рис. 1.
Пусть на молекулу, находящуюся в основном электронном состоянии Исходя из закона сохранения энергии, получим:
Это состояние молекулы является неравновесным и поэтому малоустойчивым. В связи с этим возбуждённая молекула быстро (за время ~10-12 с) отдаёт избыток своей энергии окружающей среде и переходит на уровень
Из формул (1) и (2) следует
Как видно из формулы (3), частота света люминесценции меньше, чем частота возбуждающего света vл< vв. Этот результат был эмпирически установлен ещё в 1852 г. Дж. Стоксом и носит название правила Стокса. Дальнейшие исследования показали, что возможны (хотя и маловероятны) случаи, когда молекула исходно находится на возбуждённом колебательном уровне Такая люминесценция называется антистоксовой, но так как такие переходы маловероятны, то интенсивность антистоксовой люминесценции крайне мала. Более общим по сравнению с правилом Стокса, является закон Стокса-Ломмеля: Спектр люминесценции всегда сдвинут в область меньших частот по сравнению со спектром поглощения (рис.2).
На рис.2 n0 – наименьшая частота фотона, способного перевести молекулу в возбуждённое электронное состояние, т.е. вызвать переход
При v< v0 энергии фотона недостаточно для перевода молекулы в возбужденное электронное состояние (однако такой переход возможен, если молекула добавит к hn0 часть колебательной энергии). Важнейшими характеристиками люминесценции являются квантовый hк и энергетический hээ выход люминесценции. Квантовый выход люминесценции равен отношению числа фотонов люминесценции Nл к числу возбуждающих фотонов Nв:
Энергетический выход люминесценции равен отношению энергии люминесценции Wл к энергии возбуждающего света Wв:
Первый закон Вавилова: Квантовый выход люминесценции остаётся постоянным при частотах возбуждающего света n>n0 , а приn <n0 с уменьшением частоты быстро падает до нуля (рис. 3). Второй закон Вавилова: Энергетический выход люминесценции при v< v0 возрастает по мере увеличения частоты, а при частотах >v0 уменьшается до нуля (рис.4).
Поскольку
Затухание люминесценции
1.3.1.Затухание люминесценции дискретных центров
Интенсивность люминесценции после прекращения возбуждения постепенно убывает (затухает). Пусть в некоторый момент времени t число возбуждённых молекул вещества равнялось N . Убыль числа возбуждённых молекул -dN за интервал времени dt пропорционален N и dt, т.е.
где a - постоянная затухания. Очевидно, Интегрируя (8), получим:
откуда
Так как интенсивность люминесценции пропорциональна скорости уменьшения числа возбуждённых молекул
где I0- интенсивность люминесценции в момент времени t=0. Из (10) видно, что люминесценция дискретных центров затухает по экспоненциальному закону. Обычно для характеристики скорости затухания люминесценции наряду с постоянной a используют понятие среднего времени жизни молекулы в возбуждённом электронном состоянии t, которое численно равно времени, в течение которого число возбуждённых молекул уменьшается в е раз. Из (9) следует:
1.3.2. Затухание рекомбинационного свечения В рекомбинационном свечении убыль числа свободных электронов вызвана их рекомбинацией с ионами кристаллической решетки. Убыль числа свободных электронов -dN пропорциональна их числу Nэ, числу ионов решётки Nu и промежутку времени dt :
В простейшем случае, когда
Интегрируя выражение (13), получим:
и окончательно:
Интенсивность люминесценции пропорциональна
Для люминофора, используемого в данной лабораторной работе, уже при малых временах затухания (t<0.1 с) начинает выполняться неравенство
Закон затухания (16) выведен в предположении, что Nэ = Nu. В более общем случае, когда число свободных электронов не равно числу ионов
где I0 - интенсивность люминесценции в момент времени t=1 , а коэффициент затухания g лежит в пределах
Экспериментальная часть
Целью настоящей работы является определение закона затухания люминесценции для данного вещества и соответствующего типа люминесценции. Схема установки показана на рис.5.
Исследуемое вещество (люминофор) помещают в положение 1. В течение заданного времени его облучают светом лампы S , а затем помещают в положение 2 так, чтобы свет люминесценции попадал на фотоэлемент ФЭ, фототок которого регистрируется гальванометром Г. Между перемещениями люминофора из положения 1 в положение 2 его, согласно заданию, выдерживают в промежуточном положении определённое время (t=l,2,...c). Отсчёт по гальванометру в положении 2 берут в тот момент, когда его стрелка (световой луч) максимально отклоняется от нулевого положения. Далее, вследствие высвечивания люминофора интенсивность люминесценции падает, и стрелка гальванометра возвращается к нулю. После окончания высвечивания люминофора проводится следующий опыт (с другим временем выдержки в промежуточном состоянии). Результаты измерений заносят в таблицу.
3. Вывод расчётной формулы 3.1. В том случае, если в исследуемом образце происходит свечение дискретных центров, то затухание люминесценции описывается формулой (10). Прологарифмировав это выражение, получим:
Обозначив
т.е. в этом случае зависимость lnI от t будет линейной (рис.6-б). В других же координатах (например, lnI от lnt эта зависимость будет нелинейной (рис.6-в)
3.2. Для рекомбинационного свечения закон затухания имеет вид (17). Логарифмируя это выражение, получим:
Обозначив
т.е. в данном случае зависимость lnI от lnt будет линейной (рис. 76).
|



 Рис.1
Рис.1 -энергия i-го колебательного уровня молекулы, находящейся в n-ом электронном состоянии (n= 1,2).
-энергия i-го колебательного уровня молекулы, находящейся в n-ом электронном состоянии (n= 1,2). и наинизшем колебательном состоянии
и наинизшем колебательном состоянии  падает фотон возбуждающего света hvв. Молекула поглощает этот фотон и переходит на некоторый колебательный уровень
падает фотон возбуждающего света hvв. Молекула поглощает этот фотон и переходит на некоторый колебательный уровень  возбуждённого электронного состояния (переход 1, рис.1).
возбуждённого электронного состояния (переход 1, рис.1).
 (переход 2, рис.1). Далее молекула перейдёт на один из колебательных уровней
(переход 2, рис.1). Далее молекула перейдёт на один из колебательных уровней  основного электронного состояния
основного электронного состояния  иизлучит фотон люминесценции hvл (переход 3, рис.1). Для перехода 3 из закона сохранения энергии следует:
иизлучит фотон люминесценции hvл (переход 3, рис.1). Для перехода 3 из закона сохранения энергии следует:

 основного электронного состояния
основного электронного состояния  идалее, поглотив фотон, возвращается на наинизший колебательный уровень
идалее, поглотив фотон, возвращается на наинизший колебательный уровень  основного электронного состояния.При этом nл > vв, т.е. правило Стокса нарушается. Схема энергетических переходов в этом случае приведена также на рис.1, (переходы 4 и 5).
основного электронного состояния.При этом nл > vв, т.е. правило Стокса нарушается. Схема энергетических переходов в этом случае приведена также на рис.1, (переходы 4 и 5).

 :
:
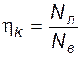

 Рис.3
Рис.3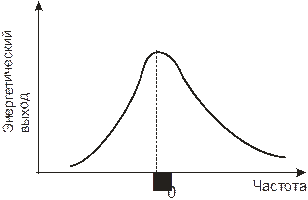 Рис.4
Рис.4 , а
, а  ,то легко установить, что энергетический и квантовый выходы люминесценции связаны соотношением:
,то легко установить, что энергетический и квантовый выходы люминесценции связаны соотношением:

 , т.е. постоянная затухания равна относительному числу возбуждённых молекул, переходящих в основное состояние, излучая фотоны люминесценции, за 1 с.
, т.е. постоянная затухания равна относительному числу возбуждённых молекул, переходящих в основное состояние, излучая фотоны люминесценции, за 1 с.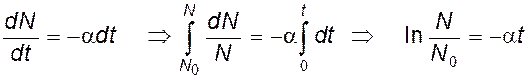

 , то из (9) нетрудно получить
, то из (9) нетрудно получить







 . Тогда
. Тогда
 , поэтому
, поэтому
 закон затухания имеет вид:
закон затухания имеет вид:

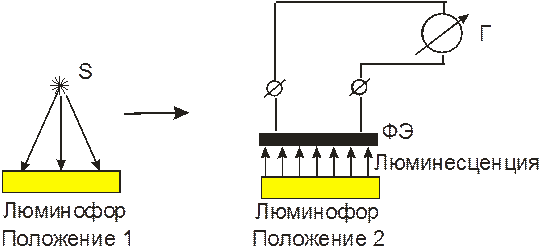 Рис.5
Рис.5
 , можно записать:
, можно записать:
 Рис.6
Рис.6
 , получим:
, получим:
 Рис.7
Рис.7