 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задание студентам для самостоятельной работы
Лабораторная работа 6 ПОСТРОЕНИЕ ВЫВОДОВ В ИСЧИСЛЕНИИ ПРЕДИКАТОВ СОДЕРЖАНИЕ ЗАНЯТИЯ Вступительная часть Исчисление предикатов, как и всякая аксиоматическая система, содержит символы (алфавит), из которых составляются формулы. Затем среди всех формул выделяются формулы, называемые выводимыми. Выделение выводимых формул в исчислении предикатов так же, как и в исчислении высказываний, осуществляется путем указания некоторой конечной совокупности формул, которые называются аксиомами, и указанием правил вывода, позволяющих из выводимых формул получать новые выводимые формулы.
Вопросы для проверки готовности студентов к занятию
1. Какие предикаты называются тождественно истинными (тождественно ложными)? 2. Сформулировать правило о введении знака отрицания под знак квантора. 3. Дать индуктивное определение формул исчисления предикатов. 4. Дать определение равносильных формул логики предикатов, выполнимых формул и общезначимых формул. 5. Сформулировать аксиомы, специфичные только для исчисления предикатов. 6. Сформулировать для исчисления предикатов основные правила вывода: правило заключения, правила введения кванторов всеобщности и существования. 7. Определить понятия вывода и доказуемых формул в исчислении предикатов.
1. Выполнимость и общезначимость формул логики предикатов
Напомним определения некоторых понятий исчисления предикатов. Каждая формула исчисления предикатов представляет собой некоторую конечную последовательность символов этого исчисления (алфавита). Алфавит исчисления предикатов можно разбить на шесть групп. 1. Малые латинские буквы с индексами или без них: a, b, c, …, x, y, z, …, a1, a2, …, x1, x2, … . Эти символы носят название переменных предметов (предметные переменные). 2. Прописные латинские буквы с индексами внизу или без них: A, B, …, A1, А2, … . Эти символы называются переменными высказываниями. 3. Прописные латинские буквы с индексами вверху: FP, GP, …, SP, …, и эти же символы с индексами внизу: 4. Знаки операций исчисления высказываний: ¯, &, Ú, ® 5. Круглые скобки: ( , ) 6. Символы кванторов " , $. Каждая формула является словом в алфавите, содержащим указанные выше в п.п. 1-6 символы. Поэтому мы определим, какие слова называются формулами. 1. Каждое переменное высказывание есть формула. 2. Если FP- символ переменного предиката, а1, а2,…, ар - символы предметных переменных, не обязательно различных, то слово FP(a1,a2,…,ap) есть формула. За такими формулами мы сохраним название переменного предиката. Формулы, определённые в п.п.1 и 2, называются элементарными. 3. Пусть формула F содержит свободную переменную х. Тогда слова "x F, $xF (1) также являются формулами. Напомним, что символы " и $, как и в алгебре предикатов, носят название кванторов: первый – квантор всеобщности, второй - квантор существования. Переменная х в формулах (1) является связанной переменной. Остальные же предметные переменные, которые формуле F свободны, остаются свободными и в обеих формулах (1). Переменные, которые связаны в формуле F, остаются связанными и в формулах (1). 4. Пусть F1 и F2 - формулы, причём в них нет таких предметных переменных, которые связаны в одной формуле и свободны в другой. Тогда слова (F1&F2), (F1Ú F2), (F1→F2), ( являются формулами. При этом свободные переменные в формулах F1 и F2 остаются свободными во всех формулах (2), а связанные переменные в формулах F1 и F2 остаются связанными и в формулах (2). Определение формулы исчисления предикатов имеет тот же индуктивный характер, что и определение формул в исчислении высказываний. Оно может быть сформулировано следующим образом: Формулой исчисления предикатов называется слово из символов алфавита этого исчисления, которое может быть построено, исходя из элементарных формул, операциями перехода от формулы F1 к формулам "xF1 и $xF1, от формул F1 и F2 к формулам (F1&F2), (F1Ú F2), (F1→F2) и Для формул исчисления предикатов можно, как и в исчислении высказываний, определить понятие подформулы. Как и в исчислении высказываний, условимся вносить некоторые упрощения в записи формул: опускать внешние скобки и некоторые внутренние, если последовательность операций, исходя из их приоритета, не вызывает сомнений; иногда круглые скобки заменяют квадратными; можно в записи Fp опускать верхний индекс р, указывающий количество переменных, если эти переменные указаны явно в формуле F. Кроме того, из условия 4 следует: а) в формуле свободные и связанные переменные должны обозначаться разными буквами; б) если какой-либо квантор находится в области действия другого квантора, то переменные, связанные этими кванторами, также обозначаются разными буквами. Для доказательства каких-либо утверждений о формулах можно применять принцип полной математической индукции по построению формул. А именно, такое доказательство имеет следующий вид. Утверждение доказывается для элементарных формул 1 и 2. Затем доказывается, что из предположения истинности этого утверждения для формулы F1следует его истинность для формул "x F и $xF, а из истинности его для формул F1 и F2 следует его истинность для формул (2). Отсюда делается заключение, что наше утверждение истинно для любой формулы. Из пунктов 1-4 определения формулы видно, что все формулы исчисления высказываний являются также формулами исчисления предикатов. Формула логики предикатов называется выполнимой в областиM, если существуют значения переменных, входящих в эту формулу и отнесенных к области M, при которых формула принимает истинные значения. Формула называется выполнимой, если существует область, на которой эта формула выполнима. Формула логики предикатов называется тождественно истинной в области М, если она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области. Формула называется общезначимой, если она тождественно истинна во всякой области. Говорят, что формула логики предикатов имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам. Среди нормальных форм логики предикатов большое значение имеют так называемые предваренные нормальные формы. В них кванторные операции либо полностью отсутствуют, либо используются после всех операций алгебры логики. Справедливо утверждение о том, что всякая формула логики предикатов путем равносильных преобразований может быть приведена к предваренной нормальной форме. При этом следует использовать равносильности логики предикатов, которые позволяют выносить за скобки кванторы существования и всеобщности, то есть равносильности вида:
Пример. Привести к предваренной нормальной форме формулу
Решение. Проводя равносильные преобразования, получим:
Задачи
1.0. Доказать, что выражение ("xF1(x)Ú"x$yG2(x,y)) является формулой, а выражение ($xF1(x)&$yG2(x,y)) формулой не является. 1.1. Выполнимы ли следующие формулы: 1.1.1. 1.1.2. 1.1.3. 1.1.4. 1.1.5. Для доказательства выполнимости той или иной формулы достаточно найти область определения соответствующих предикатов и такие их значения, что в этой области формула принимает истинные значения. Выполнимость формул 1.1.1-1.1.3 очевидна. Для доказательства выполнимости формулы 1.1.4 достаточно рассмотреть в качестве двухместного предиката Q (x, y) предикат “x делится нацело на y» на множестве N2. В формуле 1.1.5 при x = y получаем противоречие. Если же потребовать дополнительно, чтобы
1.2. Являются ли тождественно истинными следующие формулы: 1.2.1. 1.2.2. 1.2.3. 1.2.4.
Ответ: 1.2.1.Формула
представляет собой закон исключенного третьего, следовательно, эта формула общезначима. Очевидно, что 1.2.2 – тождественно ложная формула. 1.2.3. Формула
тождественно истинна, например, на множестве N2, если в качестве Q (x, y) взять отношение « Формула
1.3. Какие из нижеприведенных формул являются общезначимыми: 1.3.1. 1.3.2. 1.3.3. 1.3.4. Ответ: Используя равносильные преобразования можно доказать, что формулы 1.3.1 и 1.3.4 являются тождественно истинными на любом множестве и, следовательно, являются общезначимыми, чего нельзя сказать о формулах 1.3.2 и 1.3.3.
Привести к предваренной нормальной форме следующие формулы логики предикатов: 1.4.1. 1.4.2. 1.4.3. 1.4.4. 1.4.5. 1.4.6.
Ответ: 1.4.1. 1.4.2. 1.4.3. 1.4.4. 1.4.5. 1.4.6.
2. Вывод и доказуемость формул в исчислении предикатов
Аксиомы исчисления предикатов делятся на две группы: 1) Аксиомы исчисления высказываний, состоящих из 11 аксиом и разделенных на четыре группы I1, I2, II1 – II3, III1 – III3, IV1 – IV3 (см. лекцию № 2). 2) Две предикатные аксиомы: V1. "x F(x)→F(y). V2. F(y)→$x F(x). В аксиомах V1 и V2 F(x) – любая формула, содержащая свободные вхождения переменной x, причем ни одно из них не находится в области действия квантора по y; формула F(y) получена из F(x) заменой всех свободных вхождений переменной x на y. Напомним основные правила вывода исчисления предикатов. 1. Правило заключения (modus ponens): если G и G →H – выводимые формулы, то H – также выводимая формула. Видим, что это правило формулируется так же, как и в исчислении высказываний, только объем формул, к которым применяется это правило, здесь шире. 2. Правило введения квантора всеобщности:
где G(x) содержит свободные вхождения переменной x, а F их не содержит. 3. Правило введения квантора существования:
при тех же требованиях к формулам F и G, что и в правиле 2. Заметим, что правило подстановки окончательно исчезло из изложения; тем самым из двух возможных истолкований системы аксиом (о чем шла речь в исчислении высказываний) выбрано истолкование, при котором правило подстановки отсутствует, а вместо аксиом рассматриваются схемы аксиом. Фактически этот выбор произошел уже тогда, когда аксиомы V1 и V2 были сопровождены словесным описанием ограничений на вхождения переменных. Тем самым аксиомы перестали быть выражениями исчисления, а вместе с этим словесным текстом превратились в метаописания множества формул, являющихся аксиомами, то есть в схемы аксиом. Построение исчисления предикатов с правилом подстановки существенно более громоздко из-за необходимости различать свободные и связанные вхождения предметных переменных. Поэтому в большинстве современных книг по логике используется подход со схемами аксиом. Понятие вывода и доказуемойформулы в исчислении предикатов определяются аналогично этим понятиям в исчислении высказываний. Утверждение о том, что формула F является выводимой в исчислении предикатов, обозначается так же, как и в исчислении высказываний: ├ F. Так как все формулы, выводимые в исчислении высказываний, являются также выводимыми в исчислении предикатов, то, совершая подстановки в выводимые формулы исчисления высказываний, мы будем получать выводимые формулы исчисления предикатов.
Задачи
2.1. Доказать выводимость следующих формул в исчислении предикатов: 2.1.1. 2.1.2. F(x)→F(x) Ú "y G(y).
Решение 2.1.1. Заменяя в выводимой формуле исчисления высказываний ├ Решение 2.1.2. Заменяя в выводимой формуле ├ A→AÚ B формулу А на F(x), формулу В на "yG(y), получим ├ F(x)→F(x) Ú "yG(y). Подстановкой в выводимые формулы исчисления высказываний можно легко получить многие выводимые формулы исчисления предикатов; однако таким образом всякую выводимую формулу исчисления предикатов вывести нельзя, тем более что мы отказались от правила подстановки в исчислении предикатов, а лишь подразумеваем это правило в схемах аксиом.
2.2. Доказать следующее производное правило вывода исчисления предикатов: Если формула F(х), содержащая свободную предметную переменную х, выводима, то и формула "x F(х) также выводима в исчислении предикатов. Доказательство. Предположим, что ├ F(х). Так как для произвольной выводимой формулы G ├ A → G, то ├ А → G(х). Применяя правило связывания квантором всеобщности, получим выводимую формулу ├A→"xF(x). Можно предполагать, что А не входит в формулу F (ее всегда так можно выбрать). Заменив в последней формуле А произвольной выводимой формулой, получим ├ G →"x F(x). Применив правило заключения, получим ├"x F(x). Итак, если имеет место ├ F(х), то имеет место и ├"x F(x) и мы доказали правило, которое можно записать так:
Это правило называется производным правилом связывания квантором. Оно применимо к любой предметной переменной. В исчислении предикатов имеет место теорема, аналогичная теореме дедукции в исчислении высказываний: Если формула G выводима из формулы F, то формула F → G также выводима в исчислении предикатов. Эта теорема позволяет получать выводимые формулы исчисления предикатов, не производя для них всех операций формальной дедукции, что в значительной степени сокращает непосредственный путь вывода доказуемых формул. Отметим, что доказательства сформулированной теоремы и большинства других теорем исчисления предикатов достаточно сложны и требуют специального изучения.
2.3. Построить выводы, соответствующие следующим рассуждениям (легендам): 2.3.1. Ни один торговец наркотиками не является наркоманом. Некоторые наркоманы привлекались к ответственности. Следовательно, некоторые люди, привлекавшиеся к ответственности, не являются торговцами наркотиками. 2.3.2. Все рациональные числа являются действительными числами. Некоторые рациональные числа являются целыми числами. Следовательно, некоторые действительные числа являются целыми числами. Указание. Данные рассуждения следует формализовать (построить так называемые клаузы). Далее, используя аксиомы и правила вывода исчисления предикатов, построить вывод заключения из данных посылок, записывая последовательно все шаги доказательства.
Заключение
Содержательный смысл формул, выводимых в исчислении предикатов, показывает, что эти формулы представляют собой тождественно истинные высказывания, то есть логические тавтологии. Обратно, каждая тождественно истинная формула является выводимой в исчислении предикатов. Отсюда следует, что в исчислении предикатов нельзя вывести никакое сколько-нибудь содержательное по существу высказывание, в частности, математическое. Однако если к аксиомам исчисления предикатов присоединить какие-либо не выводимые формулы в качестве новых аксиом (сохраняя те же правила вывода), то получится другое исчисление, в котором выводимы, помимо тождественно истинных формул, и другие формулы.
Задание студентам для самостоятельной работы
1. Решить из методической разработки задачи №№1.1.2, 1.1.4, 1.2.2, 1.2.4, 1.3.2, 1.3.4, 1.4.2, 1.4.4, 1.4.6, 2.1.2, 2.2, 2.3.2. 2. Подготовиться к практическому занятию №4 «Модели теорий первопорядковой логики» по материалам лекции №6 «Метатеория формальных систем». Литература
1. Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. - СПб.: Изд-во «Лань», с. 230-234. 2. Лавров Н.А., Максимова А.А. Задачи по теории множеств, математической логике и теории алгоритмов. - М.: Наука, 1975, с. 82-98. 3. Столл Р.Р. Множества. Логика. Аксиоматические теории. – М.: Просвещение, 1968, с. 123-138.
|



 . Эти символы носят названия переменных предикатов от р переменных (р=1,2,…,n).
. Эти символы носят названия переменных предикатов от р переменных (р=1,2,…,n). )
)  (2)
(2) .
.
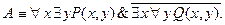




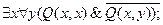

 , то в качестве P(x) можно взять предикат «квадратная матрица является невырожденной”, и тогда формула 1.1.5 становится выполнимой на множестве всех попарно различных квадратных матриц.
, то в качестве P(x) можно взять предикат «квадратная матрица является невырожденной”, и тогда формула 1.1.5 становится выполнимой на множестве всех попарно различных квадратных матриц.





 ».
». выражает рефлексивность импликации, следовательно, она тождественно истинная на любом множестве, поэтому 1.2.4 – общезначимая формула.
выражает рефлексивность импликации, следовательно, она тождественно истинная на любом множестве, поэтому 1.2.4 – общезначимая формула.



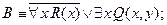

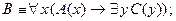








 ,
,
 ;
; А на F(x), получим выводимую формулу исчисления предикатов ├
А на F(x), получим выводимую формулу исчисления предикатов ├  .
. .
.