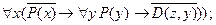ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задание студентам для самостоятельной работы
Лабораторная работа 5
ПРИМЕНЕНИЕ ЛОГИЧЕСКИХ И КВАНТОРНЫХ ОПЕРАЦИЙ НАД ПРЕДИКАТАМИ СОДЕРЖАНИЕ ЗАНЯТИЯ Вступительная часть Язык логики предикатов является расширением языка логики высказываний. По этой причине расширяется и алфавит, и набор операций. Формулы логики предикатов получают определенную интерпретацию, если указано непустое множество М и заданы истинностные значения каждого из входящих в формулу компонентов. Особый интерес представляют общезначимые формулы (тождества, логические законы), истинностное значение которых равно 1 в любой интерпретации. Поэтому студентам необходимо овладеть достаточно богатым запасом тождеств логики предикатов и уметь их обосновывать при помощи содержательных теоретико-множественных соображений. На практическом занятии рекомендуется решить задачи №№1.1.1, 1.1.3, 1.1.4, 1.1.5, 1.1.7, 1.2.1, 1.2.4, 1.3.1, 1.3.3, 2.1.1-2.1.8, 2.2.1, 2.3.1, 2.3.3, 2.3.5, 2.4.2, 2.4.4, 3.1.1, 3.2.1, 3.2.3, 3.2.5, 3.2.7, 3.2.9, 3.2.11, 3.3.1, 3.3.3, 3.3.5.
Вопросы для проверки готовности студентов к занятию
1. Что является отличительной особенностью логики предикатов от логики высказываний? 2. Что представляет собой высказывательная форма? 3. Дать определение одноместного предиката, его области определения и множества истинности. 4. Какие предикаты называются тождественно истинными (тождественно ложными)? 5. Каким образом понятие одноместного предиката обобщается на понятие многоместного предиката? 6. Дать определение логических операций над предикатами. Как связаны результаты логических операций над предикатами с множествами истинности исходных предикатов? 7. Дать определение кванторных операций. 8. Сформулировать правило о введении знака отрицания под знак квантора. 9. Дать определение формулы и подформулы логики предикатов. 10. Дать определение равносильных формул логики предикатов.
Содержание занятия
1. Нахождение областей истинности предикатов
Конъюнкцией одноместных предикатов P(x) и Q(x) называется предикат P(x)&Q(x), который обращается в истинное высказывание тогда и только тогда, когда в истинное высказывание обращается каждый из предикатов P(x) и Q(x). Если JP, JQ, JP&Q – области истинности предикатов P(x), Q(x) и P(x)&Q(x) соответственно, то Дизъюнкцией предикатов P(x) и Q(x) называется предикат Область истинности Отрицанием предиката P(x) , заданного на множестве М, называется предикат Если JP – область истинности предиката P(x), Импликацией предикатов P(x) и Q(x), заданных на множестве М, называется предикат Областью истинности предиката Определения конъюнкции, дизъюнкции, отрицания и импликации можно обобщить и на случай многоместных предикатов.
Задачи
1.1. На множестве М= A (x) B (x) С (x) D (x) Найти области истинности следующих предикатов: 1.1.1. A(x)&B(x); 1.1.2. B(x)&C(x); 1.1.3. B(x) 1.1.4. 1.1.5. С(x) 1.1.6. 1.1.7. 1.1.8. Ответы: 1.1.1. 1.1.2. 1.1.3. 1.1.5. 1.1.6. 1.1.7. 1.1.8.
1.2. Изобразить на диаграммах Эйлера-Венна области истинности для следующих предикатов: 1.2.1. 1.2.2. 1.2.3. 1.2.4. Ответы: 1.2.1.
M
1.2.2. Закрашенная часть множества M:
1.2.3. 1.2.4.
.
1.3. Изобразить на координатной плоскости области истинности предикатов (Mx = My = R): 1.3.1. 1.3.2. 1.3.3. 1.3.4. Решим, например, задачу 1.3.4. Очень часто в математике конъюнкцию уравнений и неравенств записывают в виде системы. Запишем нашу систему неравенств в виде конъюнкции предикатов:
y=1/3x+2 B
0 C
Получается заштрихованный треугольник АВС.
Квантор всеобщности. Пусть P(x) – предикат, определенный на множестве М. Тогда под выражением Квантор существования. Под выражением $xP(x) понимают высказывание, которое является истинным в том и только в том случае, когда существует элемент Переменную x в предикате P(x) называют свободной, а в выражениях
2. Доказательство равносильности формул логики предикатов
Предикатные символы от предметных постоянных и переменных и переменные высказывания называются элементарными формулами. Из элементарных формул с помощью операций &,
2.1. Какие из следующих выражений (слов) являются формулами логики предикатов? В каждой формуле выделить свободные и связанные переменные. 2.1.1. 2.1.2 2.1.3 2.1.4. 2.1.5. 2.1.6. 2.1.7. 2.1.8. Решение. Формулами являются 2.1.1, 2.1.2, 2.1.3, 2.1.6 и 2.1.7. Остальные выражения формулами не являются. В формуле 2.1.1. y – свободная переменная, x и z - связанные переменные; в формуле 2.1.2 y – свободная переменная, x – связанная; в формуле 2.1.3 нет предметных переменных; в формуле 2.1.6 y – свободная переменная, x и z – связанные; в формуле 2.1.7 – y – свободная переменная, x – связанная. Выражение 2.1.4 не является формулой, так как операция конъюнкции применена к формулам P(x) и
2.2. Вычислить значения формул: 2.2.1. 2.2.2. где P(x) Ответ: в случае 2.2.1 данная формула принимает значение «истина»; формула 2.2.2 принимает значение «ложь». Во втором случае высказывание 2.3. Доказать следующие равносильности: 2.3.1. 2.3.2. 2.3.3. 2.3.4. 2.3.5. 2.3.6.
В качестве примера докажем равносильность предикатов в 2.3.3. Рассмотрим два случая. а) Пусть высказывание с – ложно. Тогда для любого x ложными будут высказывания б) Пусть теперь высказывание с истинно. Тогда, очевидно, значения исходных формул будут целиком зависеть от значений предиката A(x). Если A(x) – тождественно истинный предикат, то будет тождественно истинным и предикат
2.4. Найти отрицания следующих формул: 2.4.1. 2.4.2. 2.4.3. 2.4.4. 2.4.5. Решим, например, 2.4.2 и 2.4.3.
2.4.2.
2.4.3. Мы воспользовались правилом введения отрицания под знак квантора.
2.5. Пусть A(x) и B(x) – два одноместных предиката, определенных на множестве М таких, что высказывание Доказательство легко проводится методом от противного.
3. Применениелогики предикатов для записи математических Определений и предложений
3.1. Записать на языке логики предикатов определения: 3.1.1. Линейно упорядоченного множества (множество называется линейно упорядоченным, если для любых элементов этого множества x и y либо x=y, либо x < y, либо x > y). 3.1.2. Ограниченной функции (функция f(x) называется ограниченной на множестве М, если существует такое неотрицательное число l, что для всех x Ответ: 3.1.1. 3.1.2. 3.2. Записать на языке логики предикатов следующие высказывания: 3.2.1. Некоторые действительные числа являются рациональными. 3.2.2. Ни одно простое число не является точным квадратом. 3.2.3. Некоторые четные числа не делятся на 8. 3.2.4. Всякое число, кратное 6, делится на 3. 3.2.5. Числа 5 и 12 не имеют общих делителей, отличных от +1 и –1. 3.2.6. Натуральное число, делящееся на 6, делится на 2 и на 3. 3.2.7. Для любого целого числа x существует такое целое число y, что x = 2y или x = 2y+1. 3.2.8. Для любого натурального числа существует другое натуральное число, которое больше первого. 3.2.9. Существует наименьшее натуральное число. 3.2. 10. Не существует такого рационального числа x, что x2 – 2 = 0. 3.2.11. Для всяких целых чисел x и z существует целое число y такое, что x + y = z. 3.2.12. Для любых двух рациональных чисел x и y существует рациональное число z такое, что x< z и z < y. 3.3. Пусть P(x) обозначает «x – простое число», Q(x) – «x – четное число», R(x) – «x – целое число», D(x, y) – «x делит y». Сформулировать словами следующие высказывания, записанные на языке логики предикатов. Отметить, какие из них истинные и какие ложные: 3.3.1. 3.3.2. 3.3.3. 3.3.4. 3.3.5. 3.3.6.
Заключение
В результате изучения и исследования цикла задач на логику предикатов, мы фактически совершаем переход на новый уровень абстракции такого типа, какой был совершен в школе – от арифметики вещественных чисел к алгебре числовых функций. Новым здесь по сравнению с алгеброй высказываний и исчислением высказываний является введение кванторных операций. Эти операции широко используются для записи определений и компактной записи доказательства различных теорем
Задание студентам для самостоятельной работы
1. Решить из методической разработки задачи №№1.1.2, 1.1.6, 1.1.8, 1.2.2, 1.2.3, 1.3.2, 1.3.4, 2.2.2, 2.3.2, 2.3.4, 2.3.6, 2.4.1, 2.4.3, 2.4.5, 2.5, 3.1.2, 3.2.2, 3.2.4, 3.2.6, 3.2.8, 3.2.10, 3.2.12, 3.3.2, 3.3.4, 3.3.6. 2. Подготовиться к практическому занятию №3 «Построение выводов в исчислении предикатов». Литература
1. Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. - СПб.: Изд-во «Лань», с. 214-240. 2. Лавров Н.А., Максимова А.А. Задачи по теории множеств, математической логике и теории алгоритмов. - М.: Наука, 1975, с. 75-90. 3. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения. - М.: Вузовская книга, 1998, с. 245-246. 4. Акимов О.Е. Дискретная математика: логика, группы, графы. - М.: Лаборатория Базовых Знаний, 2001, с. 65-95.
|



 .
. который обращается в истинное высказывание для тех и только тех значений переменной x из области определения данных предикатов, для которых хотя бы один из предикатов P(x) или Q(x) обращается в истинное высказывание.
который обращается в истинное высказывание для тех и только тех значений переменной x из области определения данных предикатов, для которых хотя бы один из предикатов P(x) или Q(x) обращается в истинное высказывание. дизъюнкции
дизъюнкции  является множество
является множество  .
. , который обращается в истинное высказывание для тех и только тех значений
, который обращается в истинное высказывание для тех и только тех значений  , для которых предикат P(x) обращается в ложное высказывание.
, для которых предикат P(x) обращается в ложное высказывание.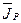 - дополнение множества JP до множества М, то областью истинности предиката
- дополнение множества JP до множества М, то областью истинности предиката  \ JP.
\ JP. , который обращается в ложное высказывание для тех и только значений
, который обращается в ложное высказывание для тех и только значений 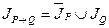 .
. заданы предикаты:
заданы предикаты: ”x не делится на 5”;
”x не делится на 5”;
 ;
; ;
; A(x);
A(x); ;
; ;
; .
. ;
; ;
; ;
; 









 - закрашенная часть множества M.
- закрашенная часть множества M.




 M
M

 то есть данный предикат является тождественно истинным на любом множестве.
то есть данный предикат является тождественно истинным на любом множестве.
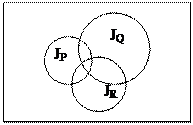
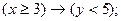




 Тогда
Тогда  Мы имеем пересечение трех полуплоскостей с границами, определяемых уравнениями
Мы имеем пересечение трех полуплоскостей с границами, определяемых уравнениями 



 Y
Y y=-1/2x+3 y=2x-4
y=-1/2x+3 y=2x-4 A X
A X понимают высказывание истинное, когда предикат P(x) обращается в истинное высказывание для каждого элемента
понимают высказывание истинное, когда предикат P(x) обращается в истинное высказывание для каждого элемента  и в ложное - в противном случае.
и в ложное - в противном случае.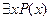 - связанной. Кванторы
- связанной. Кванторы  и
и  называютсядвойственными друг другу. Знак отрицания можно ввести под знак квантора, заменив квантор двойственным ему квантором.
называютсядвойственными друг другу. Знак отрицания можно ввести под знак квантора, заменив квантор двойственным ему квантором. можно получать более сложные формулы логики предикатов.
можно получать более сложные формулы логики предикатов.

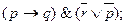





 в первой из них переменная x – свободная, во второй – связана квантором всеобщности, что противоречит определению формулы; в выражении 2.1.5 квантор существования по переменной y навешен на формулу
в первой из них переменная x – свободная, во второй – связана квантором всеобщности, что противоречит определению формулы; в выражении 2.1.5 квантор существования по переменной y навешен на формулу  , в которой переменная y связана квантором всеобщности, что также противоречит определению формулы; наконец, выражение 2.1.8 не является формулой, так как переменная y не связана квантором.
, в которой переменная y связана квантором всеобщности, что также противоречит определению формулы; наконец, выражение 2.1.8 не является формулой, так как переменная y не связана квантором.

 - истинно, а высказывание
- истинно, а высказывание  - ложно, следовательно, вся формула принимает значение «ложь» по определению импликации высказываний.
- ложно, следовательно, вся формула принимает значение «ложь» по определению импликации высказываний.

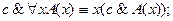

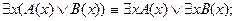

 и
и 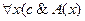 . Следовательно, в этом случае обе исходные формулы тождественно ложны.
. Следовательно, в этом случае обе исходные формулы тождественно ложны. , и, следовательно, будут тождественно истинными высказывания
, и, следовательно, будут тождественно истинными высказывания  ,
,  , то есть тождественно истинны исходные формулы. Если же предикат не тождественно истинный. Тогда будет не тождественно истинным предикат
, то есть тождественно истинны исходные формулы. Если же предикат не тождественно истинный. Тогда будет не тождественно истинным предикат 

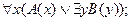



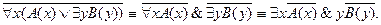

 истинно. Доказать, что высказывание
истинно. Доказать, что высказывание  M справедливо неравенство
M справедливо неравенство 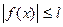 ).
).