 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Система аксиом исчисления высказываний
Лабораторная работа № 4 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ К ТЕОРИИ ДОКАЗАТЕЛЬСТВ
СОДЕРЖАНИЕ ЗАНЯТИЯ Вступительная часть Исчисление высказываний – это одна из аксиоматических логических систем, интерпретацией которой является алгебра высказываний. Эта теория строится без использования понятий истинности и ложности, без применения законов логики высказываний. Исчисление высказываний строится по общим правилам построения формальных аксиоматических систем. Доказуемость формул исчисления высказываний основывается на его аксиомах, основных и производных правилах вывода. Поэтому важное значение приобретает усвоение на практике правил вывода и, прежде всего, правила заключения и правила подстановки. Второй важной составной частью исчисления высказываний является умение для различных формул строить вывод и устанавливать выводимость формул из совокупности формул. Особое значение для исчисления высказываний имеет теорема дедукции, которая служит обоснованием важного приема доказательства теорем, исчисления высказываний с одной стороны, а с другой – в модулированном виде она используется и в других исчислениях. На занятии рекомендуется решить задачи №№1.1.1.1 – 1.1.1.8, 1.1.2.4, 1.2.2, 1.2.4, 1.3.1.1, 1.3.1.4, 1.3.2.1, 1.3.2.2, 2.1.1, 2.1.4, 2.2.
Вопросы для проверки готовности студентов к занятию
1. Сформулировать основные принципы построения формальной теории (исчисления). 2. Из чего состоит алфавит исчисления высказываний? 3. Дать индуктивное определение формулы исчисления высказываний. 4. Дать определение подформулы данной формулы. 5. Записать систему аксиом исчисления высказываний. Что такое схема аксиом? 6. Сформулировать основные правила вывода исчисления высказываний (правило заключения и правило подстановки). 7. Дать определение выводимой формулы, теоремы. 8. Что такое производные правила вывода. Сформулировать несколько таких правил. 9. Понятие вывода из совокупности формул – это определение или теорема? 10. Сформулировать теорему дедукции. 11. Какими теоремами выражается связь между алгеброй высказываний и исчислением высказываний?
1. Доказуемость формул
1.1. Определение формулы и подформулы исчисления высказываний Определение формулы: 1. Всякая переменная x, y, z,… является формулой. 2. Если А и В – формулы, то формулами являются и следующие комбинации символов: (A&B), 3. Никакая другая комбинация символов формулой не является.
Определение подформулы: 1. Подформулой переменного высказывания x, y, … является только эта переменная. 2. Если формула имеет вид 3. Если формула имеет один из видов
Задача 1.1.1. Какие из следующих выражений являются формулами исчисления высказываний: 1.1.1.1. 1.1.1.2. 1.1.1.3. 1.1.1.4. 1.1.1.5. 1.1.1.6. 1.1.1.7. 1.1.1.8.
Ответ: выражения 1.1.1.2, 1.1.1.5 и 1.1.1.8 формулами не являются.
Задача 1.1.2. Выписать все подформулы формул: 1.1.2.1. 1.1.2.2. 1.1.2.3. 1.1.2.4. 1.1.2.5. 1.1.2.6. Выпишем, например, все подформулы формулы 1.1.2.4:
1.2. Система аксиом и основные правила вывода исчисления высказываний Система аксиом исчисления высказываний Первая группа аксиом:
I1. I2.
Вторая группа аксиом:
II1. II2. II3.
Третья группа аксиом:
III1. III2. III3.
Четвертая группа аксиом:
IV1. IV2. IV3.
Правило заключения (modus ponens):
на языке доказуемых формул.
Правило подстановки:
Определение доказуемой формулы: 1. Каждая аксиома является доказуемой формулой. 2. Формула, полученная из доказуемой формулы путем применения основных правил вывода, доказуема. 3. Никакая другая формула исчисления высказываний доказуемой не является.
Установление доказуемости той или иной формулы исчисления высказываний часто требует использования обобщения правила заключения – правила сложного заключения:
Задача 1.2. Установить доказуемость формул: 1.2.1. 1.2.3. 1.2.4. 1.2.5.
Решение 1.2.1. В аксиоме III1 осуществим подстановку вместо x Решение 1.2.2. К доказуемости приводит постановка в аксиому I2 вместо x, y, z соответственно формул Решение 1.2.3. В аксиоме III3 сделаем подстановку вместо x, y, z формулы А. Получим доказуемую формулу
Решение 1.2.4. В аксиоме II3 осуществим подстановку вместо x, y, z соответственно B, A, Решение 1.2.5. В аксиоме III3 следует осуществить подстановку вместо x, y, z соответственно A, B,
1.3. Производные правила вывода
Задача 1.3.1. Доказать следующие производные правила вывода: 1.3.1.1.Правило силлогизма. 1.3.1.2. 1.3.1.3. 1.3.1.4. 1.3.1.5. 1.3.1.6.
Решение 1.3.1.1. В аксиоме I1 сделаем подстановку вместо x, y соответственно формул
Решение 1.3.1.2. По условию | | а по правилу заключения и из условия получаем окончательно | Решение 1.3.1.3. Используем аксиому II1:
Решение 1.3.1.5. Элементарно. Указание к решению 1.3.1.6. Воспользоваться доказуемой формулой Задача 1.3.2. Используя производные правила вывода показать, что доказуемы следующие формулы: 1.3.2.1. 1.3.2.2. 1.3.2.3.
Из аксиом II1 и II2 получим:
К (2) и (3) применим правило контрапозиции:
Из (1), (4), (5) по правилу сложного заключения получаем доказуемость формулы 1.3.2.1. Решение 1.3.2.2. В аксиоме I2 сделаем подстановку вместо x, y, z соответственно
В аксиоме II2 сделаем подстановку вместо x, y соответственно
где (3) – правило контрапозиции. В аксиоме II1 сделаем подстановку вместо x, y соответственно
Из (3) и (4) получим
Из (1), (2), (5) по правилу сложного заключения получим | Решение 1.3.2.3. В аксиоме III3 сделаем подстановку, заменяя в ней z на
Из аксиом II1 и II2 имеем :
Используя правило контрапозиции к (2) и (3) получим:
Используя правило снятия двойного отрицания, получим:
Применяя к формуле (8) правило контрапозиции, а затем правило снятия двойного отрицания, получим последовательно:
2. Построение выводов Выводом формулы В из совокупности формул Г={А1, А2, …, Аn} называется последовательность формул F1, F2,…, Fm такая, что Fm=B, а любая из формул F1, F2,…, Fm является либо аксиомой, либо одной из исходных формул А1, А2, …, Аn, либо непосредственно выводима из формул, предшествующих ей в последовательности F1, F2,…, Fm по правилам вывода.
А1, А2, …, Аn называются гипотезами или посылками вывода.
Задача 2.1. Записать вывод для следующих формул: 2.1.1. 2.1.2. Г= 2.1.3. Г= 2.1.4. Н=
Решение 2.1.1. Запишем последовательность формул F1, F2,…, Fm, то есть вывод из Н:
Решение 2.1.2.
Решение 2.1.3.
Решение 2.1.4.
Доказательство. По правилу силлогизма
Обозначим через Г1 = Заключение Рассмотренные нами на практическом занятии задачи, относящиеся к исчислению высказываний, позволяют овладеть отдельными логическими правилами вывода для доказательства формул и построения выводов для различных формул.
Использованная при подготовке к занятию литература 1. Лихтарников Л.М., Сукачева Т.Г. Математическая логика/Курс лекций.- СПб.: Изд-во «Лань», 1998, с. 204-213. 2. Лавров Н.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Наука, 1975, с. 64-74.
|





 .
.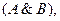





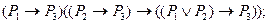



 ;
; ;
; ;
;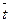 ;
;

 , x&y,
, x&y,  x1y;
x1y;  подформулой не является, поскольку операция
подформулой не является, поскольку операция  слабее операции &).
слабее операции &).

 ;
;
 ;
; ;
;
 ;
; ;
;

 или
или 




 Это правило мы тоже будем относить к основным, поскольку оно легко получается последовательным применением правила заключения. Действительно, так как ├А1 и ├
Это правило мы тоже будем относить к основным, поскольку оно легко получается последовательным применением правила заключения. Действительно, так как ├А1 и ├  то доказуемой будет и формула
то доказуемой будет и формула  ; из │
; из │  и │
и │  следует │
следует │  и так далее. На последнем шаге ввиду конечности формул А1, А2, …, An, получим │
и так далее. На последнем шаге ввиду конечности формул А1, А2, …, An, получим │ 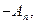 │
│  и, следовательно │
и, следовательно │ 
 ; 1.2.2.
; 1.2.2. 
 ;
;

 , вместо y – C.
, вместо y – C.

 Как было доказано на лекции №3,
Как было доказано на лекции №3,  Поэтому, применяя правило сложного заключения, получим
Поэтому, применяя правило сложного заключения, получим 
 Получим
Получим  Снова применяя правило сложного заключения, получим доказуемость формулы 1.2.4.
Снова применяя правило сложного заключения, получим доказуемость формулы 1.2.4.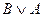 , и воспользоваться правилом сложного заключения.
, и воспользоваться правилом сложного заключения.


 Производные правила вывода получаются с помощью правил заключения и подстановки и позволяют получать новые доказуемые формулы. На лекции №3 были приведены некоторые такие правила: правило одновременной подстановки, рассмотренное уже в предыдущем пункте правило сложного заключения, правило силлогизма
Производные правила вывода получаются с помощью правил заключения и подстановки и позволяют получать новые доказуемые формулы. На лекции №3 были приведены некоторые такие правила: правило одновременной подстановки, рассмотренное уже в предыдущем пункте правило сложного заключения, правило силлогизма  правило контрапозиции
правило контрапозиции  правила снятия двойного отрицания
правила снятия двойного отрицания  и
и  При этом на лекции было доказано правило контрапозиции, а правила снятия двойного отрицания надо было доказать самостоятельно.
При этом на лекции было доказано правило контрапозиции, а правила снятия двойного отрицания надо было доказать самостоятельно.


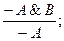




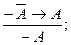

 ;
; и А, а в аксиоме I2 вместо x, y, z подставим формулы А, В и С соответственно. Получим доказуемые формулы:
и А, а в аксиоме I2 вместо x, y, z подставим формулы А, В и С соответственно. Получим доказуемые формулы:
 (1)
(1) (2)
(2) Так как по условию доказуемы формулы
Так как по условию доказуемы формулы  и
и  . По правилу заключения из формулы (1) получаем
. По правилу заключения из формулы (1) получаем
 , (3)
, (3)
 .
. а из аксиомы II1 имеем |
а из аксиомы II1 имеем |  Применим к последней формуле правило контрапозиции:
Применим к последней формуле правило контрапозиции:


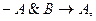
 Так как по условию
Так как по условию  , то по правилу заключения получим
, то по правилу заключения получим  .
. Решение 1.3.1.4. По условию │
Решение 1.3.1.4. По условию │  , │
, │  Тогда легко показать │
Тогда легко показать │  и затем |
и затем |  . Остается применить правило заключения.
. Остается применить правило заключения.


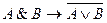 .
. Решение 1.3.2.1. В аксиоме III3 вместо x, y, z подставим соответственно
Решение 1.3.2.1. В аксиоме III3 вместо x, y, z подставим соответственно  Получим
Получим  (1)
(1)
 (2)
(2) . (3)
. (3)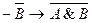 . (5)
. (5)
 :
:
 (1)
(1) и
и  :
: (2)
(2)
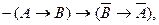 (3)
(3)
 . (4)
. (4) (5)
(5)
 :
:
 или
или . (1)
. (1)
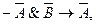



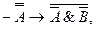 (4)
(4) (5).
(5).
 , (6)
, (6)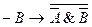 (7).
(7). (8).
(8).
 ,
, Если существует вывод формулы В из совокупности формул Г, то говорят, что формула В выводима из Г и записывают Г
Если существует вывод формулы В из совокупности формул Г, то говорят, что формула В выводима из Г и записывают Г  или А1, А2, …, Аn
или А1, А2, …, Аn  Н=
Н=  , Н
, Н  Г
Г  Г
Г  , Н
, Н  .
. (подстановка в аксиому II3 вместо x, y, z соответственно А, В, А);
(подстановка в аксиому II3 вместо x, y, z соответственно А, В, А); (как доказуемая формула);
(как доказуемая формула);  (по правилу заключения из F3 и F4;
(по правилу заключения из F3 и F4;  (подстановка в I1 вместо x, y соответственно В и А);
(подстановка в I1 вместо x, y соответственно В и А);  (по правилу заключения из F2 и F6);
(по правилу заключения из F2 и F6);  (по правилу заключения из F5 и F7);
(по правилу заключения из F5 и F7);  (по правилу заключения из F1 и F8).
(по правилу заключения из F1 и F8).

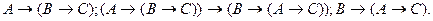
 , то Г
, то Г 

 .
. . Тогда Г1|
. Тогда Г1|  По теореме дедукции, которая имеет вид
По теореме дедукции, которая имеет вид  , получим Г |
, получим Г |  .
.