 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ЛАБОРАТОРНАЯ РАБОТА № 4 – 6
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА С ПОМОЩЬЮ МАГНЕТРОНА
Целью настоящей работы является экспериментальное определение заряда электрона методом отклонения движущихся электронов в магнитном поле.
В В Е Д Е Н И Е
Одной из главных характеристик заряженной частицы, как и всякого заряженного тела, является электрический заряд q . Однако движение заряженной частицы в электрическом и магнитном полях определяется не зарядом q , а отношением заряда q к массе m частицы, называемым удельным зарядом. Поясним это на некоторых примерах: 1. Пусть частица с зарядом q движется в электрическом поле напряженности Запишем для такой частицы уравнение движения:
Нетрудно видеть, что ускорение заряженной частицы в электрическом поле зависит от ее удельного заряда:
2. Пройдя разность потенциалов U , заряженная частица приобретает энергию, равную величине:
Из этого равенства следует, что другая характеристика частицы - ее скорость также определяется удельным зарядом: V = (2qU/m)1/2 (2) 3. Если заряженная частица, движущаяся по инерции, попала в магнитное поле со скоростью
В соответствии с правилами векторного умножения направление силы Изменяется лишь направление скорости, а это означает, что заряженная частица в однородном магнитном поле должна двигаться точно по окружности, если нет составляющей скорости V вдоль магнитного поля. Таким образом, сила Лоренца выступает в качестве центростремительной силы (см.рис.1и 2) .
откуда можно найти радиус траектории
Таким образом, радиус траектории движения заряженной частицы в магнитном поле определяется также значением удельного заряда частицы q/ m. Если (V/C)2 << 1, где С - скорость света, то потерями энергии частицы в результате излучения при движении с ускорением можно пренебречь.
Рис.1. Траектория положительно заряженной частицы, попавшей в однородное поле Рис.2. Примерные траектории протона и электрона в однородном поле (частицы образовались в поле при распаде нейтрона).
Рассмотренные примеры показывают, что разные частицы, но с одинаковым удельным зарядом будут двигаться в электрическом и магнитном полях совершенно одинаково. Этим и определяется важное значение величины удельного заряда. В истории физики опытное определение удельного заряда сыграло очень важную роль, т.к. оно предшествовало определению заряда и массы частиц и сделало возможным это определение. Дело в том, что ни уравнение (2) , относящееся к движению частиц в электрическом поле, ни уравнение (3), описывающее движение частиц в магнитном поле, не позволяет определить заряд и массу частиц порознь, т.к. в каждом из этих уравнений содержится три неизвестных величины V , q , m. По той же причине заряд и масса не могут быть определены и при совместном решении обоих уравнений. Но если определять не q и m в отдельности, а их отношение, т.е. удельный заряд, то оба уравнения содержат лишь два неизвестных q/m и V и поэтому их совместное решение возможно. На этом и основано большинство методов экспериментального определения удельного заряда частиц. Для этого исследуется движение частиц одновременно в электрическом и магнитном полях, так чтобы можно было использовать уравнения (2) и (3) . Непосредственно тем или иным способом могут быть определены разность потенциалов электрического поля, напряженность магнитного поля и радиус окружности, по которой частица движется в магнитном поле. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Исследуемыми частицами в данной работе являются электроны (заряд электрона в дальнейшем будем обозначать буквой ℓ). Электроны можно “получить” с помощью явления термоэлектронной эмиссии, которое заключается в том, что раскаленная металлическая нить, помещенная в вакуум, испускает со своей поверхности заряженные частицы (термоэлектроны). В качестве источника электронов в настоящей работе используется подогревный катод электронной лампы. Магнитное поле, в которое помещается электронная лампа, создается соленоидом, магнитная индукция которого находится по формуле:
B - индукция магнитного поля внутри соленоида, m=1, m0=4p * 10-7 Гн/м, N - число витков соленоида, I - сила тока , L - длина соленоида, D - диаметр соленоида. Электронная лампа помещается в соленоид таким образом, чтобы магнитные силовые линии были параллельны оси катода лампы. В качестве электронной лампы в настоящей работе можно использовать трехэлектродную лампу (а также четырех - либо пятиэлектродную), сетка “С” в которой соединена с анодом “А” (см. Рис.3) .
Рис.3. Рис.4. При таком соединении электрическое поле между сеткой и анодом близко к нулю (т.к. разность потенциалов между сеткой и анодом равна нулю). Следовательно, электроны ускоряются только в пространстве между катодом К и сеткой, двигаясь дальше к аноду с постоянной скоростью, которая определяется выражением (2) . U в этом случае - разность потенциалов между сеткой и катодом. Если магнитное поле отсутствует, то частицы двигаются по радиусу системы (рис.4 , пунктирная линия). В слабом магнитном поле траектория частиц под действием силы Лоренца искривляется (кривая 1, рис. 4) . Причем, в промежутке между сеткой и анодом, где электрическое поле отсутствует, электроны, согласно сказанному выше, должны двигаться точно по окружности. В промежутке между катодом и сеткой радиус кривизны будет переменным, т.к. скорость электронов изменяется под действием электрического поля. Радиус окружности в промежутке между сеткой и анодом будет определяться величиной магнитного поля (выражение (3)) . Из этого же выражения следует, что если радиус r значительно меньше половины радиуса анода, то электроны не достигнут анода (рис.4, траектория 3) . Не достигнут анода и те электроны, радиус кривизны траектории которых r £ Ra/2, если радиусы катода и сетки малы по сравнению с радиусом анода. Решая совместно (2) и (3) , получим следующее соотношение для удельного заряда электрона:
Формула (5) позволяет вычислить ℓ /m, если при заданном U найдено такое значение магнитного поля (или, наоборот, при заданном В такое значение U) , при котором электроны перестают попадать на анод. Это означает, что ток в цепи анода отсутствует (рис.5), а значение магнитного поля в этом случае называют критическим. С учетом сказанного, выражение (4) и (5) будут иметь вид:
откуда окончательно:
До сих пор предполагалось, что все электроны покидают катод со скоростью точно равной нулю. Как следует из (6) в этом случае при I< Iкр все электроны без исключения попадали бы на анод, а при I> Iкр все возвращались бы на катод, не достигнув анода. Анодный ток Ia с увеличением тока в соленоиде Ic (а равно и магнитного поля) изменялся бы так, как это изображено на рис.5 пунктирной прямой а-а.
Рис.5. Рис.6. На самом деле электроны, испускаемые нагретым катодом, обладают различными начальными скоростями. Поэтому для различных электронов критические условия достигаются при различных значениях Ic (пунктирная линия a-b) и лишь те электроны, у которых начальная скорость равна нулю, не достигнут анода при значении Ic в точке а. Критический ток в соленоиде для самых быстрых электронов будет соответствовать точке b. Для расчетов мы должны были бы брать значение Iкр, соответствующее точке а, поскольку формула (6) справедлива для электронов с начальной скоростью на выходе из катода точно равной нулю. Однако это верно, когда исключены все другие возможные возмущения, способные изменить ход кривой а - b. В действительности, например, некоторая несносность катода и анода приводит к тому, что часть электронов не достигнет анода при меньших значениях, чем Iкр, соответствующее точке а (см. рис. 5 и 6) . Отклонение магнитного поля от перпендикулярности электрическому полю, некоторый пространственный заряд, создаваемый электронами в объеме между катодом и сеткой и т.д. приводят к тому, что зависимость Ia от Ic представляется кривой f-d (рис.7.). За Iкр принимается некоторое среднее значение Ic , лежащее между точками f и d. Для большей определенности удобно брать значение Iкр, соответствующее точке участка f-d, где | (ΔIa) / (ΔIa) | достигает максимума, (см. рис.8), т.е., где наблюдается наибольший излом кривой f-d.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
1. В качестве электронной лампы в данной работе используется лампа 6Ф6С, управляющая и экранная сетка которой во внешней цепи соединены накоротко с анодом. Cхема установки представлена на рис.3. Схема включения соленоида на рис.9. Включить установку в сеть.
Рис.9. 2. При помощи реостата, с которого подается напряжение на лампу, устанавливают разность потенциалов U между сеткой и катодом порядка 4-8 В (по указанию преподавателя). Когда анодный ток примет стабильную величину, в таблицу 1 заносят первое показание Ia , соответствующее Ic = 0. Таблица 1
Затем плавно, через равные интервалы подают ток в обмотку соленоида и снимают показания анодного тока в зависимости от тока в соленоиде, причем, дважды; в прямой последовательности, когда ток в соленоиде возрастает и обратной, через те же значения тока в соленоиде, когда ток в соленоиде уменьшается. Результаты измерений заносят в таблицу 1. Рассчитывают средние значения анодного тока
приращения ΔIаср, ΔIс и отношение 3. На основании данных таблицы 1 вычерчивают на миллиметровой бумаге 2 кривые. Первая дает зависимость Iaср = f1(Iс). Вторая кривая - зависимость | ΔIaср /Δ Ic | = f2(Ic) (см. рис.7 и 8). Максимальному значению | ΔIaср / ΔIc | соответствует критический ток Iкр соленоида. 4. Для расчета искомой величины необходимо знать “параметры” катушки соленоида и анодного цилиндра. Эти данные указаны в табличке, приклеенной на установке. Их необходимо свести в таблицу 2 , куда заносятся также значения Iкр и разность потенциалов U . Таблица 2
5. По формуле (6) рассчитать удельный заряд электрона. 6. Сравнить полученный результат с табличным значениям
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Что такое сила Лоренца? Как определяется ее величина и направление? 2. Покажите, что магнитное поле не совершает работы над заряженной частицей. 3. Какой “толщины” должна быть область магнитного поля на поверхности Земли, чтобы протон с энергией 1МэВ не долетел до поверхности Земли? 4. Выведите расчетную формулу для определения ℓ/m. 5. Почему анодный ток плавно изменяется с возрастанием тока в соленоиде? 6. При каких условиях анодный ток упадет до нуля скачком? 7. При каком характере зависимости Ia от Ic достигается наибольшая точность определения удельного заряда электрона?
Л И Т Е Р А Т У Р А
1. Савельев И.В. Курс общей физики т.2 1978г.
|
. Сила, действующая на частицу в поле, равна, очевидно, q 
(1)
, то на неё со стороны поля действует сила Лоренца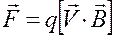
перпендикулярно как скорости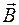 
. Следовательно, элементарная работа по перемещению заряда q в поле 
, т.е. значение кинетической энергии (mV2)/2 частицы в магнитном поле сохраняется, и сохраняется численное значение (модуль) скорости 
.
(3)
, (4)
(5)
(6)
Из рисунка 7 ясно также, что чем меньше (Id - If) по отношению к Iа, тем точнее можно определить значение ℓ/m, т.к. именно в этом случае любое значение Ia, лежащее в промежутке If и Id, будет отличаться друг от друга на малую величину.
,
.
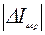
. Сделать вывод.