 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Решение и геометрическая интерпретация игровых моделей размера 2 x 2, 2 x n, m x 2
ЛАБОРАТОРНАЯ РАБОТА 4
В решении игр используется следующая теорема: если один из игроков применяет свою оптимальную смешанную стратегию, то его выигрыш равен цене игры Решение игры начинается с исключения заведомо невыгодных и дублирующих стратегий, т.е. исходную матрицу можно упростить, если исключить доминирующие столбцы, т.е. все элементы которых больше остальных и оставить доминирующие строки. После этого, упрощенную матрицу проверяют на наличие седловой точки, что позволяет сразу определить решение и цену игры. Если седловой точки нет, то переходят к определению оптимальных смешанных стратегий. Пример 1. Исследовать и решить игру, заданную матрицей Решение. 1) Проверим наличие седловой точки:
2) Найдем оптимальные смешанные стратегии. Пусть для игрока A стратегия задается вектором Тогда, на основании теоремы, при применении игроком B чистой стратегии
Аналогично, для игрока B, причем цена игры уже найдена, значит можно решить всего два уравнения
Ответ:
Так, точке При применении стратегии Соответственно, при применении стратегии Средний выигрыш Ординаты точек, лежащих на ломаной Следуя принципу максимина, получим, что оптимальное решение определяет точку M, в которой этот минимальный выигрыш достигает максимума. Ей отвечает на оси абсцисс точка По цене игры находится оптимальная стратегия для игрока B, решением системы линейных уравнений:
На этом чертеже можно показать нижнюю Если матрица имеет седловую точку, то получим следующие графики: I.
Решением игры является чистая стратегия A2 (для B-B2), т.е. P*=(0,1) и Q*=(0,1).
Решение игры соответствует т. B1 и задается векторами P*=(0,1) и Q*=(1,0). Пример 2. Решить и дать геометрическую интерпретацию игры, заданной матрицей Решение: 1) Исследуем игру на седловую точку
2) Составляем систему уравнений
Имеем Для II игрока:
Пример 3. Решить и дать геометрическую интерпретацию игры Решение: 1)
Игра имеет седловую точку. 2) Решение игры: P*=(1,0) и Q*=(1,0)
     3) 3)
из графика видно, что стратегия B2 заведомо невыгодна и A1 лучше A2. Пример 4. Найти графики решения и цену игры с матрицей (2x4)
Решение. 1) Исследуем матрицу на наличие седловой точки:
Ломаная B2MNB4 даёт нижнюю границу выигрыша, находим максимальную точку – M, в которой пересекаются чистые стратегии B2 и B1 и найдем координаты точки M как пересечение 2-х прямых B1B1 и B2B2:
Имеем Для II игрока:
Ответ: P*=(2/3,1/3), Q*=(2/3,1/3,0,0), n=5/3.
Пример 5. Сделать тоже для игры с матрицей (4x2).
Решение 1) 2)
Ломаная A2MNA3 даёт верхнюю границу проигрыша, находим максимальную точку – M, в которой пересекаются чистые стратегии A2 и A4 и найдем координаты точки M :
Имеем Для I игрока по элементам a21 и a41 строим систему:
Ответ: P*=(0,1/4,0,3/4), Q*=(5/8,3/8), n=19/4. Задания: а) Решить графическим методом матричную игру размером 2*3, б) Решить графическим методом матричную игру размером 3*2.
|



 вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную.
вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную. .
.
 и цена игры
и цена игры  или
или  игрок A получит средний выигрыш, равный цене игры, т.е.
игрок A получит средний выигрыш, равный цене игры, т.е.
 .
.
 .
. .
. Для геометрической интерпретации игры построим следующий график: в системе координат XOY отложим по оси OX отрезок
Для геометрической интерпретации игры построим следующий график: в системе координат XOY отложим по оси OX отрезок  единичной длины, каждой точке
единичной длины, каждой точке  которого будет отвечать некоторая смешанная стратегия
которого будет отвечать некоторая смешанная стратегия 

 , для которой
, для которой  , отвечает стратегия
, отвечает стратегия  , для которой
, для которой  - стратегия
- стратегия  выигрыш равен
выигрыш равен 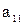 , если второй игрок применяет
, если второй игрок применяет  , если второй игрок применяет
, если второй игрок применяет  (при
(при  (при
(при 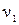 при любом сочетании стратегий
при любом сочетании стратегий  и
и  ) и стратегии
) и стратегии  , и геометрически определяется ординатой, восстановленной в точке
, и геометрически определяется ординатой, восстановленной в точке  . Аналогично, средний выигрыш при применении стратегии
. Аналогично, средний выигрыш при применении стратегии  .
.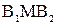 характеризуют минимальный выигрыш игрока A при использовании любой смешанной стратегии
характеризуют минимальный выигрыш игрока A при использовании любой смешанной стратегии  против стратегии
против стратегии  , а ее ордината равна цене игры
, а ее ордината равна цене игры  .
.
 и верхнюю
и верхнюю  цену игры.
цену игры.
 II.
II. .
.

 , т.е.
, т.е. 
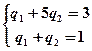 ,
, 
 3) Строим график
3) Строим график .
.

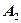

 .
. , седловой точки нет.
, седловой точки нет. 2) Строим график
2) Строим график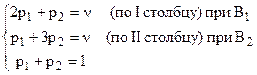


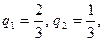 т.к. B3 и B4 не выгодно использовать, значит q3=0, q4=0.
т.к. B3 и B4 не выгодно использовать, значит q3=0, q4=0.


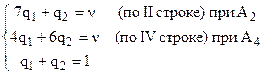



 б)
б) 
 б)
б) 
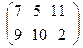 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
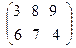 б)
б) 
 б)
б) 
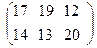 б)
б) 

 б)
б) 
 б)
б) 
 б)
б) 
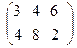 б)
б) 
 б)
б)  17) а)
17) а)  б)
б) 
 б)
б)  18) а)
18) а)  б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 