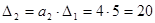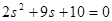ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Проверка устойчивости с помощью логарифмического критерия
Лабораторная работа №3. Критерии устойчивости САУ. Вариант 6
Выполнил: студент гр. КИП-С10(з) Коломицев А.А Проверил: Белаец Л.В.
Обнинск Дано: Передаточная функция разомкнутой системы Необходимо: 1 Получить переходный процесс и проверить устойчивость разомкнутой системы с помощью критерия Гурвица. 2 Найти полюса и нули передаточной функции разомкнутой системы и представить их графически. 3 Проверить устойчивость замкнутой системы с помощью критерия Михайлова (и следствия из него). 4 Проверить устойчивость замкнутой системы с помощью критерия Найквиста. 5 Проверить устойчивость замкнутой системы с помощью логарифмического критерия устойчивости
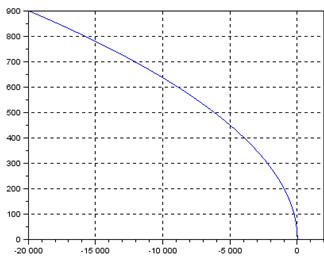
Переходный процесс
W=poly([6 4],'s','c')/poly([4 5 2],'s','c') W = 6 + 4s ---------- 4 + 5s + 2s
S=syslin('c',W) S = 6 + 4s ---------- 4 + 5s + 2s
xgrid() xtitle('Переходная функция','Время,c','Амплитуда') plot(csim("step",0:0.1:10,S))
Проверка устойчивости с помощью критерия Гурвица
Характеристическое уравнение: Все коэффициенты характеристического уравнения положительны, значит, необходимое условие устойчивости системы выполняется. Составим определители Гурвица:
det([5 0;2 4]) ans = 20.
По критерию Гурвица разомкнутая система устойчива, так как все n главных определителей матрицы коэффициентов характеристического уравнения заданной системы положительны.
Полюса и нули передаточной функции разомкнутой системы
Корни характеристического уравнения разомкнутой системы: roots(poly([4 5 2],'s','c')) ans = - 1.25 + 0.6614378i - 1.25 - 0.6614378i
plzr(S)
Система устойчива, так как вещественные части каждого из корней характеристического уравнения отрицательные. Проверка устойчивости с помощью критерия Михайлова и следствия из него
Характеристическое уравнение замкнутой системы:
poly([4,5,2],'s','c')+poly([6,4],'s','c') ans = 10 + 9s + 2s
deff('u=re(w)','u=10-2*w^2') deff('v=im(w)','v=9*w') x=re(0:0.1:100); y=im(0:0.1:100); xgrid() plot(x,y)
По критерию Михайлова замкнутая система устойчива, так как кривая Михайлова, начавшись на положительной вещественной оси и вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошла последовательно n квадрантов и ушла в бесконечность в том квадранте, номер которого соответствует показателю степени характеристического уравнения замкнутой системы (n=2).
roots(poly([10,0,-2],'w','c')) ans = 2.236068 - 2.236068
roots(poly([0,9],'w','c')) ans = 0.
plot2d(roots(poly([10,0,-2],'w','c')),[0,0],style=-1) plot2d(roots(poly([0,9],'w','c')),[0],style=-3)
Корни действительной и мнимой частей характеристического полинома перемежаются, значит согласно следствию из критерия Михайлова замкнутая система устойчива.
Проверка устойчивости с помощью критерия Найквиста
nyquist(S);
По критерию Найквиста замкнутая система устойчива, так как АФЧХ не охватывает точку с координатами (-1;j0).
Проверка устойчивости с помощью логарифмического критерия
bode(S,0.01,10)
[gm,fr]=g_margin(S) fr = [] //Частота пересечения ЛАЧХ с осью -180° gm = Inf //Запас устойчивости по амплитуде
[pm,fr2]=p_margin(S) fr2 = 0.2880736 //Частота среза pm = 124.60106 //Запас устойчивости по фазе
Вывод: Мы получили переходной процесс и проверили устойчивость разомкнутой системы с помощью критерия Гурвица. Нашли полюса и нули передаточной функции разомкнутой системы и представили их графически. Проверили устойчивость замкнутой системы с помощью критериев Михайлова (и следствия из него) Найквиста и логарифмического критерия устойчивости.
|