 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задания для аудиторной работы
Теория групп Теоретические сведения Определение 3.1. Группой называется непустое множество 1) ассоциативность: 2) существует нейтральный элемент (единица), то есть такой элемент 3) каждый элемент Группы делятся на конечные и бесконечные по числу элементов, на коммутативные и некоммутативные в соответствии со следующим определением. Определение 3.2. Группа 4) Определение 3.3. Порядком конечной группы По исторической традиции все аддитивные группы (с операцией сложения) относятся к классу коммутативных групп. Для каждого натурального Теорема 3.1. Пусть а – фиксированный элемент произвольной группы G. Пусть Определение 3.4. Группа Теорема 3.2. Пусть элемент Определение 3.5.Величина Из определения циклической группы следует, что она абелева, содержит счетное или конечное множество элементов и во втором случае имеет четкую структуру, выражаемую теоремой 3.2. Теорема 3.3. Для каждого простого числа Пусть Определение 3.6. Всякая биекция, то есть взаимно однозначное отображение Подстановку Таким образом, подстановки на Теорема 3.4. Порядок группы Пусть Определение 3.7. Циклом длиной
Цикл длиной 2 называется транспозицией. Циклы без общих элементов называются независимыми или непересекающимися. Теорема 3.5. Каждая подстановка Теорема 3.6. Каждая подстановка Пример 3.1.Разложить в произведение циклов и транспозиций подстановку
Решение.
Разложение подстановки в произведение транспозиций неоднозначно.
Определение 3.8. Подстановка Задания для аудиторной работы Задание 3.1.Привести десять примеров групп. Почему вы считаете, что это действительно группа? Это абелева группа? Ваша группа конечна? Задание 3.2. Определить, является ли группой относительно операции умножения множество Решение. 1) 2) нейтральный элемент 3) для каждого
Следовательно, Задание 3.3. Выяснить, является ли группой множество всех положительных вещественных чисел с бинарной алгебраической операцией возведения в степень? Решение. Нет, потому что данная операция не ассоциативна. Например, Задание 3.4. Разложить в произведение циклов и транспозиций подстановку
Решение. Подстановка Задание 3.4. Вычислить произведение Решение. Задание 3.5.Вычислить произведение циклов и транспозиций
Решение.
Задание 3.6.Выписать циклическую группу, порожденную подстановкой
Решение. Согласно теореме 3.2 группа Задание 3.7. Выяснить, обратима ли матрица Решение.Найдем определитель матрицы А. Задание 3.8. Выписать циклическую группу, порожденную матрицей из предыдущего задания, и указать ее порядок. Решение. Задание 3.9.Является ли циклической аддитивная группа: а) вещественных чисел? б) рациональных чисел? |



 с одной определенной на нем бинарной алгебраической операцией, относительно которой выполняются следующие свойства:
с одной определенной на нем бинарной алгебраической операцией, относительно которой выполняются следующие свойства: для любых
для любых  ;
; , что
, что  для каждого
для каждого  ;
; имеет обратный, то есть такой элемент
имеет обратный, то есть такой элемент 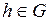 , что
, что  ( в этом случае пишут
( в этом случае пишут  ).
). называется коммутативной или абелевой, если определенная в ней операция (в дополнение к свойствам 1) – 3)) обладает свойством
называется коммутативной или абелевой, если определенная в ней операция (в дополнение к свойствам 1) – 3)) обладает свойством 
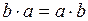 для всех
для всех 
 .
.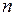 найдется коммутативная конечная группа порядка
найдется коммутативная конечная группа порядка  Например,
Например, 
 – множество всевозможных степеней элемента а. Тогда
– множество всевозможных степеней элемента а. Тогда  группа, причем абелевая.
группа, причем абелевая. из теоремы 3.1 называется циклической группой, порожденной элементом
из теоремы 3.1 называется циклической группой, порожденной элементом  .
. обладает свойством:
обладает свойством:  для некоторого целого
для некоторого целого  для всех целых
для всех целых  Тогда циклическая группа
Тогда циклическая группа 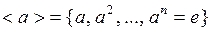 .
. Если же для элемента
Если же для элемента  такого
такого  имеет бесконечный порядок.
имеет бесконечный порядок. множество всех ненулевых классов из кольца классов вычетов
множество всех ненулевых классов из кольца классов вычетов  образует группу
образует группу  относительно операции умножения, причем эта группа является циклической.
относительно операции умножения, причем эта группа является циклической. – конечное множество из
– конечное множество из  .
. ,
, 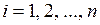 , удобно изображать в наглядной развернутой форме в виде двустрочной таблицы:
, удобно изображать в наглядной развернутой форме в виде двустрочной таблицы:  . В этой таблице каждый
. В этой таблице каждый  -й столбец четко указывает в какой элемент
-й столбец четко указывает в какой элемент  преобразуется элемент
преобразуется элемент 
 . Подстановки перемножаются в соответствии с общим правилом композиции отображений:
. Подстановки перемножаются в соответствии с общим правилом композиции отображений:  Чаще всего
Чаще всего  , то есть композиция подстановок не обладает свойством коммутативности. Очевидно, тождественная подстановка
, то есть композиция подстановок не обладает свойством коммутативности. Очевидно, тождественная подстановка 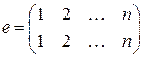 играет роль единицы относительно композиции подстановок. Как известно, композиция отображений является ассоциативной операцией, поэтому и композиция подстановок ассоциативна. Каждая подстановка – обратимая операция. Чтобы найти для подстановки
играет роль единицы относительно композиции подстановок. Как известно, композиция отображений является ассоциативной операцией, поэтому и композиция подстановок ассоциативна. Каждая подстановка – обратимая операция. Чтобы найти для подстановки  обратную подстановку
обратную подстановку  достаточно в таблице
достаточно в таблице  переставить строки местами, а затем столбцы упорядочить по возрастанию элементов первой строки.
переставить строки местами, а затем столбцы упорядочить по возрастанию элементов первой строки.
 равен
равен  .
. произвольная подстановка из
произвольная подстановка из  Из двустрочной таблицы, задающей
Из двустрочной таблицы, задающей  выбросим столбцы с одинаковыми элементами.
выбросим столбцы с одинаковыми элементами. называется подстановка вида
называется подстановка вида .
. ,
,  , является произведением независимых циклов длиной
, является произведением независимых циклов длиной  . Это разложение в произведение определено однозначно с точностью до порядка следования циклов.
. Это разложение в произведение определено однозначно с точностью до порядка следования циклов.


 всех комплексных чисел, имеющих единичный модуль.
всех комплексных чисел, имеющих единичный модуль. для любых комплексных чисел;
для любых комплексных чисел; для любого комплексного числа;
для любого комплексного числа; по условию
по условию  то есть
то есть  поэтому обратным элементом для
поэтому обратным элементом для 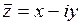 :
:
 действительно является группой.
действительно является группой. , а
, а 
 . Определить четность
. Определить четность 
 перемещает 1 в 7, 7 в 2, 2 в 4, 4 в 1. В соответствии с определением 3.8 подстановка, действующая на элементы 1, 7, 2, 4 по данному правилу, а на все остальные – тождественно, называется циклом длиной 4. В соответствии с определением 3.8 данный цикл кратко записывают так: (1724). Также
перемещает 1 в 7, 7 в 2, 2 в 4, 4 в 1. В соответствии с определением 3.8 подстановка, действующая на элементы 1, 7, 2, 4 по данному правилу, а на все остальные – тождественно, называется циклом длиной 4. В соответствии с определением 3.8 данный цикл кратко записывают так: (1724). Также  указывает на то, как
указывает на то, как  . Поскольку цикл, состоящий из одного элемента, совпадает
. Поскольку цикл, состоящий из одного элемента, совпадает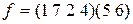 – произведение циклов. Отсюда получаем разложение подстановки
– произведение циклов. Отсюда получаем разложение подстановки  . Как видим,
. Как видим,  четная подстановка.
четная подстановка. для
для  и
и 
 . Тогда
. Тогда  .
.


 .
. ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 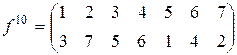 ;
;  ;
;  .
. порядка 12.
порядка 12. с элементами из кольца классов вычетов
с элементами из кольца классов вычетов  .
. . Следовательно, матрица А обратима.
. Следовательно, матрица А обратима. . Следовательно,
. Следовательно,  группа порядка 2.
группа порядка 2.